帶形狀參數的三次三角Hermite插值樣條曲線

李軍成，鐘月娥，謝淳

湖南人文科技學院數學系，湖南婁底 417000

帶形狀參數的三次三角Hermite插值樣條曲線

李軍成，鐘月娥，謝淳

湖南人文科技學院數學系，湖南婁底 417000

給出了一種帶形狀參數的三次三角Hermite插值樣條曲線，具有標準三次Hermite插值樣條曲線完全相同的性質。給定插值條件時，樣條曲線的形狀可通過改變形狀參數的取值進行調控。在適當條件下，該樣條曲線對應的Ferguson曲線可精確表示橢圓、拋物線等工程曲線。通過選擇合適的形狀參數，該插值樣條曲線能達到C2連續，而且其整體逼近效果要好于標準三次Hermite插值樣條曲線。

三次Hermite插值樣條；三次三角Hermite插值樣條；形狀參數；逼近

1 引言

三次Hermite插值樣條是工程中較為常見的一種構造插值曲線的方法，但是插值條件給定時，標準三次Hermite插值樣條存在形狀無法修改、僅滿足C1連續、不能精確表示常見工程曲線等缺陷。帶有參數的有理形式的Hermite插值樣條[1-8]不僅具有標準三次Hermite插值樣條相似的性質，而且其形狀可通過改變參數的取值進行調節，在一定條件下，這些帶參數的有理Hermite插值樣條還能達到C2連續，但這些樣條卻不能精確表示一些常見的工程曲線。近年來，基于三角函數的幾何造型方法得到了廣泛的研究，一些學者對三角多項式樣條也作了有益的探討[9-13]，其中謝進等人[12-13]針對帶參數的有理Hermite插值樣條不能精確表示工程中常見的曲線這一缺陷，提出了一種帶參數的有理三次三角Hermite插值樣條，和一般的有理樣條一樣，其形狀可通過形狀參數進行調控，另外在適當的條件下，該樣條對應的Ferguson曲線還能精確表示工程中一些常見的曲線。

無論是一般的有理Hermite插值樣條，還是有理三角Hermite插值樣條，由于都是采用有理形式構造樣條，因此其表達式變得復雜，計算量也隨之變得較大。為此，本文提出了一種帶形狀參數的三次三角多項式Hermite插值樣條曲線，該樣條曲線不僅與標準三次Hermite插值樣條曲線具有相同的性質，而且可以利用形狀參數對樣條的形狀進行調控。給定插值條件，當參數取合適值時，該樣條曲線可達到C2連續，且整體逼近效果好于標準三次Hermite插值樣條。另一方面，在合適的條件下，該樣條曲線對應的Ferguson曲線還可以精確表示橢圓與拋物線。由于所提出的三角Hermite插值樣條避免了使用有理形式，其表達式較為簡潔，計算量也相對較小，從而為插值曲線曲面的構造提供了一種新方法。

2 三次三角Hermite基函數

一般地，對于給定的節點：

下面利用{1，sin t，cos t，sin2t，sin3t，cos3t}取代標準三次Hermite基函數中的{1，t，t2，t3}，構造一種帶形狀參數的三次三角Hermite基函數。

定義1對任意給定的任意實數λi，0≤t≤1，下列4個關于t的函數：

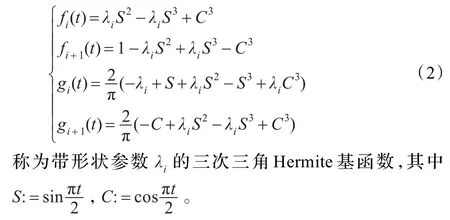
經簡單計算可知，擬三次雙曲Hermite基函數滿足下列性質：

（1）端點性：對任意的參數λi，有：

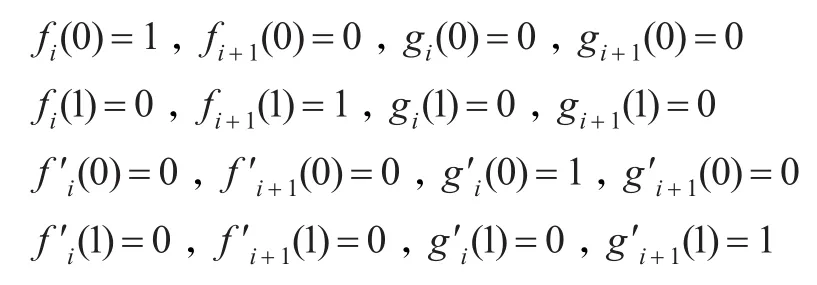
且有fi(t)+fi+1(t)=1，gi(t)=-gi+1(1-t)。

上述結論表明，三次三角Hermite基函數與標準Hermite基函數具有完全相同的性質，但與之不同的是，三次三角Hermite基函數帶有參數λi，當參數λi取不同值時可得到不同的三次三角Hermite基函數。

（2）關于參數λi的單調性：固定變量t，求fi(t)，fi+1(t)，gi(t)，gi+1(t)分別關于參數λi的導數，記為d f0，d f1，d g0，d g1，則有：

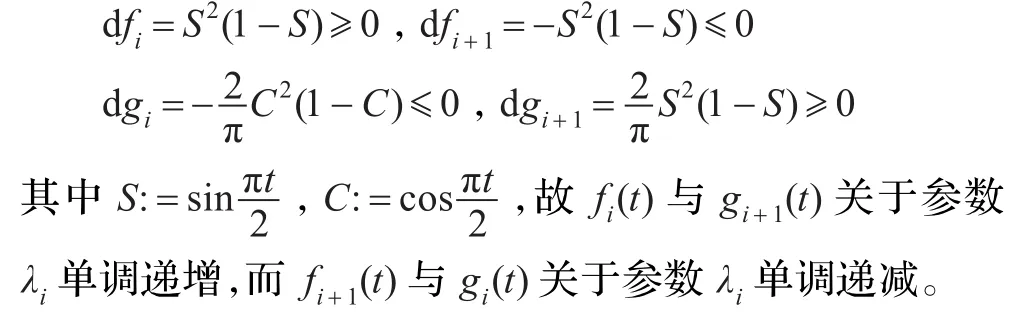
3 三次三角Ferguson曲線

由三次三角Hermite基函數的性質可知，基于該組基函數可作兩點的Hermite插值，因此可定義相應的Ferguson曲線。

定義2對任意給定的任意實數λi，0≤t≤1，稱：

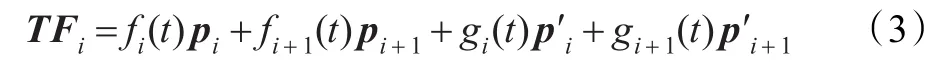
為帶形狀參數λi的三次三角Ferguson曲線，其中pi+j與p′i+j(j=0，1)分別為兩個插值端點及其切矢，fi+j(t)與gi+j(t)(j=0，1)為三次三角Hermite基函數。

顯然，三次三角Ferguson曲線與標準三次Ferguson曲線具有相同的插值性，但與之不同的是，三次三角Ferguson曲線帶有形狀參數λi，當兩個插值端點及其切矢給定時，利用形狀參數λi可對曲線的形狀進行調控。在適當條件下，三次三角Ferguson曲線可以精確表示直線段、橢圓弧與三次拋物線弧。

4 三次三角Hermite插值樣條曲線

4.1 樣條曲線的定義

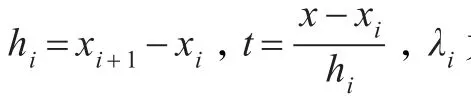
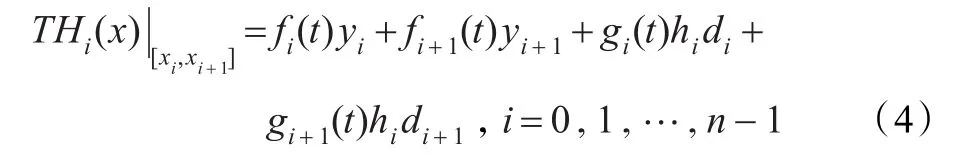
為區間[a，b]上關于分劃?的分段三次三角Hermite插值樣條曲線，其中fi(t)，fi+1(t)，gi(t)與gi+1(t)為三次三角Hermite基函數。

容易驗證，由式（4）定義的三次三角Hermite插值樣條曲線滿足：

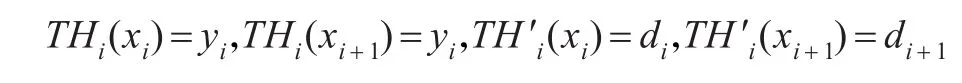
上述結論表明，當插值條件給定時，三次三角Hermite插值樣條曲線不僅滿足C1連續，而且其形狀還可通過修改參數λi的取值進行局部或整體調控，這相對于形狀無法改變的標準三次Hermite插值樣條曲線而言，給設計人員的交互式設計帶來了方便。

例1給定數據：

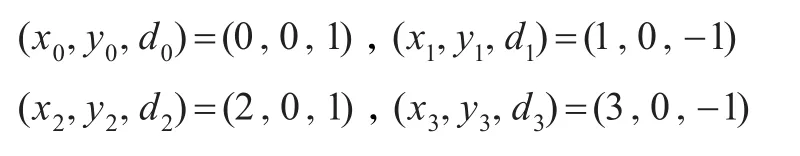
則可繪制出由3段三次三角Hermite插值樣條曲線構成的整條C1連續曲線，并可通過修改參數λi(i=0，1，2)的取值實現對整條曲線的局部或整體調控。圖1為形狀參數λ1對曲線進行局部調控的情形，這里取λ0=λ2=1，粗實線對應λ1=-0.5，虛線對應λ1=0，細實線對應λ1=0.5。圖2為形狀參數對曲線進行整體調控的情形，這里取λi=λ(i=0，1，2)，其中粗實線對應λ=0.5，細實線對應λ=1.5，虛線為標準三次Hermite插值樣條曲線。

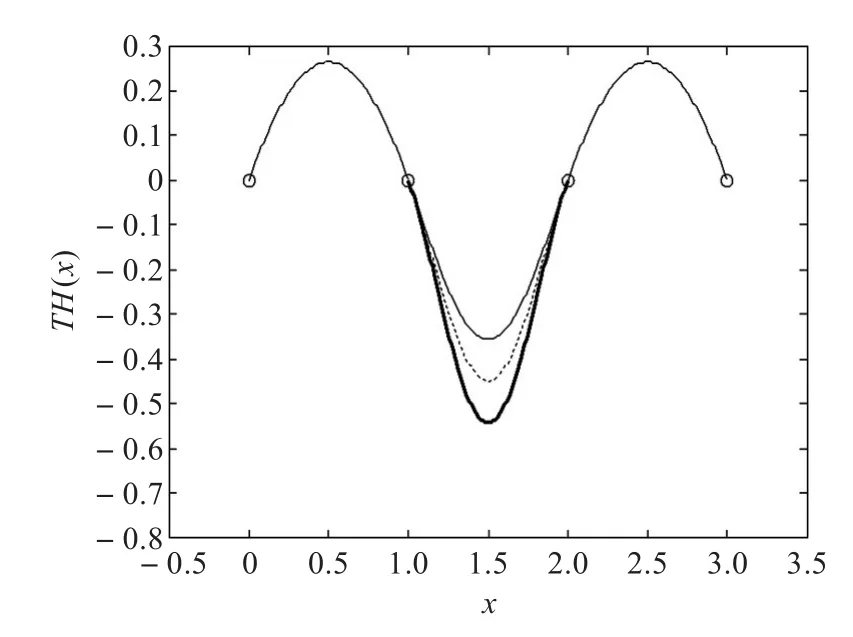
圖1 插值樣條曲線的局部調控

另外，當給定插值條件時，標準三次Hermite插值樣條曲線僅滿足C1連續，而在適當條件下，三次三角Hermite插值樣條曲線可達到C2連續。事實上，令

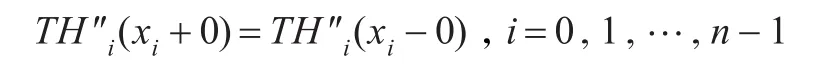
可得如下的連續性方程：

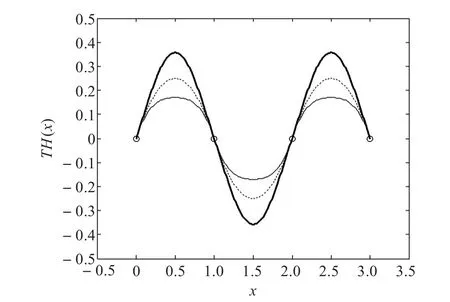
圖2 插值樣條曲線的整體調控

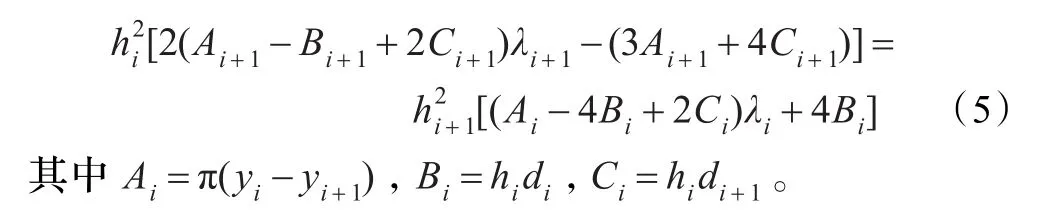
式（5）稱為三次三角Hermite插值樣條的C2連續性約束條件，即當形狀參數λi(i=0，1，…，n-1)滿足式（5）時，三次三角Hermite插值樣條滿足C2連續。在實際計算中，可適當地指定[x0，x1]上的初始參數λ0，然后可由λ0通過式（5）確定λ1，再由λ1通過式（5）確定λ2，依次類推，逐段構造出區間[a，b]上C2連續的整條三次三角Hermite插值樣條曲線。

需要說明的是，在實際應用中，給定初始參數λ0后，由于通過式（5）計算所得的其他參數λi都是近似值，因此當曲線的段數較大時，可能會使得誤差的累積較大，后面相鄰曲線段的C2連續性就不能保證。此時，可將給定的數據劃分為若干部分，并按照上述方法分別對每個部分的數據構造C2連續的曲線，然后再利用Hermite插值方法將各部分曲線構造成整條C2連續的曲線。

例2給定數據點如下：

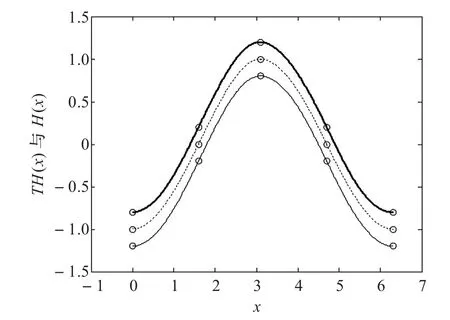
圖3 C2連續的樣條曲線（粗實線）

若指定初始形狀參數λ0=0.000 0，由式（5）依次計算得λ1=1.015 3，λ2=6.063 5，λ3=0.956 5，利用所得參數可繪制出一條C2連續的三次三角Hermite插值樣條曲線，如圖3中的粗實線。在圖3中，細實線為所有參數取λi=1時的三次三角Hermite插值樣條曲線TH(x)，虛線為標準的三次Hermite插值樣條曲線H(x)，此時三次三角Hermite插值樣條曲線和標準三次Hermite插值樣條曲線僅滿足C1連續。由于三條曲線幾乎重合，為了區別觀察，將圖8中的粗實線整體上升了0.2個單位，而細實線則整體下降0.2個單位。

4.2 樣條曲線的逼近性

下面討論參數的選擇對三次三角Hermite插值樣條曲線對被插函數逼近程度的影響，這里僅與標準三次Hermite插值樣條曲線進行比較。為此，首先給出一種刻畫整體逼近效果的定義。

定義4設在區間[a，b]上構造的整條標準三次Hermite插值樣條曲線為H(x)，三次三角Hermite插值樣條曲線為TH(x)，被插函數為f(x)。記相對誤差：

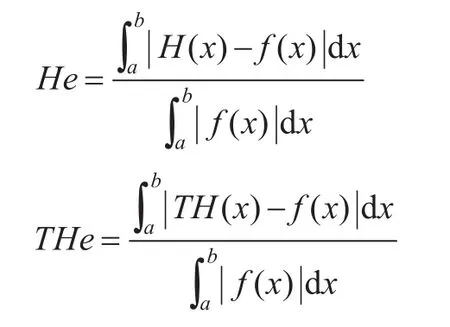
則當THe＜He時，稱TH(x)比H(x)在[a，b]對f(x)的整體逼近效果好。

例3設被插函數分別為f(x)=4-2 sin x，采用三次三角Hermite插值樣條曲線對f(x)進行插值逼近，給定的插值條件及各區間上參數λi的取值如表1所示。

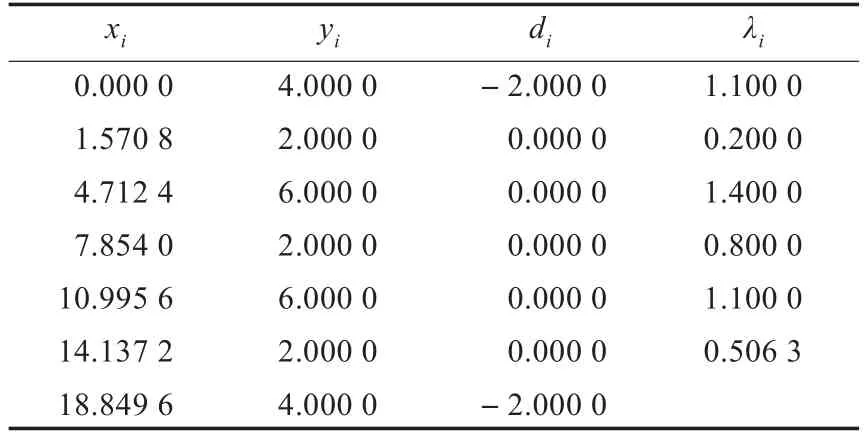
表1 給定的插值條件及各區間上參數的取值

分別采用三次三角Hermite插值樣條曲線TH(x)與標準三次Hermite插值樣條曲線H(x)對被插函數f(x)進行插值逼近的圖形如圖4所示。由于TH(x)（粗實線部分）、H(x)（細實線部分）和f(x)（短虛線部分）幾乎重合，為了便于區別觀察，將圖4中的TH(x)整體上升了1個單位，H(x)則整體下降了1個單位。

經計算，采用TH(x)對f(x)進行插值逼近的誤差值THe=0.000 393 68，而采用H(x)對f(x)進行插值逼近的誤差值He=0.039 700 10。由此可知，當形狀參數取適當的值時，采用三次三角Hermite插值樣條曲線逼近的誤差值比標準三次Hermite插值樣條曲線小得多，這也表明在形狀參數取值適當時，三次三角Hermite插值樣條曲線比標準三次Hermite插值樣條曲線相對于被插函數具有更好的整體逼近性。

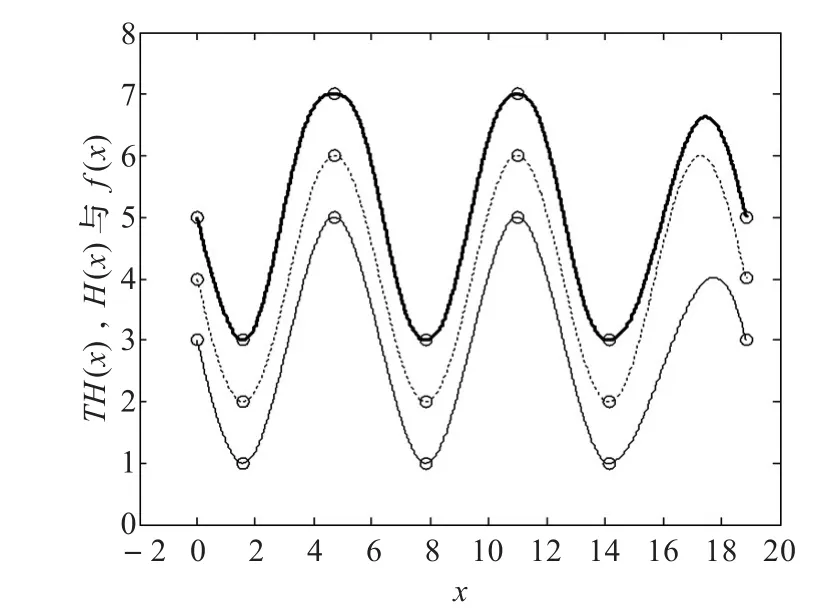
圖4 兩種插值樣條曲線與被插函數

5 結束語

本文提出了一種帶形狀參數的三次三角Hermite插值樣條曲線，該曲線具有以下幾個優點：（1）每段插值樣條曲線只帶一個形狀參數，曲線的形狀可通過改變參數的取值進行調控，方便實用。（2）在適當條件下，該曲線對應的Ferguson曲線可精確表示橢圓、拋物線等工程曲線。（3）當形狀參數取值適當時，該曲線可達到C2連續，且整體逼近效果好于標準三次Hermite插值樣條曲線。（4）相對于有理三角插值樣條而言，該曲線避免了有理形式，因此其表達式變得較為簡潔，計算量也較小。另外，本文提出的插值樣條曲線可推廣至曲面形式，將另文討論。

[1]Hall C A，Meyer W W.Optimal error bounds for cubic spline interpolation[J].Journal of Approximation Theory，1976，16（2）：105-122.

[2]Duan Q，Djidjeli K，Price W G，et al.Rational cubic spline based on function values[J].Computer and Graphics，1998，22（4）：479-486.

[3]Duan Q，D jidjeli K，Price W G，et al.The approximation properties of some rational cubic splines[J].International Journal of Computer Mathematics，1999，72（2）：155-166.

[4]Sarfraz M.Cubic spline curves with shape control[J].Computer and Graphics，1994，18（5）：707-713.

[5]Duan Q，Liu A K，Cheng F H.Constrained interpolation using rational cubic spline with linear denominators[J]. Korean Journal of Computational and Applied Mathematics，1999，6（1）：203-215.

[6]劉愛奎，段奇，單滬軍，等.加權有理三次插值的逼近性質及其應用[J].高校應用數學學報：A輯，2000，15（2）：211-218.

[7]來翔，劉愛奎，段奇.一類具有線性分母的有理插值樣條的逼近問題[J].工程數學學報，2002，19（1）：94-98.

[8]謝進，檀結慶，李聲鋒.有理三次Hermite插值樣條及其逼近性質[J].工程數學學報，2011，28（3）：385-392.

[9]王文濤，汪國昭.帶形狀參數的三角多項式均勻B樣條[J].計算機學報，2005，28（7）：1192-1198.

[10]鄔弘毅，陳曉彥.多形狀參數的三次非均勻三角多項式曲線[J].計算機輔助設計與圖形學學報，2006，18（10）：1599-1606.

[11]尹池江，檀結慶.帶多形狀參數的三角多項式均勻B樣條曲線曲面[J].計算機輔助設計與圖形學學報，2011，23（7）：1131-1138.

[12]謝進，檀結慶，李聲鋒，等.有理三次三角Hermite插值樣條曲線及其應用[J].計算機工程與應用，2010，46（5）：7-9.

[13]謝進，檀結慶，劉植，等.一類帶參數的有理三次三角Hermite插值樣條[J].計算數學，2011，22（2）：125-132.

LI Juncheng,ZHONG Yue’e,XIE Chun

Department of Mathematics,Hunan Institute of Humanities,Science and Technology,Loudi,Hunan 417000,China

A class of cubic trigonometric Hermite interpolating splines curves with shape parameters is presented in this paper, which inherits the same properties of the standard cubic Hermite interpolating splines. For given interpolating conditions, the shape of the proposed splines curves can be adjusted by changing the values of the parameters. In proper conditions, the corresponding Ferguson curve can be used to represent some engineering curves exactly, such as ellipse and parabola. By selecting proper shape parameters, the proposed interpolating splines curves could satisfy C2 continuous and approximate the interpolated functions better than the standard cubic Hermite interpolating splines curves.

cubic Hermite interpolating splines;cubic trigonometric Hermite interpolating sp lines;shape parameters; approximation

LI Juncheng,ZHONG Yue’e,XIE Chun.Cubic trigonoMetric Hermite interpolating splines curves with shape parameters.Computer Engineering and Applications,2014,50（17）：182-185.

A

TP391

10.3778/j.issn.1002-8331.1209-0067

湖南省教育廳資助科研項目（No.14B099）。

李軍成（1982—），男，在職博士研究生，講師，研究領域為計算機輔助幾何設計、圖像處理；鐘月娥（1980—），女，講師，研究方向為計算機輔助幾何設計；謝淳（1982—），女，講師，研究方向為計算機輔助幾何設計。E-mail：lijuncheng82@126.com

2012-09-11

2012-12-20

1002-8331（2014）17-0182-04

CNKI網絡優先出版：2012-12-24,http://www.cnki.net/kcms/detail/11.2127.TP.20121224.1515.003.htm l