基于混合蛙跳算法的協同空戰火力分配

張凱，周德云，潘潛

西北工業大學電子信息學院，西安 710129

基于混合蛙跳算法的協同空戰火力分配

張凱，周德云，潘潛

西北工業大學電子信息學院，西安 710129

針對超視距多機協同空戰中的火力分配（WTA）問題，建立了協同空戰火力分配的數學模型，提出了采用混合蛙跳算法（SFLA）來求解協同空戰火力分配問題，根據無約束化的編碼方式，結合交叉、變異的遺傳操作，提高了算法的收斂速度以及全局搜索能力，能有效避免陷入局部最優。仿真結果表明，所提出的混合蛙跳算法在解決協同空戰火力分配問題中具有高效可行性。

協同空戰；火力分配；混合蛙跳算法；遺傳算子

1 引言

隨著機載火控系統的快速發展，超視距協同空戰已成為現代空戰的主要形式，火力分配作為必不可少的決策支持，一直是研究的熱點[1]。Lloyd和W itsenhausen已證明了WTA問題是NP完全問題[2]，針對該問題，目前已有多種算法，如拍賣算法[3]、混合粒子群算法[4-6]、蟻群算法[7-8]、遺傳算法[9]等，以上算法均已應用于火力分配并取得顯著的成果。

在以上研究的基礎上，本文提出了一種混合蛙跳算法求解協同多目標空戰決策問題。作為一種新的仿生學智能優化算法，蛙跳算法結合了基于模因進化的模因演算法（M emetic A lgorithm，MA）和基于群體行為的粒子群算法（Particle Swam optimization，PSO）的優點，調整參數少，收斂速度快，全局尋優能力強[10]。仿真結果表明了該算法在解決協同多目標空戰決策問題中的有效性。

2 協同空戰火力分配數學模型

設在多機系統攻擊多目標的超視距空戰中，我方的空戰編隊有n架飛機，每架飛機載有ki枚導彈，共有k1+k2+…+kn=k枚導彈；所要攻擊的敵機數目為m架，每架敵機的威脅系數為ωh，h=1，2，…，m。其中第i枚導彈對第j架敵機的毀傷概率為pij，i=1，2，…，k，j=1，2，…，m。

引入火力分配的決策矩陣[11]：

xij為決策變量，xij=1表示分配了第i枚導彈攻擊第j架敵機，否則xij=0。

則協同空戰火力分配數學模型可描述為：尋求一組解X，滿足以下目標函數和約束條件：

目標函數：

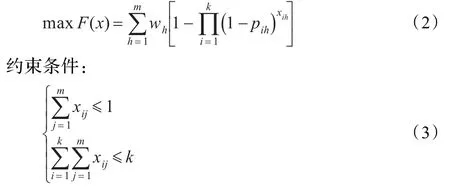
其中，第一個約束條件表示一枚導彈只能用于打擊一個目標，第二個約束條件表示所能使用的導彈數量不超過k個。

3 蛙跳算法

蛙跳算法（Shuffled Frog Leaping A lgorithm，SFLA）由Eusuff和Lansey為解決組合優化問題于2003年提出[12]，作為一種新的仿生學智能優化算法，該算法具有調整參數少、收斂速度快、有效避免局部最優解的特點。目前混合蛙跳算法主要應用于解決多目標優化問題，如資源分配、作業調度、流程安排等工程實際應用問題[13-14]。

作為一種后啟發式群體進化算法，蛙跳算法的思想是：濕地中的一群青蛙通過尋找不同的石頭進行跳躍去找到食物較多的地方。青蛙具有自己的文化，每只青蛙的文化被定義為問題的一個解，個體之間通過文化的交流實現信息的交換。濕地的整個青蛙群體被分為不同的子群體，在子群體中的每個個體通過自己的文化影響著其他個體，也受其他個體的影響，并隨著子群體的進化而進化，執行局部搜索策略。當子群體進化到一定階段以后，各子群體之間再進行文化的交流實現子群體間的混合運算。重復上述過程，直到滿足設置的截止條件為止。

SFLA算法的數學模型可以表示為：首先，隨機初始化生成解空間為S維、規模為N的初始種群P= {X1，X2，…，XN}，第i只蛙表示問題的一個解Xi=[xi1，xi2，…，xiS]。將初始種群中蛙的個體按適應值降序排列，并將種群中具有最優適應值的個體記為Xg。然后將整個種群分為m個模因組，每個模因組含有n只蛙，即N=n×m，分配方法為：第1只蛙分入第1模因組，第2只蛙分入第2模因組，…，第m只蛙分入第m模因組，第m+1只蛙分入第1模因組，…，依次類推。第k個模因組的蛙的集合Ak可表示為[15]：

將每個模因組中的最優適應值個體和最劣適應值個體記為Xb、Xw，然后在每個模因組中根據蛙跳規則執行局部搜索策略：

式中，rand()表示（0，1）之間的隨機數，Dmax表示蛙每次跳躍步長的最大值。在經過更新后，如果得到的優于原來的Xw，則取代原模因組中的Xw；如果沒有改進，則用Xg取代Xb，再按式（5）與式（6）執行局部搜索過程，如果仍沒有改進，則隨機產生一個新蛙直接取代原Xw。重復上述局部搜索過程iN次，然后將整個蛙群重新混合并排序和劃分基因組，再進行局部搜索，如此反復，直到滿足設定的截止條件為止，如適應度達到期望值或達到混合迭代次數im。

4 求解火力分配問題的混合SFLA算法

協同多目標空戰火力分配的數學模型作為帶有一定約束條件的非線性0-1整數規劃問題，若按基本SFLA算法來求解，其步長的速度向量難以表達。故本文在一種無約束化的編碼方式上，借鑒遺傳算法的交叉、變異思想，采用遺傳-蛙跳混合算法來解決空戰火力分配問題。

4.1 解的編碼

在混合SFLA算法中，對解的位置需要結合實際問題進行編碼。本文采用了一種基于實數的編碼方式，此編碼方式不僅用粒子位置代表一種導彈-目標分配的決策方案，而且還滿足模型中所有約束條件的要求，從而實現了原規劃問題的無約束轉化。

由上述設計第i個載機平臺的火力策略空間：

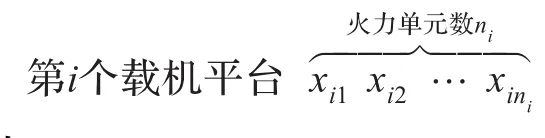
其中，xir∈0，1，…，m;r∈1，2，…，ni。當xir=h時，表示第i個載機平臺的第r枚導彈用于摧毀第h個目標，當xir=0時，表示第i個載機的第r個武器單元沒有使用。以上是第i個載機平臺決策序列的編碼，編碼長度為ni，其他平臺以此類推。

4.2 個體更新策略

首先，選出整個種群中最優適應值個體Pg，每個模因組中的最優適應值個體Pb、最劣適應值個體Pw。然后將Pb和Pw進行交叉操作，比較新產生的兩個個體與Pw的適應值，如有比Pw適應度高的個體，就用較優適應值的個體替代Pw。否則用Pg代替Pb與Pw進行交叉操作，如果產生的個體仍不優于Pw，則對Pw進行變異操作，并用產生的新個體直接替代Pw。具體的交叉、變異操作策略如下：

交叉操作：由解的編碼方式可知，編碼長度等于我機編隊的火力單元總數k，所以粒子X與粒子Y均是長度為k的實數序列。生成一個長為k的0-1隨機序列，在“1”對應的位置上將粒子X與粒子Y進行交換，“0”所在的位置則不進行操作，從而產生新粒子X'、Y'。

變異操作：變異操作與交叉操作類似，首先生成一個長為k的0-1隨機序列，在“1”所在的位置上對粒子X進行變異操作，“0”所在的位置上則不進行操作。

4.3 混合SFLA算法流程

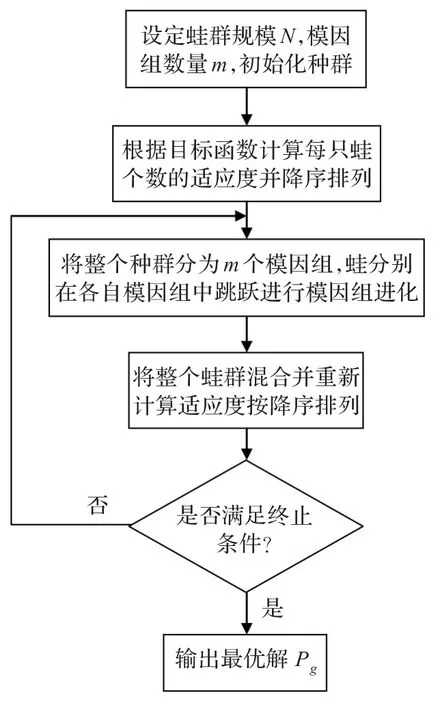
圖1 蛙跳算法總流程

5 仿真分析

為了測試混合SFLA算法處理協同多目標攻擊空戰決策問題的性能，引入文獻[4]中所用的作戰想定，設我方戰機編隊與敵機編隊在超視距條件下進行空戰，我方戰機數量為4架，每架飛機上均掛載4枚導彈，共探測到聯合攻擊區內的10架敵機，我方戰機編隊采用協同空戰戰術。

各導彈對各目標的毀傷概率矩陣為：

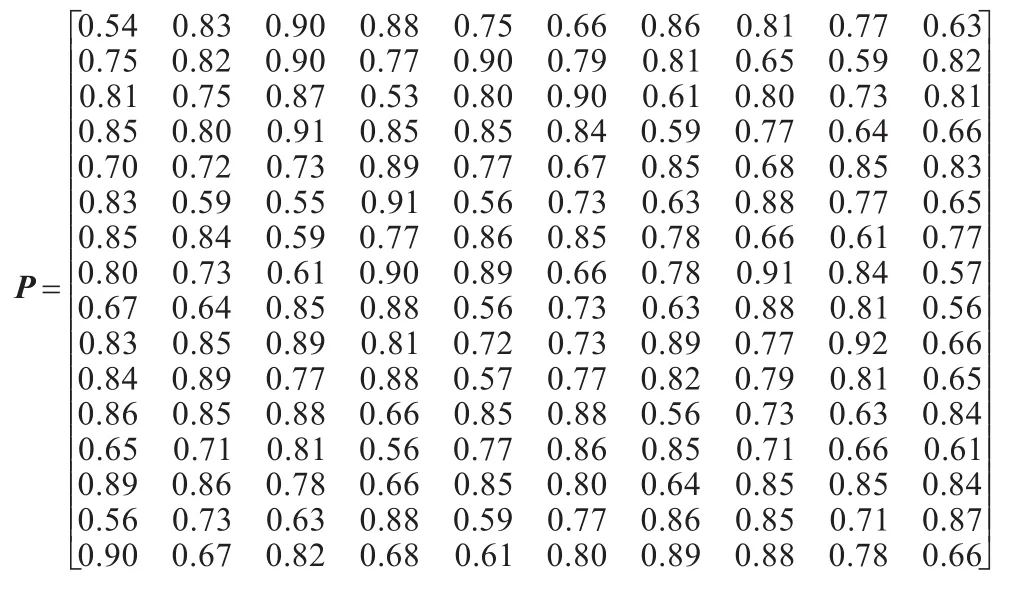
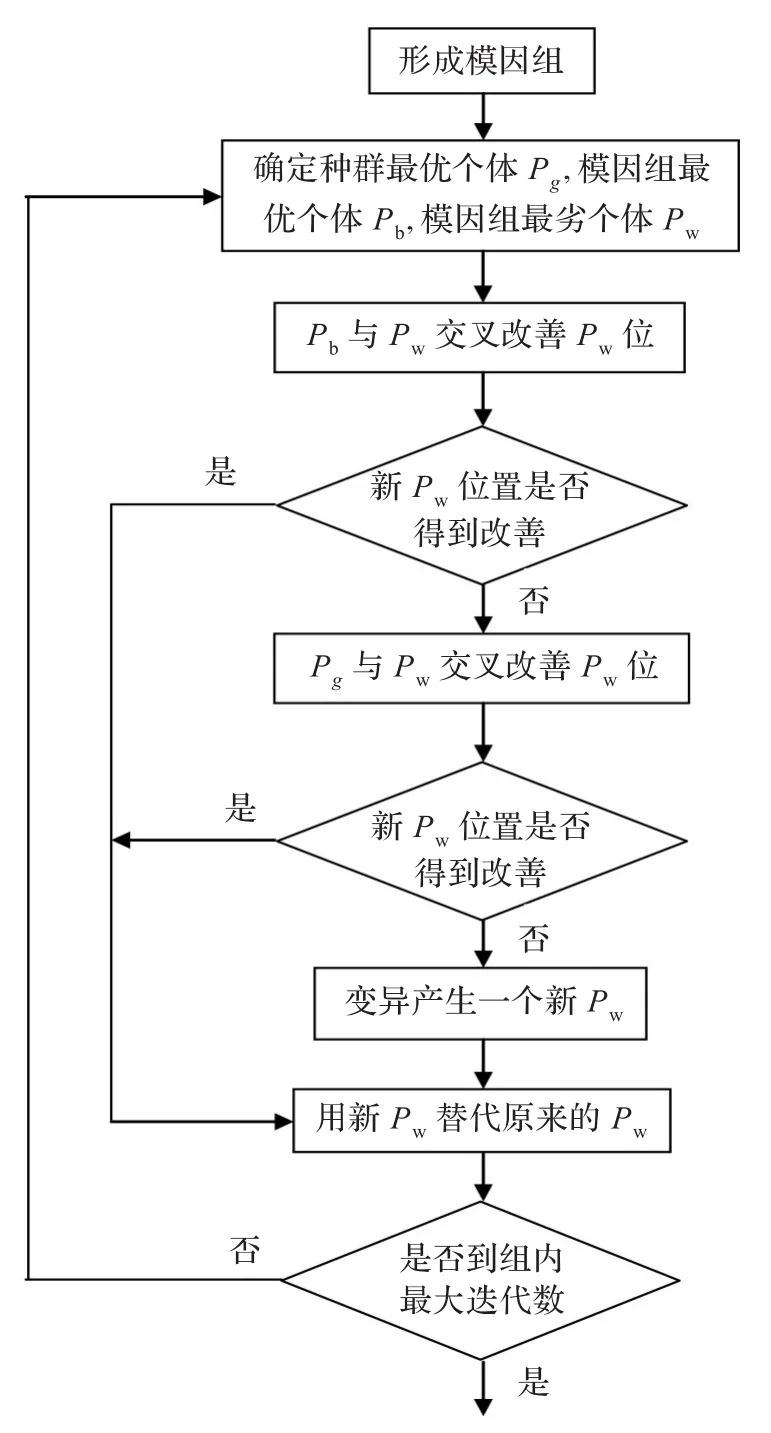
圖2 模因組進化流程

各目標的威脅權重矩陣為：

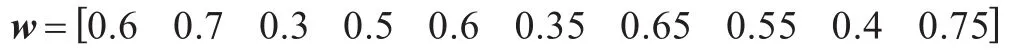
在本文所采用的GA-SFLA算法中，種群規模取為100個，模因組數目為5個，每個模因組規模為20個。在這樣的情況下，使用GA-SFLA算法和SA-DPSO算法分別對該火力分配問題進行優化求解。所得的最優適應值變化情況見圖3。

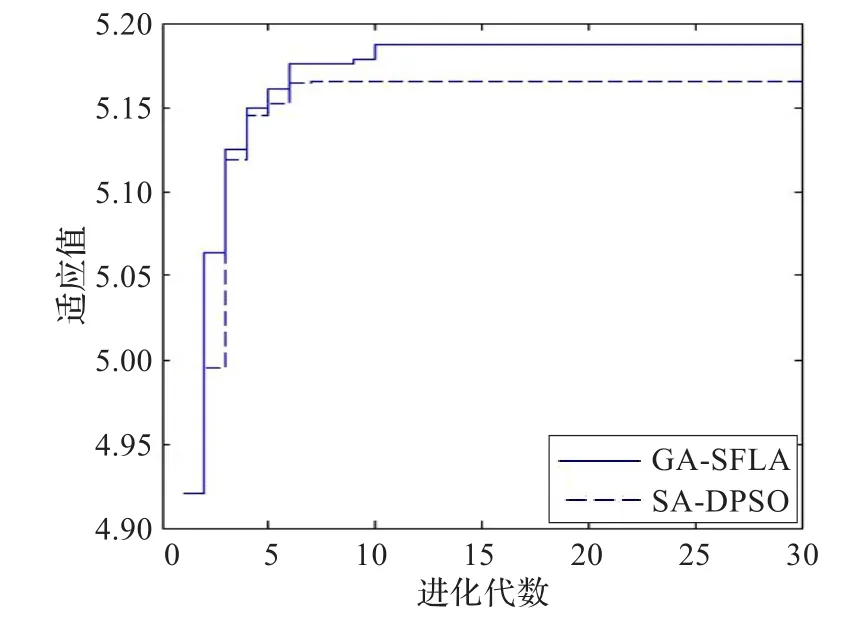
圖3 最佳適應值的變化曲線

最優分配情況如下：

通過比較可知，混合SFLA算法不但可以在設定的代數中找到最優解，而且能夠有效地避免局部最優。而SA-DPSO算法不僅收斂速度慢于混合SFLA算法，且在迭代過程中會陷入局部最優解。此外，考慮到火力分配的實時性問題，從算法的效率上來看，GA-SFLA的粒子更新只需對每個模因組的最后一個粒子進行操作，將更新后的該粒子根據適應值排序重新插入到模因組中，整個算法具有并行性且設置參數少。而SA-DPSO算法是一種兩層的串行結構，DPSO的一次優化結果作為SA的初始種群，SA經M etropolis抽樣過程得到的解又成為下一次進化的初始種群，過程復雜且涉及的動態參數較多，不利于大規模問題的快速求解。這說明本文提出的混合SFLA算法在解決協同空戰火力分配問題上是快速有效的。

6 結論

本文建立了協同空戰火力分配數學模型，引入的編碼方式將原模型轉化成為無約束優化問題，且不增加問題的復雜性。提出了一種混合SFLA算法對模型進行求解，在求解過程中，充分利用了群智能的信息（種群最優、模因組最優和模因組最劣）和智能算法的個體智能（交叉、變異），且各模因組進化具有高度的并行性，體現了分布式計算的高效率。仿真結果表明，提出的混合SFLA算法是快速有效的。

[1]蔡懷平，陳英武.武器-目標分配（WTA）問題研究進展[J].火力與指揮控制，2006，31（12）：11-15.

[2]Lloyd S P，H S W.Weapons allocations is NP-complete[C]// Proceedings of the 1986 Summer Conference on Simulation，Reno，Nevada，1986.

[3]費愛國，張陸游，丁前軍.基于拍賣算法的多機協同火力分配[J].系統工程與電子技術，2012，34（9）：1828-1833.

[4]李儼，董玉娜.基于SA-DPSO混合優化算法的系統空戰火力分配[J].航空學報，2010，31（3）：626-631.

[5]陳華東，王樹宗，王航宇.基于混合粒子群算法的多平臺多武器火力分配研究[J].系統工程與電子技術，2008，30（5）：880-883.

[6]高尚，楊靜宇.武器-目標分配問題的粒子群優化算法[J].系統工程與電子技術，2005，27（7）：1250-1253.

[7]羅德林，段海濱，吳順詳.基于啟發式蟻群算法的協同多目標空戰決策研究[J].航空學報，2006，27（6）：1166-1170.

[8]Gao S.Solving weapon-target assignment problem by a new ant colony algorithm[C]//Proceedings of the 6 World Congress on Intelligent Control and Automation，2008，1：221-224.

[9]楊山亮，黃健，劉洋，等.基于遺傳算法的聯合火力WTA問題研究[J].計算機仿真，2012，29（3）：61-64.

[10]羅雪暉，楊燁，李霞.改進混合蛙跳算法求解旅行商問題[J].通信學報，2009，30（7）：130-135.

[11]裴蘭珍，甘傳付，邢波，等.采用改進差分進化算法的防空導彈火力分配[J].計算機工程與應用，2012，48（22）：235-238.

[12]Eusuff M M，Lansey K E.optimization of water distribution network design using the shuffled frog leaping algorithm[J].J of Water Resources Planning and Management，2003，129（3）：210-225.

[13]張敬敏，馬麗，李媛媛.求解TSP問題的改進混合蛙跳算法[J].計算機工程與應用，2012，48（11）：47-50.

[14]王亞敏，潘全科，冀俊忠.求解考試時間安排的離散蛙跳算法[J].計算機工程與應用，2009，45（36）：40-44.

[15]崔文華，劉曉冰，王偉，等.混合蛙跳算法研究綜述[J].控制與決策，2012，27（4）：481-487.

ZHANG Kai, ZHOU Deyun, PAN Qian

School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710129, China

In view of beyond-visual-range cooperative air combat, the model of Weapon-Target Assignment（WTA）is established,and a mixed Shuffled Frog Leaping Algorithm（SFLA）is proposed to solve the weapon-target assignment problem.Based on an unconstrained encoding, the algorithm combining the cross and mutation of genetic algorithm improves the convergence rate and the seeking ability for the global optimal result so that the local minimum is avoided. The simulation results show that the proposed algorithm is an effective algorithm to solve weapon-target assignment for cooperative air combat.

cooperative air combat; weapon-target assignment; shuffled frog leaping algorithm; genetic operator

ZHANG Kai, ZHOU Deyun, PAN Qian. Weapon-target assignment based on shuffled frog leaping algorithm in cooperative air combat. Computer Engineering and Applications, 2014, 50（17）：263-266.

A

V 247

10.3778/j.issn.1002-8331.1306-0116

航空科學基金（No.20115553021）。

張凱（1988—），男，碩士研究生，研究領域為大系統理論及應用、先進控制理論；周德云（1964—），男，教授，博士生導師；潘潛（1989—），男，碩士研究生。E-mail：zhangkainw pu@mail.nw pu.edu.cn

2013-06-13

2013-10-21

1002-8331（2014）17-0263-04

CNKI網絡優先出版：2013-11-27,http://www.cnki.net/kcm s/detail/11.2127.TP.20131127.1511.005.htm l