基于ADAMS平臺的鏈傳動建模方法及仿真研究

李增雙

（湖南華菱鋼鐵股份有限公司，湖南 湘潭 411101）

0 引 言

與帶傳動、齒輪傳動相比，鏈傳動具有傳動比準確且傳動效率高等特點［1］,因為其本身存在多邊形效應，造成較大的動載荷，所以在嚙合瞬間會對鏈節較大沖擊，引發鏈條橫向振動，造成磨損和跳齒等。鑒于鏈傳動本身的動力學特性，研究鏈傳動中鏈條的橫向振動，對于解決鏈傳動的穩定性、失效等問題有重要意義。本文通過虛擬樣機技術［2］，建立鏈傳動的多剛體多力學模型，模擬鏈傳動過程中工作環境及受力特點，提出了鏈節與鏈節之間柔性鉸約束模型和鏈節與鏈輪之間接觸模型，運用ADAMS命令流建立了鏈傳動虛擬樣機模型，并驗證了建模的準確性，對鏈傳動的振動和沖擊等問題起到很好預測作用。

1 鏈傳動的設計與計算

本文依據設計需求，采用傳動比i=1，雙鏈輪的傳動方式，選擇型號為選用08B 鏈節。它是由內鏈板、外鏈板、銷軸、套筒和滾子組成［3］，如圖1（a）所示。鏈輪中分度圓d、齒頂圓da、齒根圓df、齒側凸緣直徑dg等依據《機械設計手冊》相關公式可算出，取中心距a=533 mm，如圖1（b）所示。

2 鏈傳動多體動力學建模

針對ADAMS 對大變形柔性體建模的復雜性，本文采用命令流的方式完成鏈傳動系統的裝配、柔性鉸約束的添加，鏈節與鏈輪接觸約束的添加等操作，具有快速、準確等特點。

2.1 鏈節與鏈節之間建模

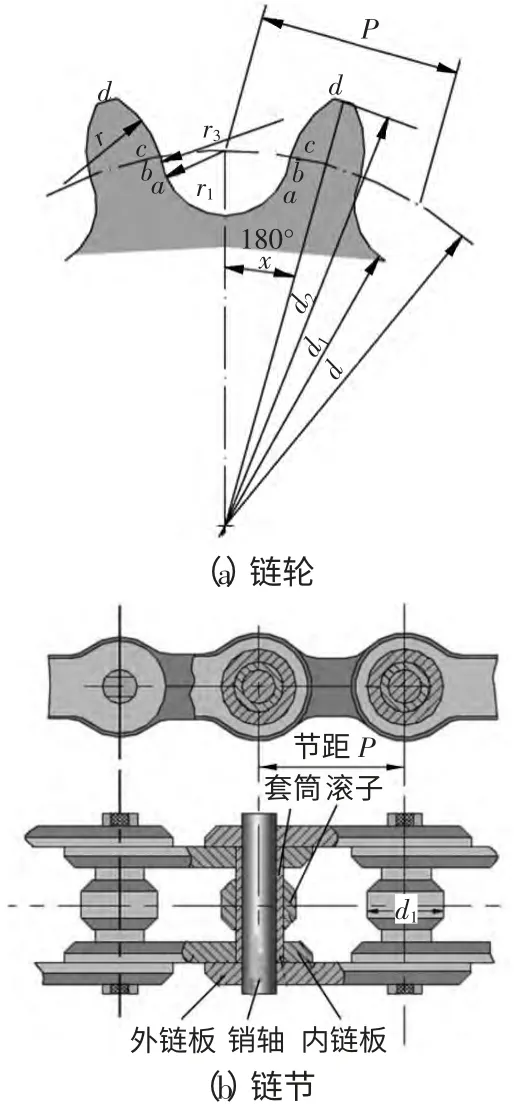
圖1 鏈輪與鏈節設計參數圖

鑒于目前鏈傳動的動力學模型有以下4 種［4］：勻質彈性帶模型、集中質量彈簧模型、變質量彈性帶模型和集中質量間隙彈簧模型。勻質與變質量彈性帶模型只考慮到鏈條的連續性，忽略了鏈節之間的間隙及發生的碰撞；另外兩種屬于離散多剛體模型，但忽略了鉸接處的微小位移。考慮到兩個鏈節之間具有相互轉動、橫向位移以及縱向線位移的特性，本文提出了采用軸套約束來模擬兩鏈節之間的約束。軸套力通過定義力和力矩的6 個分量（FXFYFZTXTYTZ）在兩個構件之間添加一種相互作用力［5］，如圖2 所示。軸套力計算公式如下所示：

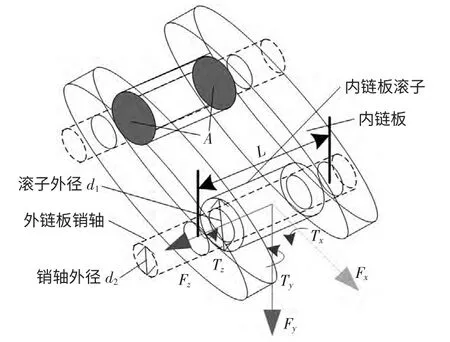
圖2 鏈節受力示意圖

式中：K 為剛度；C 為阻尼；X、Y、Z、a、b、c 為變形量；vX、vY、vZ、ωX、ωY、ωZ為分量速度；F1、F2、F3、T1、T2、T3為預載荷。

式（2）中：K 為碰撞剛度；g 為切入深度；dmax為最大切入深度；e 為力指數；cmax為最大滲入深度時達到的最大阻尼；dg/dt 為滲入速度。

2.2 鏈節與鏈輪之間建模

在ADAMS 中接觸可分為連續接觸和瞬時接觸。計算接觸力有沖擊函數模型和泊松模型。沖擊函數模型表達式為。 （3）

式中：p 為罰參數；ε 為恢復系數。

參數選擇較大收斂變慢，選擇較小則很難保證其單向約束條件。采用改進拉格朗日模型，采用迭代方法求解接觸力，其公式為

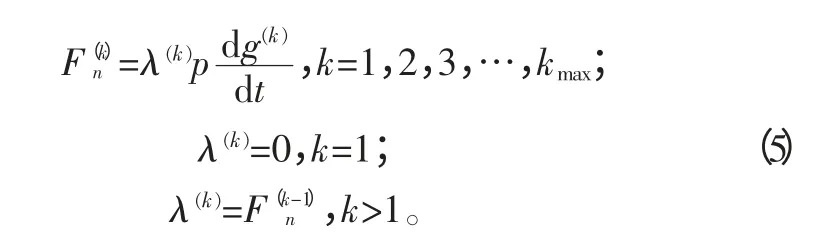
式中，k 為迭代步數。

通過上述過程，完成了對鏈傳動系統虛擬樣機的建模，共包括128 個剛體，4 個轉動副、124 個軸套約束、124個接觸約束，如圖3 所示。

圖3 鏈傳動系統虛擬樣機

3 鏈傳動的仿真驗證及結果分析

3.1 仿真驗證

鏈傳動按鏈節所處的位置可分為以下4 個部分：主動輪驅動部分、從動輪部分、緊邊部分和松邊部分，如圖4所示。本文采用驗證鏈傳動的緊邊力與松邊力的方法，即通過仿真測出緊邊力與松邊力，然后同理論計算值相比較，計算誤差是否在符合范圍內來確定鏈傳動的建模是否準確。

依據《機械設計》，鏈傳動緊邊拉力

鏈傳動松邊所受到拉力

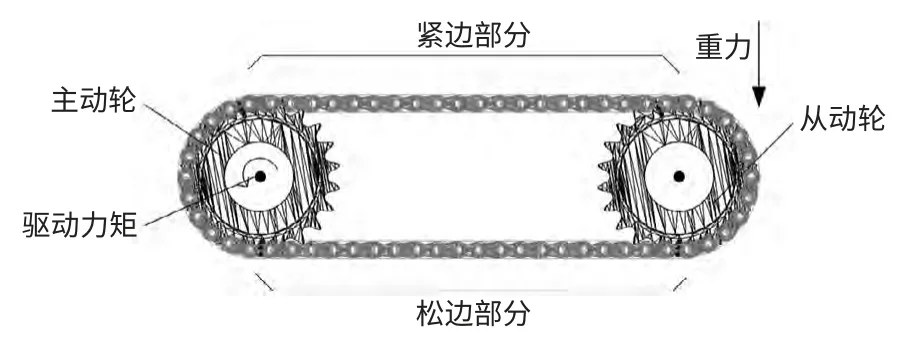
圖4 鏈傳動機構

式中：Fe為有效圓周力，Fe=1 000P/ν；Fc為離心力引起的拉力，Fc=qv2；Ff為懸垂拉力，Ff=Kfqa×10-2。

本文中依據所選鏈節型號，垂度系數Kf=1.5，鏈節速度v=0.09 m/s，q=0.7 kg/m。

依據上述參數帶入公式中得：F1＝178.27 N，F2＝161.57 N，為保證所得曲線能夠最大限度地反映真實情況，設定仿真時間為5 s，緊邊力與松邊力仿真結果如圖5、圖6 所示

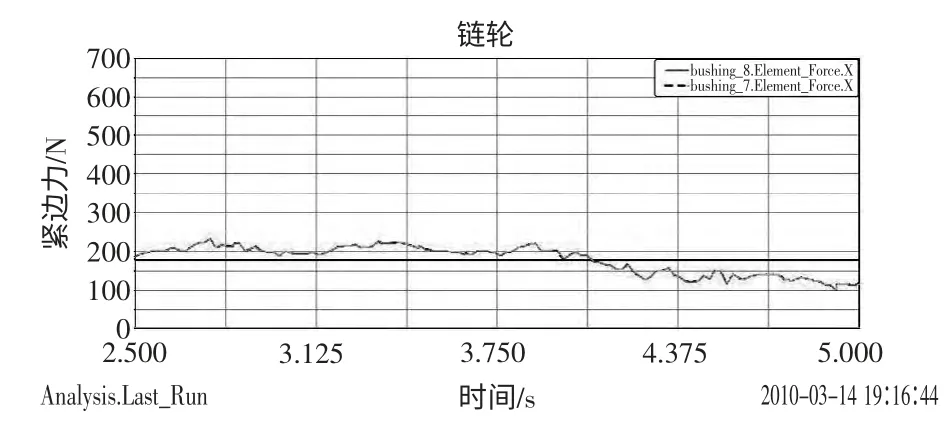
圖5 緊邊力變化圖

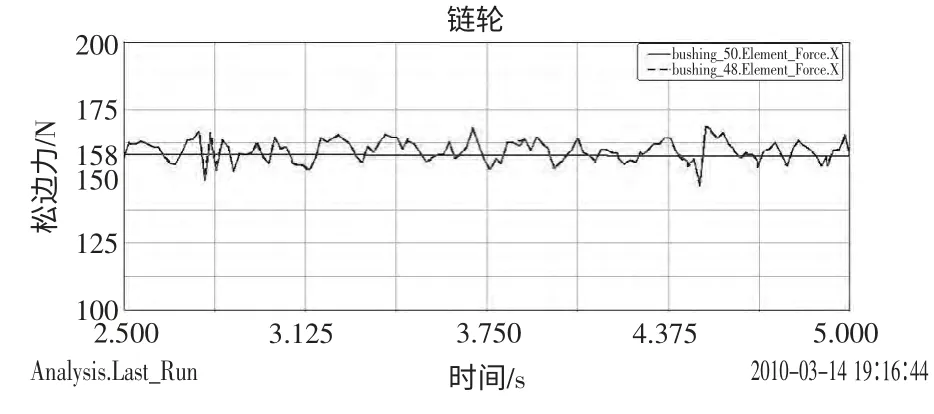
圖6 松邊力變化圖

對緊邊力和松邊力的仿真曲線積分，然后對時間做除法運算，得到力的平均值。緊邊力平均值為F1=177.29 N，與理論值的誤差為η=0.5%；松邊力平均值F2=158.4 N，與理論值的誤差為η=2.0%。考慮到鏈輪與鏈節之間摩擦、軸承之間摩擦等因素的影響，閉式鏈的誤差范圍為0～5%，計算結果在此范圍內，從而驗證了鏈傳動動力學建模的正確性。

3.2 結果分析

針對鏈傳動中的多邊形效應對鏈節的沖擊，本文主要研究鏈節橫向、縱向的速度、加速度變化以及鏈節與鏈輪之間接觸力的變化，來反映鏈傳動的運動特性。

由圖7、圖8 可知，鏈節在往復運動過程中，受到的橫向沖擊明顯要大于受到的縱向沖擊；在階躍點處，加速度變化較大；鏈節在運動過程中，進出嚙合點的加速度變化明顯，沖擊較大。

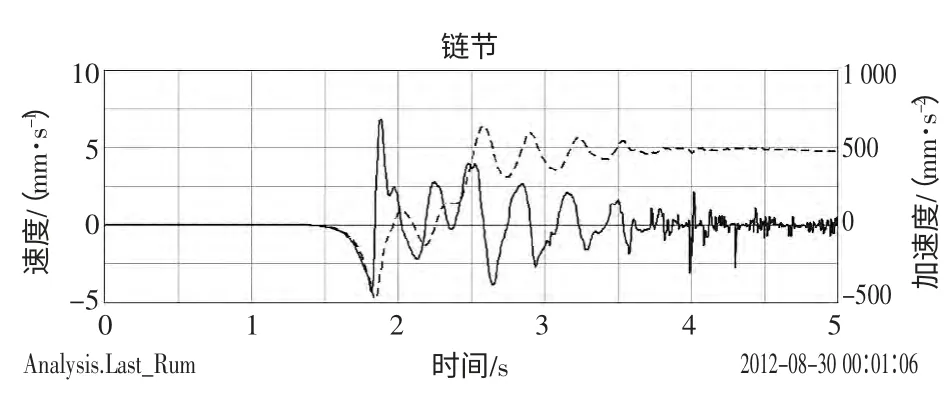
圖7 鏈節橫向速度、加速度變化圖

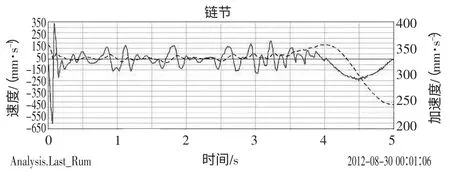
圖8 鏈節縱向速度、加速度變化圖

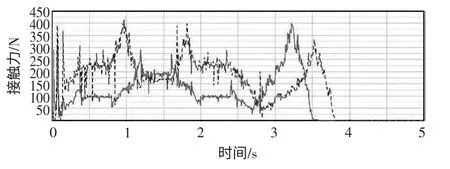
圖9 鏈節與主動、從動鏈輪接觸力變化圖

圖9 為鏈節14 與主動輪的接觸力曲線以及鏈節32與從動輪的接觸力曲線變化圖，可知鏈節越靠近緊邊接觸力值愈大，越靠近松邊接觸力值愈小，從鏈節嚙入到嚙出過程中，鏈節愈靠近緊邊接觸力變化愈快，接觸力出現峰值的點較少，變化較平穩。

4 結 論

本文提出用軸套力約束來模擬鏈節之間受力的多剛體動力學模型，運用ADAMS 命令流建立了鏈傳動系統的多體動力學仿真模型，并進行仿真，仿真結果驗證了鏈傳動建模的正確性，對鏈節振動以及鏈輪之間的沖擊問題進行很好的預測。

［1］ JohnsonKL.ContactMechanics［M］.London：Cambridge University Press，1985：15-28.

［2］ 芮執元，魏興春，馮瑞成.基于ADAMS 的虛擬樣機技術及其在機構設計中的應用［J］.科學技術與工程，2006（19）：3111-3114.

［3］ 濮良貴，紀名剛.機械設計［M］.7 版.北京：高等教育出版社，2001.

［4］ 蒲明輝，吳江.基于ADAMS 的鏈傳動多體動力學模型研究［J］.機械設計與研究，2008（24）：2-3.

［5］ Kim H N．Impact dynamics of axially moving chains with tensioner［D］.Pennsylvania State University，1997：1-3，80-82.