撈油抽子密封橡膠筒力學性能研究

崔健，謝勁松

（長春理工大學 機電工程學院，長春 130022）

0 引 言

隨著石油資源的消耗，地下油層的含油量也在逐漸降低，這導致部分油井產油率下降，傳統的抽油方式已不適合在此類產油低的井上工作。因此，在最近十年中一種新型采油方式得到發展，柔性撈油抽子替代了剛性抽油桿和泵的組合方式，與傳統抽油方式相比，它克服了小沖程、多沖次的缺點，可以實現長沖程，同時降低了沖程次數。其中密封橡膠筒這一零件至關重要，通過撈油抽子在井下的往復運動，液柱自身重力使密封橡膠筒膨脹或復原，以實現提撈油的功能。但是在這一工作過程中存在一個矛盾問題，密封橡膠筒在與管壁接觸時必定會與管壁產生摩擦，因為密封橡膠筒變形過大會導致磨損程度發生變化，過度磨損會加劇抽子損壞，直接加大了抽油漏失率。因此，需要找到在密封橡膠筒形變、應力、與摩擦力、磨損之間的關系。

1 密封橡膠筒幾何模型建立

依據撈油抽子工作原理和加工工藝要求建立密封橡膠筒模型，如圖1 所示。

圖1 密封橡膠筒

2 密封橡膠筒形變、應力、摩擦力、磨損之間關系建模

密封橡膠筒的形變、應力與材料力學、彈性力學相關，摩擦力隨著井下位置變動而變化，在其它因素不變的情況下，磨損與摩擦力成線性關系。

2.1 理論模型基本假定

1）假定橡膠密封筒工作范圍在彈性變形范圍內，并且不會達到塑性變形。2）在滿足工作要求下對密封橡膠筒實物進行簡化處理，例如去掉倒角、螺紋等。3）剛性油管相對于彈性密封橡膠筒接觸過程中產生的形變忽略不計。4）假定橡膠密封筒是均勻的、具有各向同性［1］。5）密封橡膠筒軸向、徑向上受均布載荷。

2.2 數學模型的建立

如圖2 所示，由于密封橡膠筒是回轉體，在井下其受力狀況相對于軸線對稱，且軸向受力和徑向受力情況都為均布載荷，所以對于軸對稱受力問題設在極坐標下考慮［2］。

另外，由于密封橡膠筒變形后與油管內壁完全接觸，在井下特定位置下它將不變形，軸向上不會產生伸縮，但同時受到液柱重力影響，內部會產生軸向應力。因此將其簡化為平面應變問題。即橡膠筒內半徑為a，與油管內壁接觸時外半徑為b，受內壓qa，油管內壁給的外壓qb。

1）推導所需主要符號：直角坐標x，y，z；極坐標ρ，φ；體力分量fp，fφ（極坐標系）；應力分量正應力σ，切應力τ；應變分量線應變ε，切應變γ；應力函數Φ，密度ρ液，重力加速度g 橡膠筒距離井口位移h；彈性模量E，切變模量G，泊松比μ，動摩擦因數f；幾何尺寸橡膠筒內半徑a，橡膠筒與油管內壁的外半徑b，接觸厚度c。量綱采用國際單位制（SI）。

2）依據上述假設，由彈性力學公式得極坐標中的平衡微分方程［2-3］：

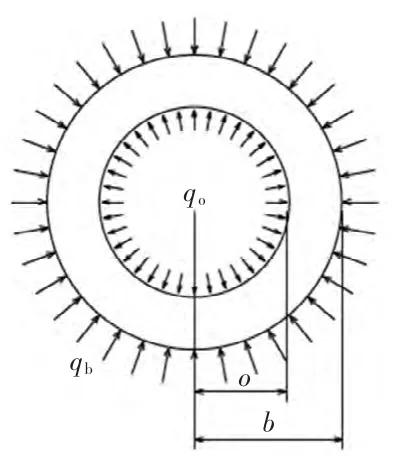
圖2 橡膠筒受力分布

根據實際情況密封橡膠筒的徑向、周向不受外力，故fρ=0，fφ＝0。

3）由彈性力學知，極坐標中的幾何方程

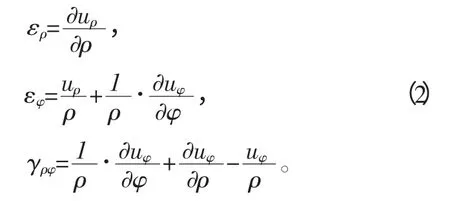
4）由彈性力學得極坐標中的平面應變物理方程：

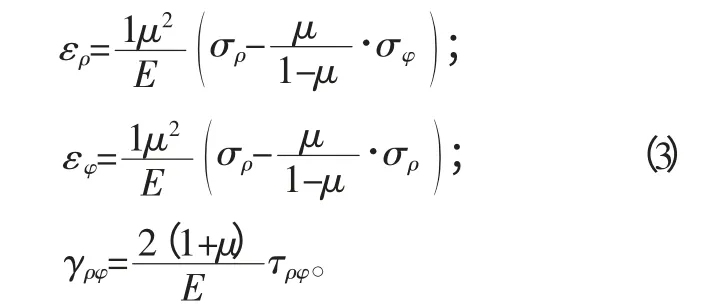
5）由彈性力學得，應力函數Φ 可以表達極坐標中的應力分量如下式。

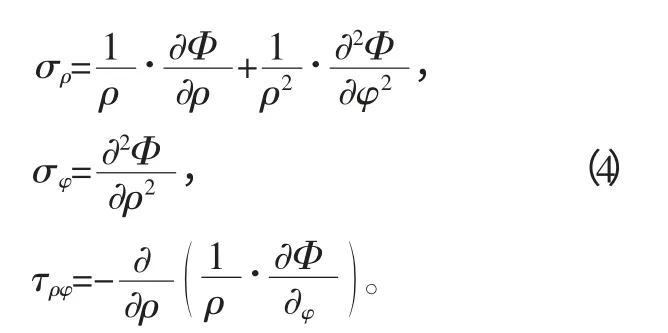
6）極坐標中的相容方程

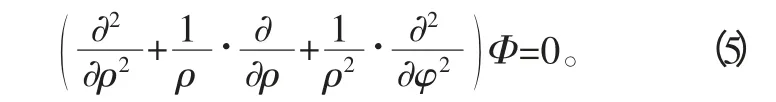
由于密封橡膠筒是軸對稱應力，所以用彈性力學中逆解法求解應力函數，應力函數Φ 只是徑向坐標ρ 的函數，即：Φ＝Φ（ρ）。

在這樣情況下，式（4）簡化為：

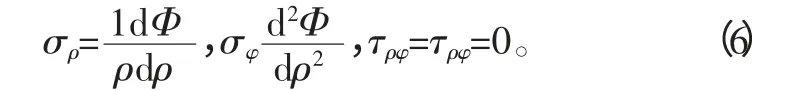
將式（6）帶入到（5）得出：

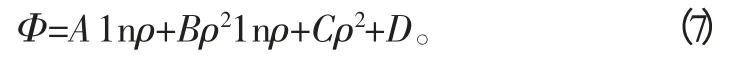
（7）式中A、B、C、D 為任意常數。將式（7）帶入到式（6）中得應力分量：

由式（8）知，求出任意常數A、B、C 則應力分量表達式確定。

7）根據邊界條件要求：

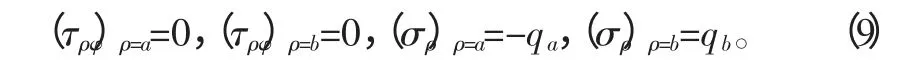
帶入式（8）整理后得拉梅方程

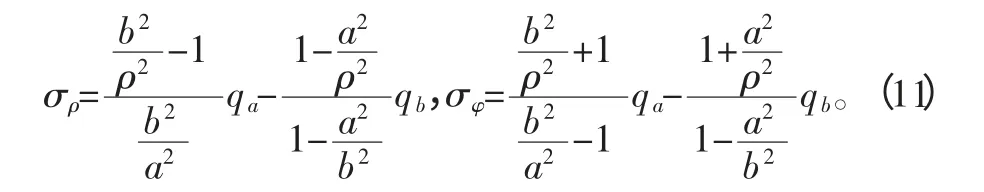
8）由彈性力學應力坐標變換公式：

得出公式： σxσy=σρσφ（12）

得 σz＝μ（σx+σy）。 （13）

將式（11）帶入式（13）中得：

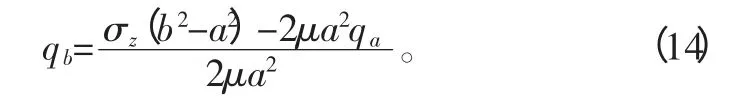
由于密封橡膠筒端部受均布載荷（液柱重力作用橡膠筒端面），其端面主矢不等于0、主矩等于0 符合靜力等效原則，根據圣維南原理得出邊界條件：

根據物理學知識，物體在同一位置上受到液體產生的壓強大小相等，再根據基本假定5 得：

將式（15）和（16）帶入到式（14）中整理得：

2.3 物理模型建立

根據動摩擦力［4］公式F=f·FN。 （18）

密封橡膠筒在工作過程中，油管壁與筒壁產生相互的作用力，又因為彈性力學知邊界條件下應力與面力大小相等。因此 EN＝qb·S，S=π·b·c。 （19）

最后將式（19）與（17）帶入式（18）中，整理得：

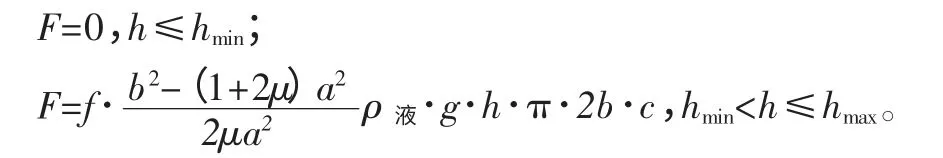
即：F=0，0＜h≤hmin；F=K·h，hmin＜h≤hmax。 （20）其中系數K 作為幾何參數a 和泊松比μ 之間的函數。hmin由材料力學限定，hmax由塑性力學限定。

3 試驗結果分析

試驗結果與理論計算結果存在誤差，出現誤差的原因是隨機因素引起。但誤差在可控范圍內，符合工程實際需求。試驗結果如表1、圖3、圖4 所示。

4 結 語

推導出的結論分如下幾部分表述，1）幾何參數包括a、b、c，根據工程需要a 可以為變量，其它為常量；2）材料特性，橡膠筒泊松比μ 可以通過改變材料配方來改變其值，可以認為是變量。因此對于密封橡膠筒對油管內壁摩擦力問題通過幾何尺寸、材料性質對其進行定量分析。

表1 參數表

圖3 摩擦力與井下位移關系

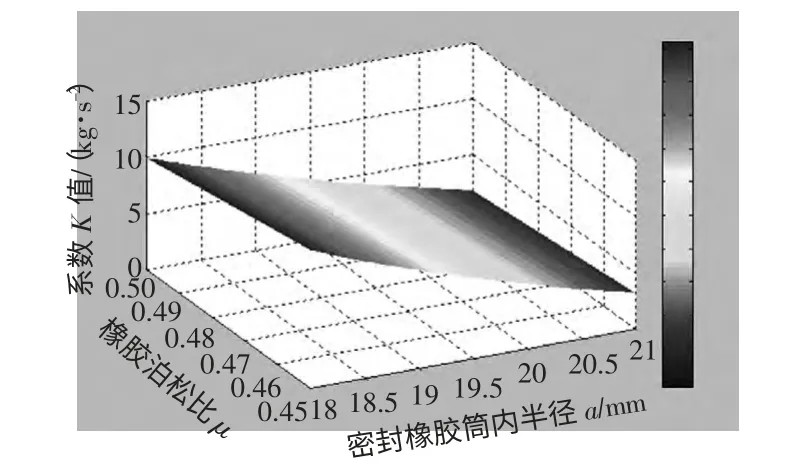
圖4 系數K 與橡膠筒內半徑、泊松比關系

［1］ S.P.鐵木辛柯，J.N.古地爾.彈性理論［M］.北京：高等教育出版社，2013：75-88.

［2］ 徐芝綸.彈性力學［M］.北京：高等教育出版社，2006.

［3］ 谷超豪，李大潛，陳怒行.數學物理方程［M］.2 版.北京：高等教育出版社，2002：68-91.

［4］ 哈爾濱工業大學理論力學教研室.理論力學［M］.北京：高等教育出版社，2009：112-114.