兩級定位-路徑問題的變鄰域人工蜂群算法

陳久梅，龔英

1.重慶工商大學電子商務及供應鏈系統重慶市重點實驗室，重慶 400067

2.重慶工商大學商務策劃學院，重慶 400067

兩級定位-路徑問題的變鄰域人工蜂群算法

陳久梅1，2，龔英1，2

1.重慶工商大學電子商務及供應鏈系統重慶市重點實驗室，重慶 400067

2.重慶工商大學商務策劃學院，重慶 400067

建立了兩級定位-路徑問題的數學模型，提出了一種求解該問題的人工蜂群算法。針對該算法容易出現早熟現象，將近年來國外出現的一種新穎的軌跡式啟發式算法——變鄰域搜索融入其中，由此提出三種變鄰域搜索策略。基于不同變鄰域搜索策略的人工蜂群算法和人工魚群算法的求解效果進行對比仿真。實驗結果表明，變鄰域人工蜂群算法能有效求解兩級定位-路徑問題。

兩級定位-路徑問題；人工蜂群算法；變鄰域搜索；物流；配送

1 引言

近年來，物流進城難、成本高、送錯貨等問題屢見不鮮。為了解決這些問題，提高配送能力，越來越多的企業在城市周邊設立中轉站，用于進城物品的分揀、拼裝和轉運。由此形成由“配送中心-中轉站-顧客”為節點的兩級物流網絡。該網絡中涉及到的配送中心、中轉站的位置、數量，兩級網絡各節點間的任務分配，以及車輛的調度與配送路徑等問題的集成，即兩級定位-路徑問題（two-Echelon Location-Routing Problem，2E-LRP）[1]。該問題自Jacobsen等[2]提出以來，逐漸成為研究熱點。

兩級定位-路徑問題是一個NP-Hard問題，目前的研究主要集中在啟發式求解算法方面。Ambrosino等[3]用大規模鄰域搜索算法和重新定位機制求解只有一個配送中心的帶異質車隊的兩級定位-路徑問題。Sterle等[4]為設施點有容量限制的兩級定位-路徑問題建立整數規劃模型，使用禁忌搜索算法進行求解。Jin等[5]使用遺傳算法和禁忌搜索算法的混合算法求解兩級定位-路徑問題。Boccia等[6]首先將兩級定位-路徑問題分解為兩個一級定位-路徑問題，每個一級定位-路徑問題進一步分解為設施定位問題和車輛路徑問題，之后使用多階段迭代嵌入禁忌搜索算法進行求解。王紹仁等[7]針對震后緊急響應階段應急物流系統優化中的兩級定位-路徑問題，提出了一種基于兩階段分段思想的“三角”啟發式算法進行求解。Nguyen等[8-9]采用貪婪隨機自適應搜索、路徑重連及學習過程求解兩級定位-路徑問題。

人工蜂群算法（Artificial Bee Colony，ABC）是由Karaboga[10]于2005年基于蜜蜂覓食原理提出的一種群智能優化算法。它模擬了蜂群依各自分工不同協作采蜜，交換蜜源信息尋找最優蜜源的群體行為。它已被廣泛應用于求解旅行商問題、車輛路徑問題及設施定位等NP-Hard問題，均取得較好的求解效果。該算法具有良好的求取全局極值能力，并具有對初值、參數選擇不敏感、魯棒性強、簡單易實現等優點，但卻存在搜索早期過早收斂、搜索后期收斂較慢等問題[10]。近年來，國外出現了一種新穎的軌跡式啟發式算法——變鄰域搜索（Variable Neighborhood Search，VNS）。該算法的基本思想是在獲得局部最優解的基礎上，通過系統地改變鄰域結構集來拓展搜索范圍找到另一個局部最優解。該算法思想簡單，容易實現，算法結構與問題無關，適合于各類優化問題，它可被方便地嵌入到其他啟發式算法中[11]。在此，針對人工蜂群算法存在的不足，設計嵌入變鄰域搜索的人工蜂群算法對兩級定位-路徑問題進行求解。

2 問題描述及數學建模

2.1 問題描述

兩級定位-路徑問題是傳統定位-路徑問題的拓展問題，是兩級物流網絡中的定位-路徑問題，其中涉及到配送中心和中轉站兩類物流設施的選址、設施與需求點之間的配給以及兩級物流網絡中車輛的行駛路徑。具體可描述如下：由一系列潛在配送中心、潛在中轉站及已知顧客所構成的兩級物流網絡中，物品從配送中心經中轉站到達顧客處，在滿足設施容量限制、車輛容量限制等約束條件下，確定哪些潛在設施點開放、開放的配送中心應分別為哪些開放的中轉站提供物品、開放的中轉站應分別為哪些顧客提供物品、兩級物流網絡中各需多少輛車及每輛車的行駛路線，以實現總成本最小，即兩級設施點的開放成本、車輛的使用成本及車輛的運行成本之和最小。該問題的假設條件如下：

（1）兩級物流網絡中所使用的車輛、兩級設施均有容量限制。

（2）每個顧客只能接受來自一個已開放中轉站的物品，每個開放的中轉站只能接受來自一個已開放配送中心的物品。

（3）二級物流網絡中每個顧客只能接受一輛車、一次服務，一級物流網絡中每個開放的中轉站只能接受一輛車、一次服務。

（4）物品從配送中心出發，必須經過中轉站中轉才能到達顧客處，不考慮配送中心直接送達顧客的情況，且同級設施之間無貨物流動。

（5）物流網絡中每輛車僅完成一次旅行，且二級物流網絡中車輛從某中轉站出發完成行駛路徑上所有顧客需求服務后必須回到該中轉站，一級物流網絡中車輛從某配送中心出發完成行駛路徑上所有中轉站需求服務后必須回到該配送中心。

（6）車輛行駛成本行駛距離成正比。

2.2 數學建模

2.2.1 符號說明

集合：ND為潛在配送中心集合；NS為潛在中轉站集合；NC為顧客集合；E1為一級物流網絡邊的集合；E2為二級物流網絡邊的集合；P，R，T?ND∪NS∪NC，Z?E1∪E2。

參數：QDi為配送中心i的容量；FDi為配送中心i的開放成本；QSi為中轉站i的容量；FSi為中轉站i的開放成本；QVi為i級物流網絡中車輛的容量(i=1，2)；FVi為i級物流網絡中車輛的固定使用成本(i=1，2)；cij為邊(i，j)上車輛行駛成本；di為顧客i的需求量。

決策變量：uij為一級物流網絡中邊(i，j)被使用一次為1，否則為0；vij為一級物流網絡中邊(i，j)被使用兩次為1，否則為0；xij為二級物流網絡中邊(i，j)被使用一次為1，否則為0；yij為二級物流網絡中邊(i，j)被使用兩次為1，否則為0；mij為中轉站i分配給顧客j為1，否則為0；nij為配送中心i分配給中轉站j為1，否則為0；oi為配送中心i開放為1，否則為0；pi為中轉站i開放為1，否則為0。

2.2.2 模型建立

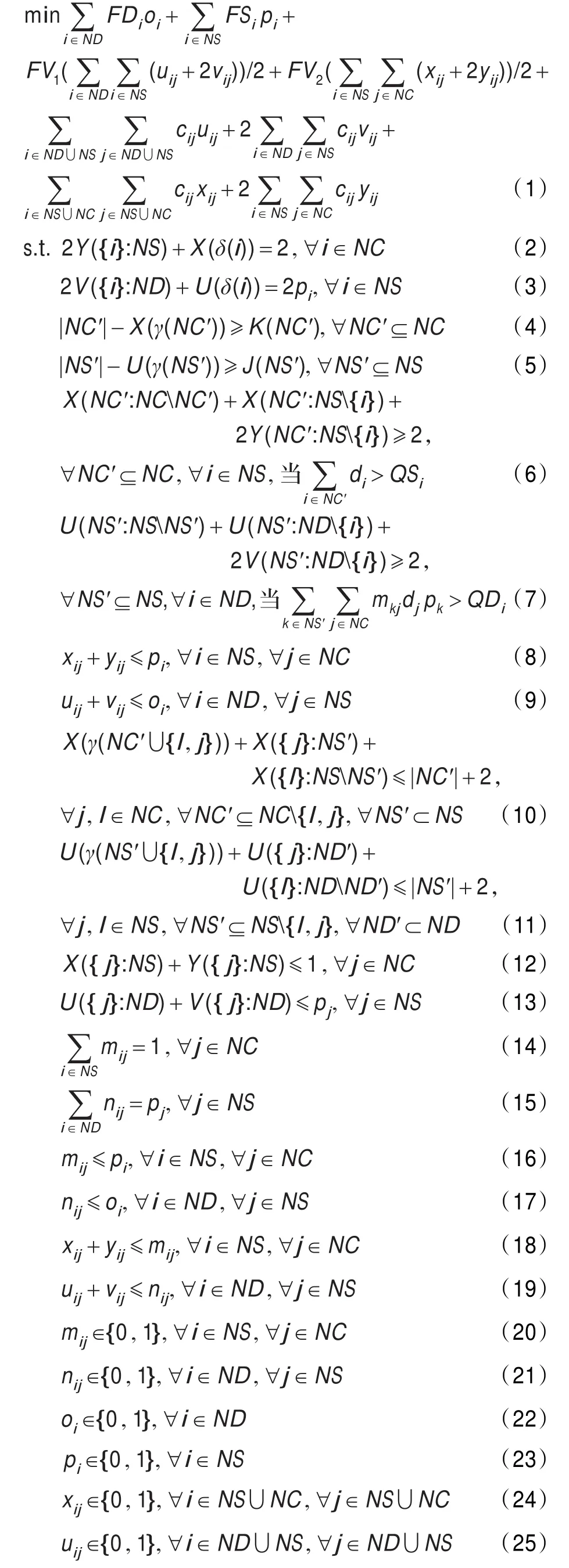
上述模型中，目標函數由八部分組成，其中，第一、二項分別為配送中心和中轉站的開放成本，第三、四項分別為一、二級網絡中車輛固定使用成本。第五、六項為一級網絡中車輛行駛成本，第七、八項為二級網絡中車輛行駛成本。

式（2）～（27）為該問題的約束條件，式（2）表示二級物流網絡中對任意一個顧客，連接該顧客的邊有兩條；式（3）表示一級物流網絡中如果某中轉站開放，那么連接該中轉站的邊有兩條，否則沒有邊連接該中轉站；式（4）表示二級物流網絡中車輛運輸量不能超過車輛的容量，當K(NC′)=1時，表示子回路消除；式（5）表示一級物流網絡中車輛運輸量不能超過車輛的容量，當K(NS′)=1時，表示子回路消除；式（6）表示分配給某中轉站的顧客需求量之和不超過該中轉站的容量；式（7）表示分配給某配送中心的中轉站貨物量之和不超過該配送中心的容量；式（8）表示二級物流網絡中，如果某中轉站開放，那么連接該中轉站與某顧客的被使用一次和兩次的邊不能同時存在，否則沒有邊連接該中轉站；式（9）表示一級物流網絡中，如果某配送中心開放，那么連接該配送中心與某中轉站的用一次和兩次的邊不能同時存在，否則沒有邊連接該配送中心；式（10）表示顧客數不小于2的二級物流網絡中，從某中轉站出發的車輛，完成配送后必須回到該中轉站；式（11）表示中轉站數不小于2的一級物流網絡中，從某配送中心出發的車輛，完成配送后必須回到該配送中心；式（12）表示二級物流網絡中對任意顧客，連接該顧客與中轉站的被使用一次和兩次的邊的數量之和小于等于1；式（13）表示一級物流網絡中，如果中轉站開放，連接該中轉站與配送中心的被使用一次和兩次的邊的數量之和小于等于1，如果中轉站不開放，沒有邊連接；式（14）表示對任意一個顧客，有且僅有一個中轉站配給；式（15）表示對任意一個中轉站，若開放則有且僅有一個配送中心配給，否則無配送中心配給；式（16）表示如果某中轉站分配給某顧客，則該中轉站一定開放，如果某中轉站未開放，則一定不能分配給任何顧客；式（17）表示如果某配送中心分配給某中轉站，則該配送中心一定開放，如果某配送中心未開放，則一定不能分配給任何中轉站；式（18）表示若某顧客沒有分配給某中轉站，則兩者之間的邊不能被訪問，若某顧客分配給某中轉站，則連接兩者的被使用一次和使用兩次的邊不能同時存在；式（19）表示若某中轉站沒有分配給某配送中心，則該兩者之間的邊不能被訪問，若某中轉站分配給某配送中心，則連接兩者的被使用一次和使用兩次的邊不能同時存在；式（20）～（27）為決策變量的取值范圍。

3 算法設計

人工蜂群算法模擬蜂群的采蜜行為，通過不同角色蜜蜂間的信息交流、角色轉換和分工協作來找到問題的最優解。人工蜂群由引領蜂、跟隨蜂和偵察蜂組成。引領蜂在蜜源處采蜜并提供所記憶的蜜源信息；跟隨蜂以一定的概率選擇某個引領蜂去蜜源處采蜜；偵察蜂負責尋找新蜜源。其中蜜源的位置代表優化問題的可行解，蜜源的花蜜含量代表解的質量，稱為適應值。

ABC算法工作原理如下：引領蜂尋找蜜源，跟隨蜂選擇并跟隨引領蜂在相應的蜜源位置附近進行鄰域搜索，若能搜索到適應值更高的新蜜源，則更新當前蜜源。如果某個蜜源的位置不能在預先設定的循環次數內得到進一步改進，則放棄該蜜源，將其對應的引領蜂轉換為偵察蜂。被放棄的蜜源將由偵察蜂找到的新蜜源所取代，此時偵察蜂轉換為與新蜜源對應的引領蜂。跟隨蜂再次選擇引領蜂跟隨。如此反復迭代，直到達到結束條件為止。

3.1 算法總體框架

針對兩級定位-路徑問題，本文在引領蜂及跟隨蜂所進行的鄰域搜索過程中嵌入變鄰域搜索算法，即在鄰域搜索過程中系統地改變鄰域結構集來拓展搜索范圍。具體步驟如下：

步驟1初始化種群參數SN，limit，此時所有蜜蜂為偵察蜂。

步驟2生成SN個初始解，按目標函數值從小到大排序，前一半的解設為當前解，此時一半偵察蜂轉換為引領蜂并各自攜帶一個當前解，一半偵察蜂轉換為跟隨蜂。

步驟3計算每個引領蜂攜帶解被選擇的概率Pi，引領蜂根據Pi招募跟隨蜂。

步驟4每一只引領蜂及其跟隨蜂對其攜帶的當前解進行變鄰域搜索，若搜索到比當前解更優的解，則替換當前解；否則，繼續進行變鄰域搜索，直到達到一定次數limit，若此時仍然未搜索到更優解，則該引領蜂轉換為偵察蜂。

步驟5偵察蜂進行全局搜索得到新解，并用新解替換當前解，此時偵察蜂變為引領蜂。

步驟6當所有引領蜂對其攜帶當前解進行變鄰域搜索后，將種群最優解進行保存；若滿足程序終止條件，則程序退出，輸出種群最優解，否則轉步驟3。

3.2 初始解的生成

在此將兩級定位-路徑問題分為兩級，每級進一步劃分為設施定位和車輛路徑兩個子問題。設施定位問題采用隨機最近鄰策略求解，車輛路徑問題采用經典的C-W節約算法進行求解。具體來說，在由中轉站與顧客構成的二級網絡中，首先隨機選擇未開放的中轉站并將其開放；之后，從距離最近的r個未歸給任何中轉站的顧客中隨機選擇某個顧客，并將其歸給該中轉站，重復此步，直到所有顧客均已歸入某中轉站或超過該中轉站容量限制為止；若存在未歸入任意中轉站的顧客，則隨機選擇未開放的中轉站并將其開放；按上述方法將相應顧客逐一歸入；重復此步，直到所有顧客均歸入某相應中轉站為止，從而完成二級網絡中設施定位問題的求解。按類似的方法，完成由配送中心與中轉站構成的一級網絡中設施點定位問題的求解。最后，分別針對開放的配送中心、中轉站，根據車輛容量限制，使用C-W算法求解兩級網絡中的車輛路徑問題。

3.3 鄰域解的產生

兩級定位-路徑問題，其產生鄰域解的考慮對象有兩級物流網絡中的顧客、中轉站及路徑三類。以顧客為對象的鄰域解采用單個顧客位置的移動（記為N1）及兩個顧客之間位置的交換（記為N2）兩種方式來產生；以路徑為對象的鄰域解采用常用的2-opt方式（記為N3）產生；以中轉站為對象的鄰域解采用單個中轉站開放與否的狀態改變（記為N4）及兩個狀態不同的中轉站之間進行狀態交換（記為N5）兩種方式產生。

據此提出三種變鄰域搜索策略：

變鄰域搜索策略1（記為S1），順序執行各鄰域搜索，若出現比當前解更優的鄰域解，則回到N1繼續執行，一旦出現比該鄰域解更差的鄰域解，則繼續執行下一步，否則，回到N1繼續執行；否則，繼續執行下一步，直到結束。

變鄰域搜索策略2（記為S2），順序執行各鄰域搜索，若出現比當前解更優的鄰域解，則繼續用該鄰域搜索模塊進行搜索，直到比該鄰域解更差的解出現，否則，繼續執行下一步，直到結束。

變鄰域搜索策略3（記為S3），順序執行各鄰域搜索，若出現比當前解更優的鄰域解，則結束；否則，繼續執行下一步，直到結束。

3.4 選擇概率的確定

在此采用人工蜂群算法常用選擇概率計算方法，即錦標賽選擇策略。錦標賽選擇策略是基于局部競爭機制的選擇過程，即在種群中隨機選擇q個個體（競賽規模）進行比較，適應度值大的被選中，并對其加權值1；如當q=2時，將種群中個體兩兩比較，并給適應度值好的個體加權值1，對所有個體重復這一操作過程。根據個體權值，由此計算選擇概率：

其中，ai為個體i的權值。

該選擇策略中選擇概率的計算只涉及個體適應度值之間的大小關系，不涉及適應度值的具體取值，能較好避免陷入早熟。

4 算例分析

為分析變鄰域人工蜂群算法求解兩級定位-路徑問題的性能，需用算例進行仿真測試。由于該問題目前缺乏公認的國際算例，本文在文獻[12]一級定位-路徑問題算例25點、50點、75點基礎上，選擇前面部分設施點作為兩級定位-路徑問題的潛在配送中心、剩余設施點作為潛在中轉站、顧客點不變產生兩級定位-路徑問題的算例（算例中各類節點依次編號）。算例需補充和調整的參數如表1所示，其余參數詳見文獻[12]。

表1 補充、調整的參數

在此使用C sharp編程實現不同變鄰域搜索策略下的人工蜂群算法，在Windows XP系統，Pentium?Dual-Core CPU E5700@3.00 GHz、2.00 GB內存的計算環境下，對上述三組不同規模大小的算例進行求解。種群規模SN=50，算法最大迭代次數Tmax=600，鄰域搜索最大迭代次數limit=5，初始解生成過程中所用參數r=4，車輛行駛成本與其行駛距離的比例系數取1。

4.1 采用不同變鄰域搜索求解效果比較

在此分別采用不同變鄰域搜索策略的人工蜂群算法求解兩級定位-路徑問題的上述算例。隨機運行50次的求解結果見表2所示。

由表2可知，采用鄰域搜索策略S1求解時，取得的最好解和平均解較優；采用鄰域搜索策略S2求解時，取得的最差解較優；采用鄰域搜索策略S3求解時，平均計算時間較短。

以下給出分別采用S1、S2、S3三種變鄰域搜索策略的人工蜂群算法求解算例“1-4-20”，隨機運行50次種群最好解隨迭代次數變化趨勢圖，見圖1所示。

從圖1可知，采用變鄰域搜索策略S1、S2、S3求解時均能較好避免早熟，隨著迭代次數的增加，目標函數值不斷下降，算法具有較好的收斂性。

4.2 不同算法的求解效果比較

為了進一步了解變鄰域人工蜂群算法求解兩級定位-路徑問題的求解效果，在此采用人工魚群算法進行對比。借鑒文獻[13]的研究成果，將人工魚群算法的參數設置如下：最大試探次數try-number=5，擁擠度因子σ=0.4，可視范圍visual=(Ymax-Ymin)/4，其中Ymax、Ymin為當代種群最好解、最差解對應的目標函數值。人工魚群算法的運行環境與上述相同。隨機運行50次，兩種算法求解結果見表3所示。

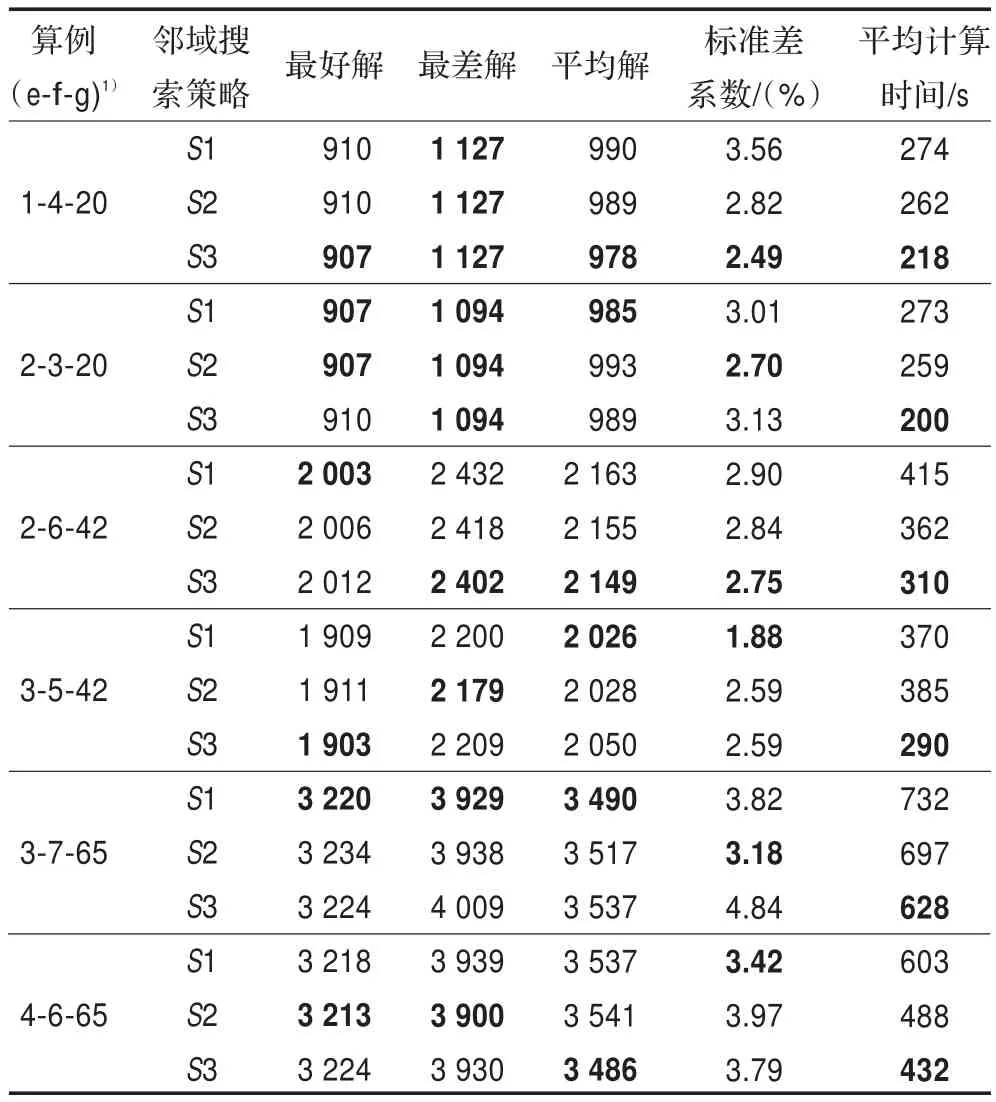
表2 不同鄰域搜索策略求解效果比較

圖1 種群最好解隨迭代次數的變化趨勢

由表3可知，人工魚群算法在最差解及平均解方面較優，變鄰域人工蜂群算法在最好解及平均計算時間方面較優。

4.3 算例最好解網絡結構

在此，給出算例“3-7-65”最好解“3 220”對應的網絡結構圖，見圖2所示。

從圖2可知，潛在的3個配送中心中開放了編號為“1”的1個配送中心，潛在的7個中轉站中開放了編號為“1”、“2”、“3”和“7”的4個中轉站，從配送中心出發到達各中轉站的路徑數為2，從各中轉站出發到達各顧客點的路徑數為12。根據該算例的相關數據，可驗證該最好解滿足假設條件（1）、（2）、（3）、（4）。由假設條件（5）可知，一級網絡車輛數即為2，二級網絡車輛數即為12。根據網絡中各節點的坐標，采用歐幾里德距離計算點與點之間的距離，求和取整得到各條路徑的長度，根據假設條件（6）可計算出各條路徑車輛行駛成本910（限于篇幅，詳細計算過程在此從略）。由此，可計算目標函數=配送中心開放成本750×1+中轉站開放成本150×4+一級網絡車輛使用成本為240×2+二級網絡車輛使用成本40×12+兩級網絡中車輛行駛成本910=3 220。進一步分析，由文獻[12]可計算出該算例的顧客需求量為1 168，結合表1所示參數可知，該最好解開放了最少數量的配送中心、最少的數量中轉站，使用了最小數量的車輛。因此，該解的質量較好。

表3 不同算法求解效果比較1）

圖2 算例“3-7-65”最好解“3 220”的網絡結構

5 結束語

針對城市物流配送中的兩級定位-路徑問題，建立了相應的數學模型，并將求解NP-hard問題效果較好的人工蜂群算法應用于包括多個NP-hard子問題的兩級定位-路徑問題的求解；針對人工蜂群算法容易出現早熟的問題，在算法的鄰域搜索階段，根據變鄰域搜索思想提出了三種變鄰域搜索策略。仿真實驗結果表明，變鄰域人工蜂群算法能有效求解兩級定位-路徑問題；提出的三種變鄰域搜索策略各有優勢，可根據實際應用的需要及決策者的個人偏好，選擇相應的搜索策略。因此，實際應用時，可根據決策者的風險偏好進行選擇。若決策者為風險回避者，應選擇基于變鄰域搜索策略S2的人工蜂群算法進行求解，以期得到更優的最差解；若決策者為風險中立者或風險追求者，應選擇基于變鄰域搜索策略S1的人工蜂群算法進行求解，以期得到更優的平均解或最好解。此外，若在某些更關心決策效率的應用情形，如應急物流等，則應選擇基于變鄰域搜索策略S3的人工蜂群算法進行求解，以期在更短時間內求得滿意解。

[1]NagyG，Salhi S.Location-routing：issues，models and methods[J].European Journal of Operational Research，2007，177（2）：649-672.

[2]Jacobsen S K，Madsen O B G.A comparative study of heuristics for a two-level routing-location problem[J].European Journal of Operational Research，1980，5（6）：378-387.

[3]Ambrosino D，Sciomachena A，Scutellàb M G.A heuristic based on multi-exchange techniques for a regional fleet assignment location-routing problem[J].Computers&Operations Research，2009，36（2）：442-460.

[4]Sterle C.Location-routing models and methods for freight distribution and infomobility in city logistics[D].Universita Degli Studi di Napoli“Federico II”，Naples，Italy，2010.

[5]Li Jin，Zhu Y，Shen H，et al.A hybrid genetic algorithm for two-layer location-routing problem[C]//4th International Conference on New Trends in Information Science and Service Science（NISS），2010：642-645.

[6]Boccia M，Crainic T G，Sforza A，et al.A metaheuristic for a two Echelon Location-Routing Problem[C]//Lecture Notes in Computer Science.Berlin Heidelberg：Springer-Verlag，2010：288-301.

[7]王紹仁，馬祖軍.震害緊急響應階段應急物流系統中的LRP[J].系統工程理論與實踐，2011，31（8）：1497-1507.

[8]Nguyen V P，Prins C，Prodhon C.Solving the two-echelon location routing problem by a GRASP reinforced by a learning process and path relinking[J].European Journal of Operational Research，2012，216（1）：113-126.

[9]Nguyen V P，Prins C，Prodhon C.A multi-start iterated local search with tabu list and path relinking for the two echelon location-routing problem[J].Engineering Applications of Artificial Intelligence，2012，25（1）：56-71.

[10]Karaboga D.An idea based on honey bee swarm for numerical optimization，TR06[R].Kaayseri：Erciyes University，2005.

[11]暴勵.人工蜂群算法的混合策略研究[D].太原：太原科技大學，2010.

[12]胡大偉.設施定位和車輛路線問題模型及其啟發式算法研究[D].西安：長安大學，2008：129-133.

[13]李曉磊.一種新型的智能優化方法——人工魚群算法[D].杭州：浙江大學，2003.

[14]董偉.變鄰域搜索算法研究及在組合優化中的應用[D].阜新：遼寧工程技術大學，2011：1-2.

CHEN Jiumei1，2,GONG Ying1，2

1.Chongqing Key Laboratory of Electronic Commerce&Supply Chain System,Chongqing Technology and Business University,Chongqing 400067,China
2.Strategical Planning Department,Chongqing Technology and Business University,Chongqing 400067,China

A mathematical model of two-echelon location-routing problem is established.Artificial Bee Colony algorithm is put forward to solve this problem.Since this algorithm usually has premature convergence.Variable neighborhood search, a novel path heuristic algorithm appearing abroad in recent years,is blended in this algorithm.At the same time,three kinds of variable neighborhood search strategy are put forward.The comparison simulation between Artificial Bee Colony algorithm with different variable neighborhood search strategies and artificial fish swarm algorithm has been done.The experimental results show that Artificial Bee Colony algorithm with variable neighborhood search can effectively solve two-echelon location-routing problem.

two-Echelon Location-Routing Problem（2E-LRP）;Artificial Bee Colony（ABC）algorithm;Variable Neighborhood Search（VNS）;logistics;distribution

A

F224.3

10.3778/j.issn.1002-8331.1309-0335

CHEN Jiumei,GONG Ying.Artificial Bee Colony algorithm with variable neighborhood search for two-Echelon Location-Routing Problem.Computer Engineering and Applications,2014,50（6）：25-30.

國家自然科學基金（No.71101159）。

陳久梅（1976—），女，博士，副教授，研究領域為物流系統優化、智能算法等；龔英（1968—），女，教授，研究領域為物流與供應鏈。E-mail：chenjiumei@163.com

2013-09-23

2013-11-10

1002-8331（2014）06-0025-06

CNKI網絡優先出版：2013-11-15，http://www.cnki.net/kcms/detail/11.2127.TP.20131115.1121.009.html