基于虛擬目標的KKV逆軌攔截導引方法

舒健生，孟少飛，張士熊

(第二炮兵工程大學906 室，西安 710025)

逆軌攔截是一種特殊的攔截方式，它要求攔截器要在與目標遭遇之前飛到目標正前方的軌道上，并以較小的軌道交角與目標遭遇。這種攔截方式具有較大的攔截概率［1］，同時也能提高攔截高速非機動目標的攔截精度［2］，但同時也需要已知目標的運動狀態信息［3］。考察逆軌攔截的軌道可以看出，逆軌攔截時攔截器的速度方向往往指向衛星軌道的延長方向上，并逐漸向衛星方向轉動，在這個過程中，攔截器的位置也逐漸向衛星軌道的延長線靠近，并最終沿著衛星軌道的延長線飛向衛星。因此可以假設存在一個鏡像目標T'，其飛行方向與真實目標T 相反，并最終與真實目標逆向相遇。而攔截器的飛向過程可以看做是以這個鏡像目標為導引的追蹤過程，如圖1 所示。在這個思路基礎上，本文設計了基于組合預測命中點的逆軌攔截導引方法。

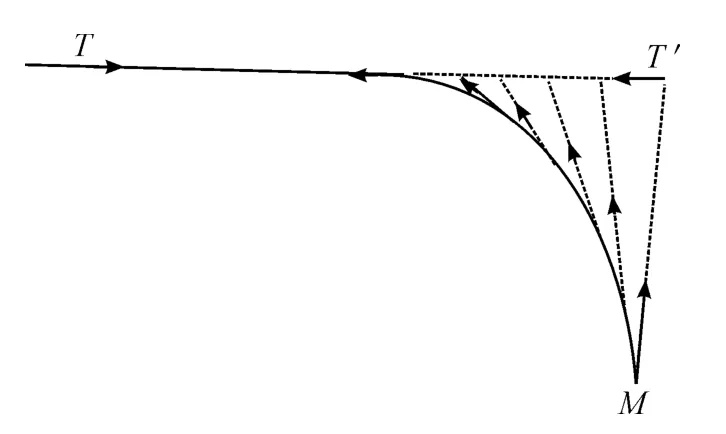
圖1 虛擬目標示意圖

1 虛擬目標的確定

設初始時刻目標在慣性空間的運動參數為RT(t)、VT(t)，在較短時間Δt 內，其在慣性空間的運動可以當做“二體問題”來看待。則其Δt 時間后的運動參數可以進行預測

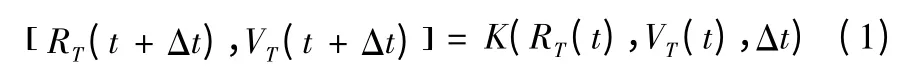
其中K(·)為開普勒方程的解算過程。令Δt = Δt1+ Δt2，則有:

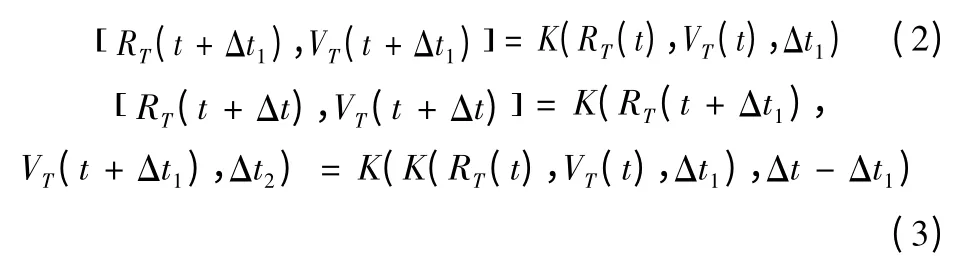
設剩余時間為tgo，由于沿視線方向上的相對速度的變化率較小，因此tgo可用下式進行估計

對式(4)導有

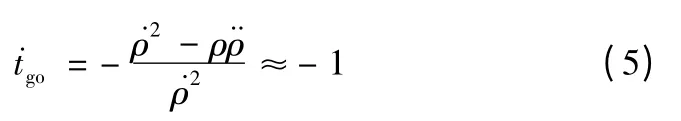
假設預測命中點為m*，其對應的空間位置為R*(t)，則R*(t)為目標軌道上的點，且有

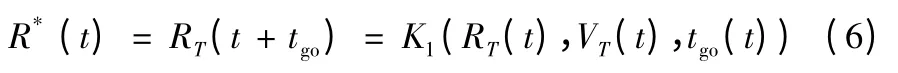
其中K1(·)表示取結果的第一項，tgo(t)為t 時刻的剩余時間。經過較小的時間τ 后，預測命中點的位置為

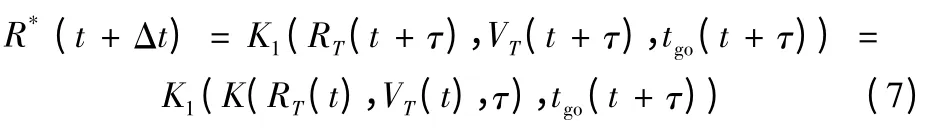
又有

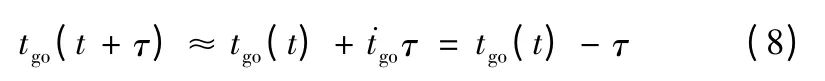
代入式(7)可得

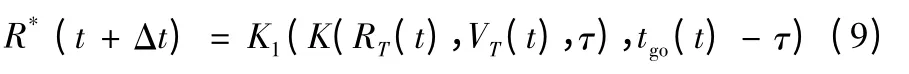
結合式(3)有

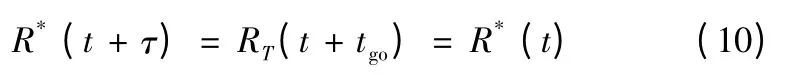
所以m*的移動速度為

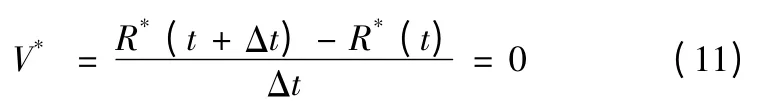
記目標在m*點的速度為，則有

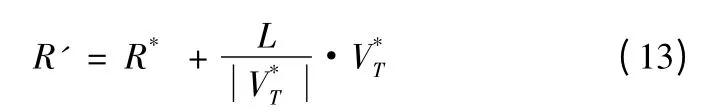
假設T'以恒定的速度向m*靠近，并在tgo時間內到達m*。記其速度為V'，則有

將式(14)代入式(15)可得

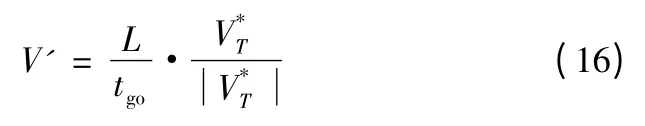
2 導引方法的選擇

考慮到T'運動特點是以恒定的速度和方向向m*運動，并以逆軌的方式與衛星遭遇。如果攔截器能在T'正后方尾隨T'飛行，并在tgo時間內追上T'點，則攔截器就能實現對衛星的逆軌攔截。

追蹤法是一種控制攔截器的速度方向始終指向目標的導引方法，在視線坐標系下導引律［4］

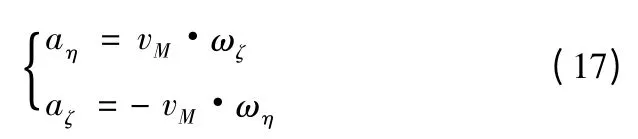
追蹤法特點是攔截器在任何起始射角下，都會從目標正后方命中目標。因此，可以用追蹤法導引攔截器飛向T'，從而實現從正后方命中T'，對衛星逆軌攔截的目的［5］。

在飛行過程中，攔截器為了跟蹤衛星的運動，其導引頭始終是對準目標的。而以T'點作為虛擬目標對攔截器進行導引時，可以假設攔截器有一個虛擬視場是對準T'點的，其與T'點的連線即為虛擬視線LOVS(Light Of Virtual Sight)，導引律的解算依賴的是從攔截器到m'點的虛擬視線的信息q'ε、q'β和

當已知T'的位置R'時，攔截器與T'的相對運動狀態為

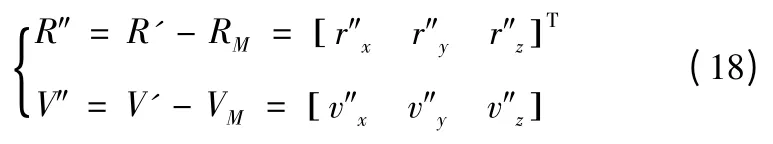
攔截器與T'的距離為

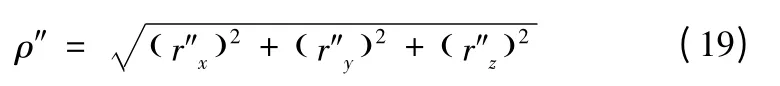
則虛擬視線的高低角和方位角q'ε、q'β分別為

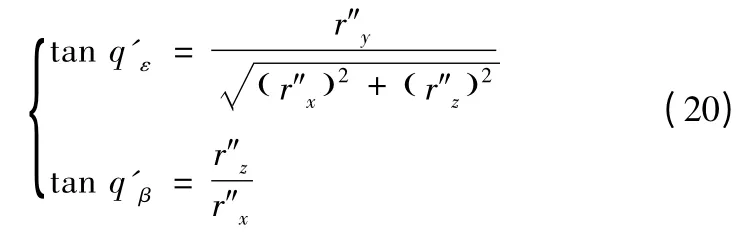
慣性坐標系和由虛擬視線構成的虛擬視線坐標系的轉換矩陣為

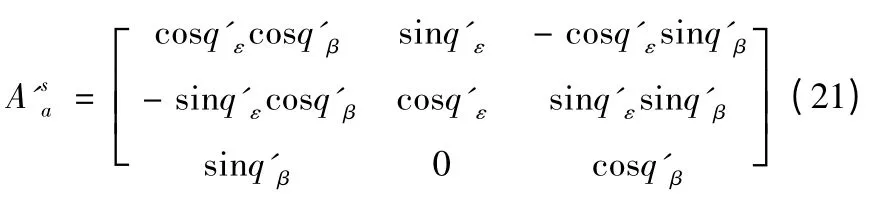
設攔截器和T'點的相對速度轉換到虛擬視線坐標系中為V's，則有

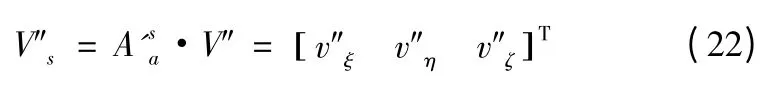
則虛擬視線的轉率為

記攔截器的初始速度轉化到虛擬視線坐標系中為V'Ms0，則有

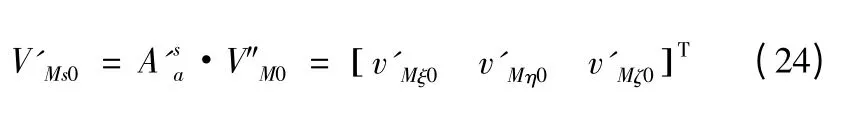
由于初始速度往往不是沿著虛擬視線方向的，因此有v'Mη0≠0，v'Mζ0≠0，因此需要在導引律中加入修正項，使v'Mη→0，v'Mζ→0。設計虛擬視線坐標系下的導引律為

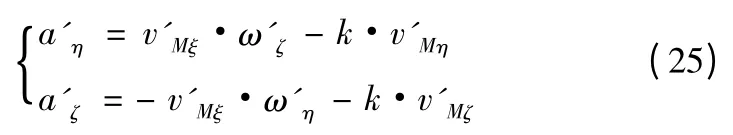
當攔截器和T'點的距離小于一定值時，T'點的誤差和移動對視線轉率影響增大，此時，攔截器開始以真實目標進行導引。

3 L 取值范圍的討論

追蹤法的飛行時間為［6］

其中，ρ'為攔截器和T'點的距離;V'為T'的速度的大小，有V' =;q 為虛擬視線和m'運動軌跡的夾角，即也是虛擬視線和V'的夾角。

為了使攔截器在到達T'的同時，T'也到達m*，需要使T=tgo，同時將式(14)代入式(26)可得方程

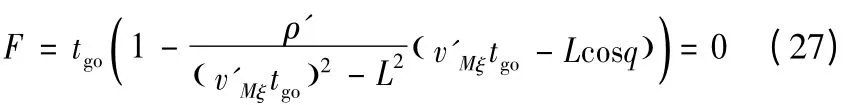
式(27)是一個關于L 的超越方程，難以求得解析解。

設攔截器和目標的初始距離為315 km，接近速度為10 km/s，計算不同L 值下F 的值，進而得到F 隨L 的變化規律如圖2 所示。

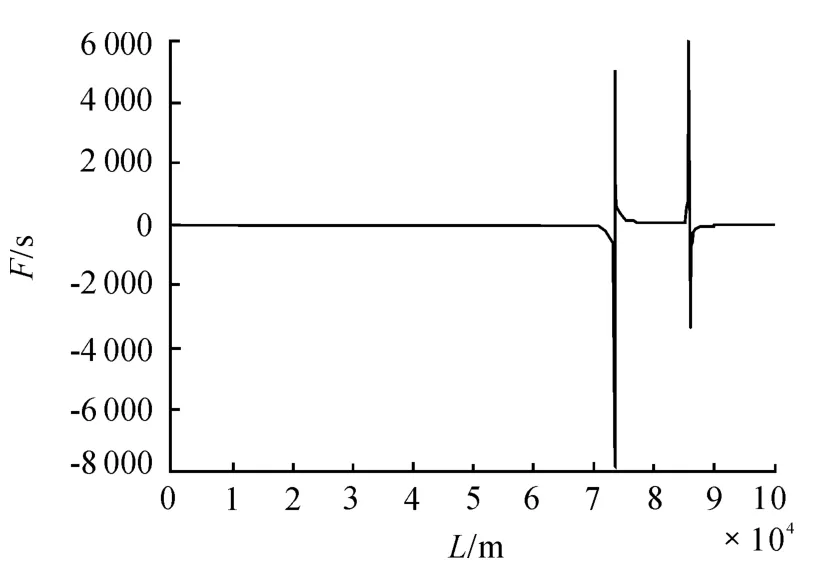
圖2 F 隨ρ'的變化規律

可以看出，F 并不是隨L 單調變化，因此也難以用數值方法求解方程(4.53)。但是從圖中可以看出，L≤70 km 時，F 的值基本保持在0 附近，可以近似作為式(27)近似解的范圍。

4 推力的轉化

加入預測命中點后求得的推力加速度a'η、a'ζ是相對于虛擬視線的法向和側向的加速度，實際上，攔截器的視線始終是對準真實目標的，其提供的推力加速度也是沿著真實視線的法向和側向的。因此，需要計算真實視線坐標系中與a'η、a'ζ等效的推力加速度aη、aζ。

考慮到真實視線坐標系中的推力在沿視線方向上為零，但變換到虛擬視線坐標系后沿虛擬視線方向卻不再是零，只能保證在虛擬視線的法向和側向上的分量和計算值相等。因此可以設其沿著虛擬視線的分量為a'ξ，則在虛擬視線坐標系中推力加速度為，其轉換到發射慣性坐標系中有

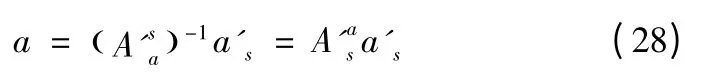
同時，將發射慣性坐標系下的推力加速度轉換到真實的視線坐標系中有

聯立式(28)和式(29)有

由于qε、qβ和q'ε、q'β都是已知的，因此的值也可以計算得到，在這里將表示為A，即

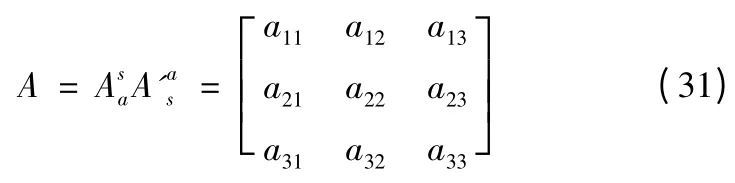
因此式(30)又可以表示為

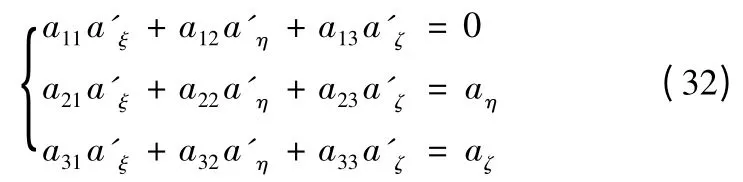
由上式第一項可以解得

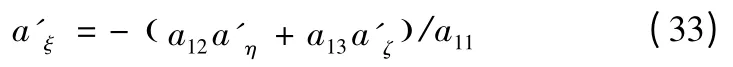
將其代入式(32)后兩項則可求得實際視線坐標系下的推力加速度為

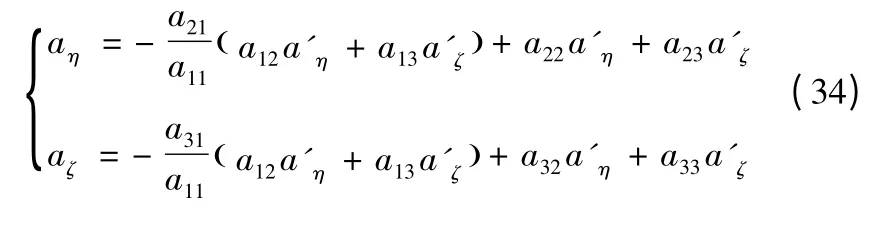
5 仿真驗證

假設末端初始時刻，攔截器和衛星的初始距離為315 km，接近速度為10 km/s，目標速度為7.036 71 km/s，攔截器速度為3.001 75 km/s。攔截器質量為30 kg，最大軌控加速度為10 g0，取L=20.0 km。

仿真結果顯示脫靶量為0.399 536 m，三維效果如圖3和圖4 所示。

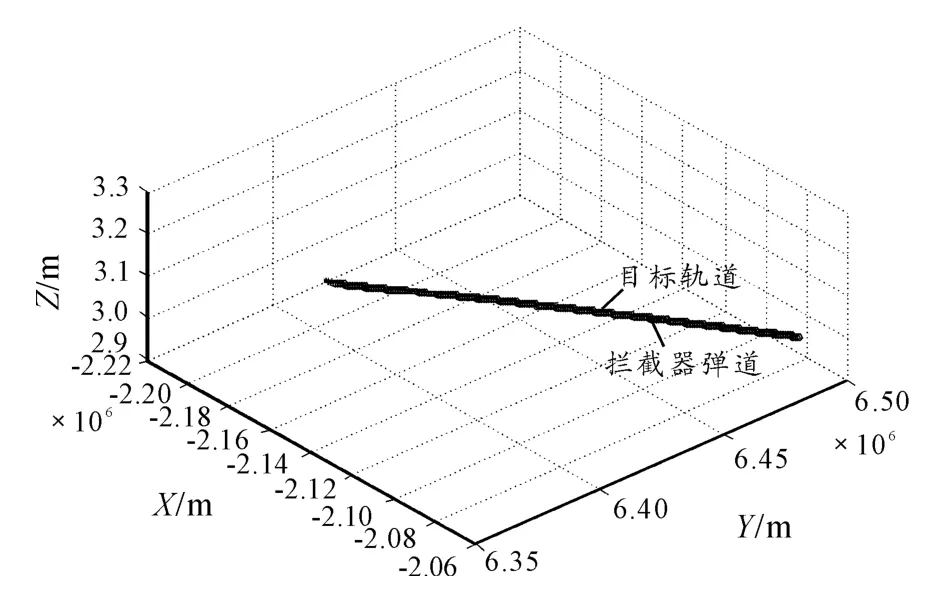
圖3 仿真效果圖

圖4 攔截器彈道放大圖

由圖3 可以看出，攔截器的彈道呈現弧度較小的“S”形，比較平直。由圖4 可以看出，攔截器的彈道中間平直，兩頭有較小的弧度。攔截初始階段，攔截器向遠處的T'飛向，由于距離ρ 較大，虛擬視線轉率較小，因此攔截器的速度方向變化較小，彈道比較平直。當接近T'點時，視線轉率增大，速度也轉動較快，于是在末端附近彈道比較彎曲。視線轉率隨時間的變化如圖5 所示。

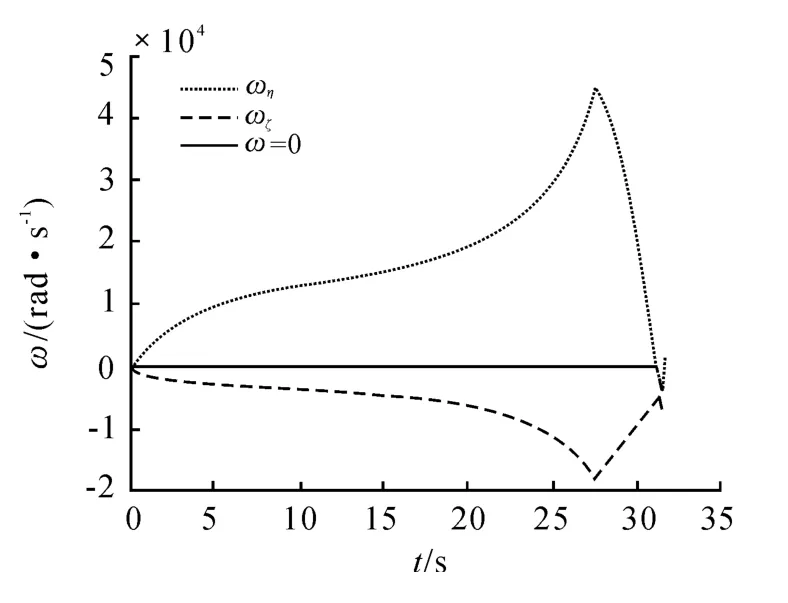
圖5 視線轉率變化圖

由圖5 可以看出，視線轉率的變化分為兩個階段，第一階段是攔截器向T'的迅速靠近過程，這個過程中由于ρ 較大，虛擬視線轉率小，攔截器的速度方向變化小，視線轉率主要由衛星的法向速度決定，并逐漸增大。隨著攔截器逐漸靠近T'，虛擬視線轉率增大，攔截器的速度方向變化較大，抑制了視線的增大，并隨著逆軌的逐漸完成，視線轉率逐漸減小，并收斂到零附近。最后隨著ρ 的減小，視線轉率發散。

6 結束語

本文以真實目標運動參數和剩余時間求解出虛擬目標的運動參數，并以低速勻速運動的虛擬目標代替高速變速的真實目標對攔截器進行導引。在導引方法的選擇上利用力追蹤法總是從目標后方靠近目標的特性，來實現逆軌攔截的目的，并且比較簡單與穩定。最后的仿真結果驗證了這種方法的可行性，由仿真結果來看，攔截器彈道較為平滑，脫靶量較小。

［1］王繼平，鮮勇，王明海，等.軌道交角與時間偏差對攔截衛星攔截概率的影響［J］. 飛行力學，2008，26（5）:89-92.

［2］胡小磊.反導逆軌攔截復合制導律研究與仿真［J］.空軍裝備研究，2010，4（1）:20-23.

［3］吳鵬.帶末段攻擊角約束的制導方法研究［D］.哈爾濱:哈爾濱工業大學，2009.

［4］雷虎明.導彈制導與控制原理［M］.北京:國防工業出版社，2006.

［5］劉興堂.導彈制導控制與系統仿真［M］.西安:西北工業大學出版社，2006.

［6］程國采.戰術導彈導引方法［M］.北京:國防工業出版社，1996.