基于電路模型的彈射用永磁無刷直流直線電機參數優化及仿真

湯子鑫，姬新陽，孫思浩，林煒庭

(1.總裝備部南京軍事代表局 駐福州地區軍事代表室，福州 350003;2.中國洛陽電子裝備試驗中心，孟州 454750)

電磁彈射［1-3］用永磁無刷直流直線電機在工作過程中，電壓高、電流大，要求推力恒定，速度動態范圍大，末速度能達到幾十甚至上百米每秒，對推力波動、位置精度要求相對較低。因此，電磁彈射用直線電機參數的選擇，要結合電磁彈射的特點，在傳統的方法基礎上進行改進、修正。

文獻［4］中采用有限元的方法對轉矩波動進行優化，對于彈射用電機，難度增大，考慮的因素更多。對推力波動的分析，考慮電機工作在穩態，速度是恒定的，沒有考慮速度的影響，不適合用于彈射用電機分析［5-6］。文獻［7-9］中對推力波動進行了優化，采用的控制算法并未深入分析速度對推力的影響，其控制在低速效果較好，在高速時還需改進，并且在高速時閉環控制可能因為換相時間過長而不能使用。

文中結合電磁彈射的特點，推導出換相推力波動、非換相期間推力波動、效率公式，并以此為目標函數建立了矢量優化模型。采用詞典排序算法解決了多目標之間沖突問題，對單個目標函數采用模擬退火算法進行優化求解，最后在Matlab 環境下進行了仿真驗證。

1 永磁無刷直流直線電機數學模型

永磁無刷直流直線電機采用方波供電，三相星型六狀態工作方式。為方便分析，作如下假設:

1)三相對稱，反電動勢為梯形波，平頂部分等于120°電角度;

2)忽略電樞反應、齒槽效應、端部效應和磁路飽和的影響;

3)相繞組的等效電感為常數;

1.1 換相過程的數學模型

換相過程［10］以A 相為例，從A 相關斷開始，到A 相電流降為零，此過程的等效電路如圖1 所示。

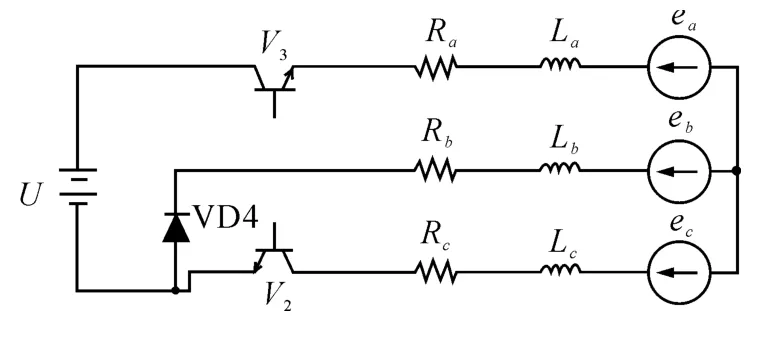
圖1 換相期間電機等效電路

在換相期間，直線電機的數學模型為

在B/C 相導通的換流過程中，三相繞組的反電動勢分別為

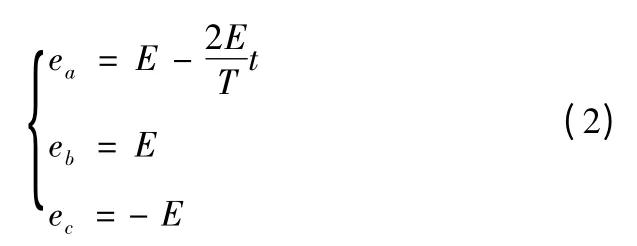
其中E=kv，k 為繞組反電動勢系數。

其中R 表示繞組電阻，ia、ib、ic分別表示相電流，L 表示繞組等效電感，u 為端電壓。

永磁無刷直流直線電機的推力方程為

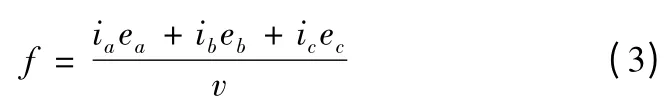
推力波動定義為

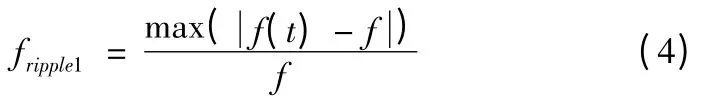
其中f(t)為換相期間的推力，f 為彈射過程要求的推力。

聯合式(1)～式(4)得到換相推力波動為

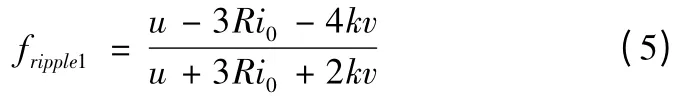
1.2 非換相過程數學模型

在非換相期間，任意時刻只有兩相導通，第三相截止。導通兩相繞組上的反電動勢大小相等，方向相反;電流大小相等，方向相反。不考慮非導通相續流的影響，采用PWM 調制方式，以A、B 兩相導通為例，其等效電路如圖2 所示。

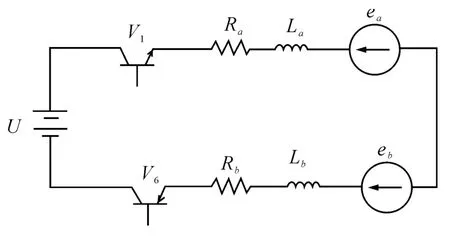
圖2 簡化的等效電路

其數學模型為

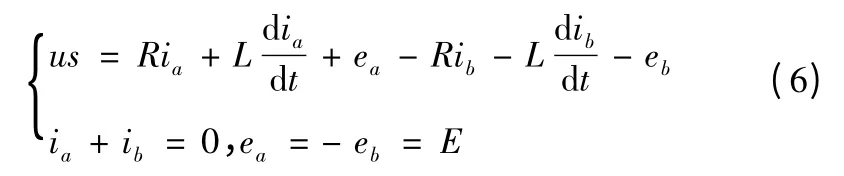
當PWM 信號為ON 時，s =1;當PWM 信號為OFF 時，s=0。u 為端電壓，v 為電機運動速度，反電動勢與速度的關系E=kv，k 反電動勢系數。

結合永磁無刷直流直線電機非換相期間推力波形特點，定義推力波動為

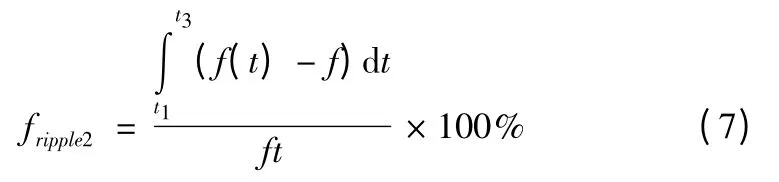
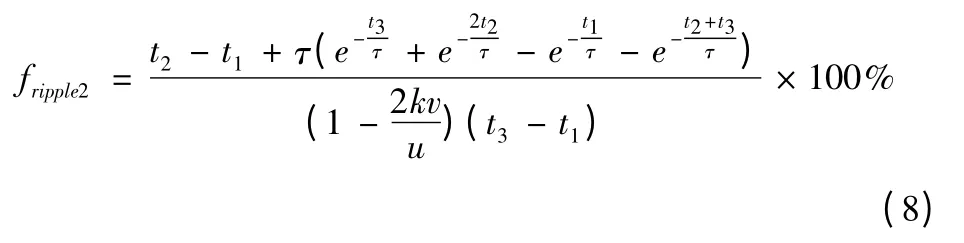
結合式(6)和式(7)得其中，推力波動的計算在一個PWM 周期下，對應的時間區間為［t1，t3］，PWM 信號為OFF 時對應的區間［t1，t2］，PWM 信號為OFF 時對應的區間為電磁時間常數。

2 彈射過程電流、電壓分析

在換相期間，其初始電流為非換相期間結束時的電流，因此換相期間初始電流為換相時間很短，假設在換相期間電壓大小不變，電壓大小為非換相結束時的電壓。

將式(9)和式(10)代入換相期間推力波動式(5)和非換相期間推力波動式(8)，得到在電磁彈射過程中的推力波動公式分別為

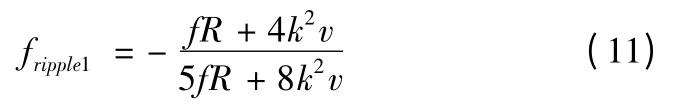
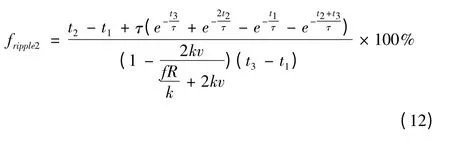
3 電機參數優化

對于優化問題，從3 個方面進行分析，目標函數、約束條件、最優解的計算方法。

3.1 目標函數的確定

對于非換相期間推力波動，推力增大，推力波動減小，速度增大，推力波動增大。因此，只選一組推力和速度是不能代表整個系統的推力波動。為了能更好地反應速度和推力對換相推力波動的影響，選擇多組推力和速度。以多組推力和速度的換相推力波動之和作為優化目標函數

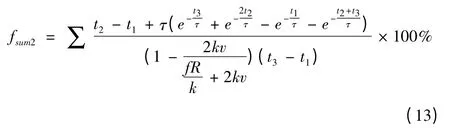
換相推力波動的分析方法與非換相期間推力波動類似，以多組推力和速度的換相推力波動之和作為優化目標函數

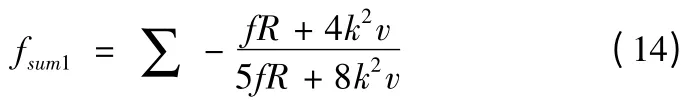
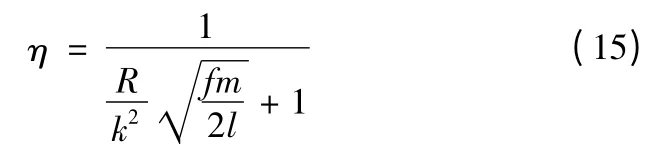
以電機效率最高為第三個目標函數。

3.2 約束條件

換相過程中，任何速度下的換相推力波動要滿足系統的要求，即

在非換相過程中，同時對于每個速度，推力波動要滿足系統的要求

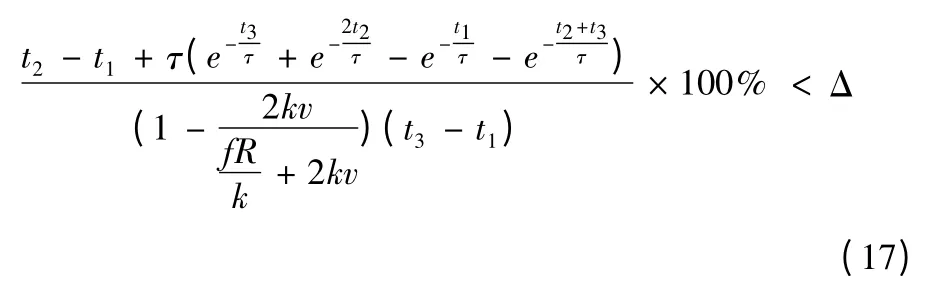
其中Δ 為系統要求的推力波動大小。

在電磁彈射過程中，由于受器件及各種因素的影響，電流和電壓的大小被受到限制，因此工作電流和電壓要小于系統的要求。

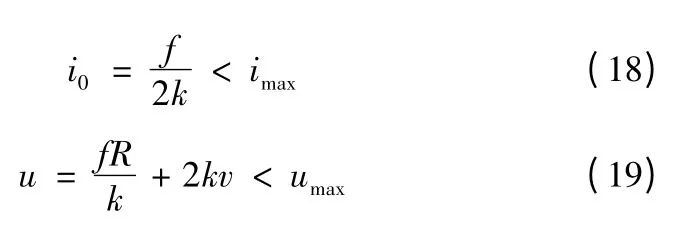
在實際中，各相參數的取值是受到限制的，為了減小計算量，獲得優化的解，對電感、電阻、反電動勢系數進行約束，根據實際情況，給出電感、電阻、反電動勢系數的數值范圍

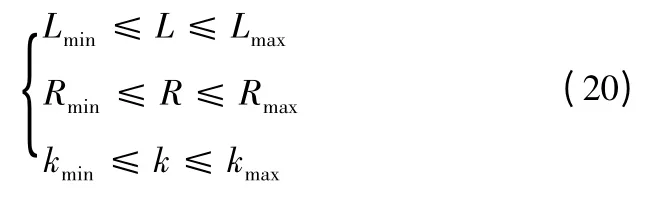
3.3 參數求解

對于矢量優化問題，解決的方法很多，如加權極小極大最優值法、基于性別辨識的矢量遺傳算法、詞典排序算法、隨機權系數和優等個體法、基于接觸理論確定Pareto 最優解方法等。在文中采用詞典排序算法(Lexicographic Ordering)，其原理是根據目標函數的重要性進行排序，先對最重要的目標函數進行尋優，然后根據目標函數的重要性依次進行，最終求的最優解。

本文中的3 個目標函數，重要性依次為非換相期間推力波動最小、換相推力波動最小、效率最高。對于每一個目標函數，對應的優化模型屬于非線性優化問題，一般的解析方法過于復雜。可采用粒子群、模擬退火、遺傳算法等智能隨機搜索算法，在本文中采用模擬退火算法。

Metropolis 等人在1953 年提出了模擬退火算法Simulated Annealing Algorithm(SA)，基本思想是把優化過程與統計熱力學的熱平衡問題進行對比，固體退火過程的物理圖像和統計特性是模擬退火算法的物理背景，Metropolis 接受準則使算法跳離局部最優的陷阱，冷卻進度表的合理選擇是算法應用的前提。固體退火是先將固體加熱至溶化，然后徐徐冷卻使之凝固成規整晶體的熱力學過程。具體算法實現過程如下:

1)以最小非換相期間推力波動為目標函數，采用SA 進行優化;

2)以最小換相推力波動為目標函數，利用第一步中求的最優解，將非換相期間推力波動等于該最小值作為約束條件，采用SA 進一步優化;

3)以最高效率為目標函數，將第二步中最小換相推力波動等于最小值作為約束條件，其他約束條件不變，利用SA求得最優解，此時的最優解為矢量優化目標的最優解。

對于每一個目標函數f(x)的優化，采用模擬退火算法，具體過程如下:

1)參數初始化，首先給出被優化參數(電阻、電感、反電動勢系數)的取值范圍，即解空間為= L，R，( )k ?[ LminLmax]× [ RminRmax]× [ kminkmax]。控制參數的初始值T 及衰減系數λ，內循環次數Ns，步長向量=［v1，v2，v3］，終止規則(精度值ε 及溫度最小值Tm);初始化搜索點x0，計算f0=f)，令=。

3)計算f ' =f(x')，如果f '≤fi，則接受新解，令如果f ' ＞fi，以概率p = exp接受新點x'(Metropolis 準則)，在新解'被接受的情況下，令

4)h=h+1，如果h ＜Ns，轉到步驟2，否則h=1，轉到下一步。

5)減小控制參數Tk+1=λTk，如果Tk+1＜Tm，則算法終止，否則重復步驟2)到4)。

4 參數優化與仿真

電機參數優化時選擇推力分別為1 500 N、2 000 N、2 500 N、3 000 N、3 500 N、4 000 N;速度取值選擇為5 m/s，10 m/s，15 m/s，20 m/s，25 m/s，30 m/s，35 m/s;非換相推力波動要求小于10%，換相推力波動要求為小于30%，因為換相推力波動還可以通過各種控制方法進一步減小，而非換相推波動要進一步減小非常復雜;最大電流為imax=300 A，最大電壓umax=1 500 V;電感參數區間 2，[ ]20 ，單位mH，電阻取值區間 1，[ ]10 ，單位Ω，反電動勢系數的取值 5，[ ]20 ，單位V×s/m，占空比0.9。

分別以非換相推力波動、換相推力波動、效率為目標函數進行優化，計算結果如下:

以非換相期間的推力波動為目標函數，得到最優參數為:r=3.429，k=8.247，L=5.87;

以換相期間推力波動為目標函數得到最優參數為:r =6.533，k=5.122，L=18.2;

以效率為目標函數，優化后得到:r =1.636，k =12.551，L=7.13。

其中，以效率為目標函數得到的參數即為矢量目標函數的最優參數，所以電機的最優參數為r =1.636，k =12.551，L=7.13。

為了驗證理論分析的正確性，以負載30 kg，推力2 000 N，末速度要求35 m/s，加速距離為其效率為對位移區間5 ～5.5 m 進行推力仿真。

圖3 為未進行抑制時的換相推力波動，推力波動達到20%。采用提前換相抑制方法，換相推力波動減小到10%以內，如圖4。

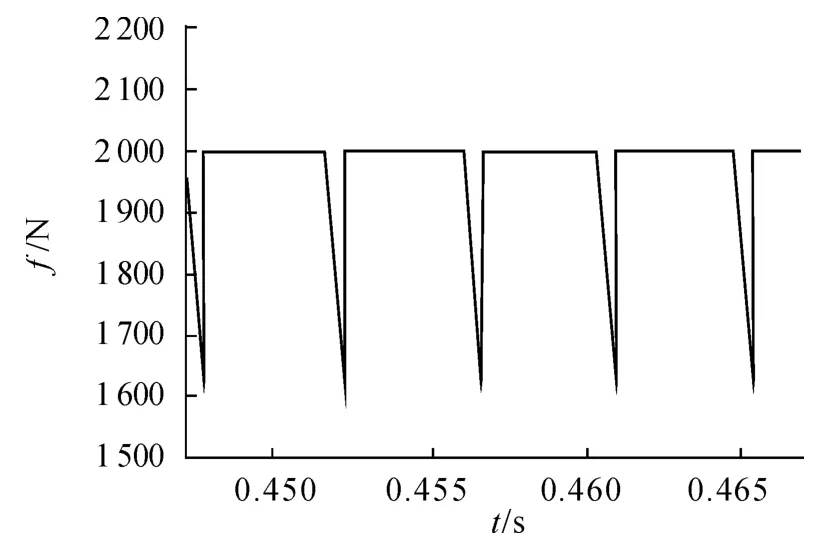
圖3 直接換相時的推力

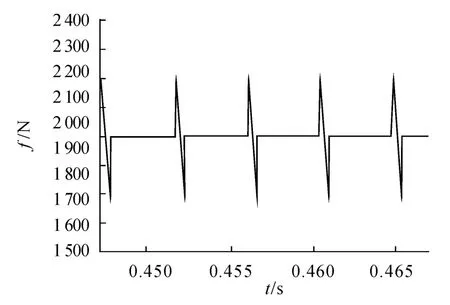
圖4 抑制后的換相推力

圖5 是電機在5 ～5.5 m 時的推力曲線，其中非換相期間推力波動較小，而換相推力波動較大，所以在對推力波動抑制中，重點考慮換相推力波動。

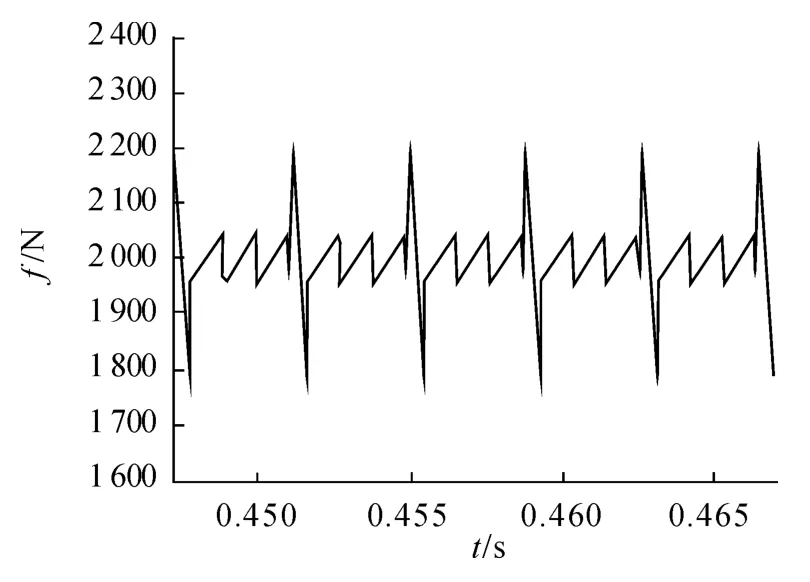
圖5 5 ～5.5 m 的推力曲線

5 結束語

在換相期間和非換相期間數學模型基礎上，推導出推力波動公式。結合電磁彈射的特點，分析得到換相期間和非換相期間以推力和速度為自變量的電流及電壓表達式。并將電流電壓公式代入到非換相推力波動、換相推力波動及效率的表達式，得到新的表達式，并依此為目標函數，建立矢量優化模型。采用詞典排序法解決多目標之間的沖突問題，對于每一目標函數的優化，采用模擬退火算法。求解模型獲得電機參數，并通過MATLAB 仿真驗證了理論分析的可行性，從得到的結果中看出，電機本體優化對換相推力波動減小是有限的，還需通過電機控制進一步減小換相推力波動以滿足系統的要求。

［1］李立毅，李小鵬.電磁發射的歷史與發展趨勢［J］.微電機，2004，37（1）:41-44.

［2］Doyle M，Sulish G，Lebron L.The benefits of electromagnetically launching aircraft［J］. Naval Engineering Journal，2000，112（3）:77-82.

［3］吳始棟.美國海軍電磁彈射器現狀［J］.船電技術，2005（3）:5-6.

［4］Ohnishi T，Takahashi N. Optimal design of efficient IPM motor using finite element method［J］.IEEE Trans.Magn.，2000，36:3537–3539.

［5］S. M. Hwang，D. K. Lieu. Reduction of torque ripple in brushless DC motors［J］.IEEE Trans.Magn，1999，31（2）:3737-3739.

［6］Min Dai，Ali Keyhani. Torque ripple analysis of a PM Brushless DC Motor using finite element method［J］.IEEE transaction on energy conversion，2004（19）:40- 45.

［7］Zhu Z Q，Howe D.Influence of design parameters on cogging torque in permanent magnet machines［J］. IEEE Trans.Energy Conversion，2000（15）:407–412.

［8］Yong Liu，Zhu Z Q，David Howe. Direct torque control of brushless DC drives with reduced torque ripple［J］. IEEE transaction on industry applications2005，41（2）:599-608.

［9］Xia C L，Guo P J，Shi T N，Speed control of brushless DC motor using genetic algorithm based on fuzzy controller［C］//IEEE international conference on intelligent mechanics and Automation Japan.［S. l.］:［s. n.］，2004: 460-464.

［10］Zhu Z Q.Direct torque control of brushless DC drives with reduced torque ripple［J］.IEEE transactions on industry applications，2005，41（2）:599-605.