基于改進的距離判別分析法的電火工品感度性能預測方法

崔偉成，孫玉玉，劉林密，孟凡磊

(海軍航空工程學院 a.飛行器工程系;b.政治部，山東 煙臺 264001)

感度是電火工品的重要性能參數，通常采用感度上下限測試、升降法感度試驗或感度曲線的方法判斷整批電火工品的感度性能，目前還沒有成熟的單發電火工品感度性能的預測方法。瞬態脈沖法是一種對電火工品無損檢測的方法，通過瞬態脈沖法可得到溫升、升溫常數、熱散失系數及熱容等熱參數。由熱參數預測單發電火工品的感度性能，是一個可取的方案［1-5］。

文獻［1］通過試驗研究了電火工品的熱參數與感度性能之間的關系，指出:溫升、升溫常數能顯著反映電火工品的感度性能，可選用兩者之一作為感度性能判斷的依據。其不足是無顯著性分析過程;分類精度不高;無量化指標，通用性不強。為了充分挖掘試驗數據，研究電火工品的熱參數與感度性能之間的關系，本文對熱參數進行方差分析，然后選取合適的熱參數作為特征量，并基于改進的距離判別分析法對電火工品的感度性能進行預測。

1 方差分析

為了定量分析熱參數對電火工品感度性能影響的顯著性，采用方差分析的方法處理文獻［1］的試驗結果。假定熱參數對感性性能的影響相互獨立，運用單因素方差分析法，將試驗數據分成兩組:發火的電火工品為總體1，試驗次數為r1，不發火的電火工品為總體2，試驗次數為r2。由每個熱參數的數據生成4 個單因素試驗數據表，其格式見表1。

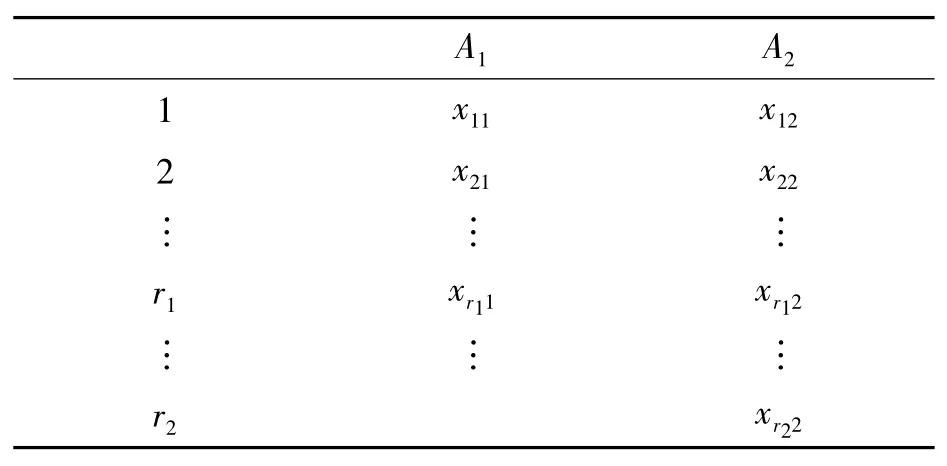
表1 單因素試驗數據表

表1 中:A1為總體1(發火)的某一熱參數;A2為總體2(不發火)的某一熱參數;xij為在第i 個水平(第i 個試驗)下第j 個總體的樣本。

檢驗統計量為

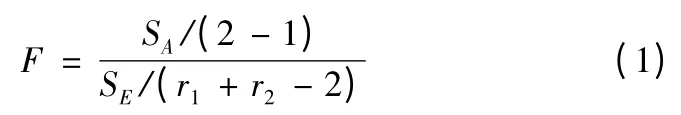
式(1)中:SA為各組數據均值對總方差的偏差平方和;SE為各組內數據對均值偏差平方和的總和。

若兩個總體的熱參數無顯著差異，檢驗統計量F 服從自由度為n1=2-1，n2=r1+r2-2 的F 分布。為檢驗差異的顯著性，給定顯著性水平α，并記F 分布的1-α 分位數為F1-α(n1，n2)，若F ＜F1-α(n1，n2)，認為兩個總體的熱參數無顯著差異。

計算出兩個總體的溫升、升溫常數、集總熱散失系數及熱容無顯著差異的概率分別為1.631 9 ×10-8、8.723 5 ×10-5、0.001 7、0.372 1，即在α =0.05 顯著性水平下，溫升、升溫常數及集總熱散失系數對電火工品的感度性能影響規律顯著。因此，本文選用上述3 個熱參數作為電火工品感度性能預測的特征量。

2 預測方法

距離判別分析法是以距離作為相似性度量根據所研究的個體的觀測特征量來推斷該個體所屬類型的一種統計方法。選取合適的相似性度量是距離判別分析的關鍵。馬氏距離不受量綱的影響，避免了多重相關性所造成的信息重疊，是一個有效的相似性度量［6］。標準的馬氏距離判別分析法只能進行等級分類，本文對其輸出值進行了改進，給出了一個新的感度性能指標。

2.1 標準的馬氏距離判別分析法

對于經過瞬態脈沖試驗及發火驗證試驗的電火工品，將其分為兩組:發火的電火工品為總體1，不發火的電火工品為總體2。假定兩個總體的熱參數向量均服從多元正態分布，則待測電火工品與兩個總體的馬氏距離為［6］

式(2)中:μ1、μ2為總體1 和總體2 的均值向量;Σ1、Σ2為總體1 和總體2 的協方差陣;x 為待預測電火工品的熱參數向量;d1(x)、d2(x)為x 與總體1 和總體2 的馬氏距離。

若d1＜d2則可判定x 屬于總體1，即發火;若d1＞d2則可判定x 屬于總體2，即不發火。

2.2 改進的馬氏距離判別分析法

標準的馬氏距離判別法只能得出單發電火工品發火或不發火的結論，信息量少，不能進行感度性能排序，不利于質量控制。為了得到單發電火工品感度性能的量化指標，應選擇合適的感度性能指標對標準馬氏距離判別分析法的輸出值進行改進。考慮以下兩點:單發電火工品發火的感度性能指標與不發火的感度性能指標的數值之和為1;感度性能指標與馬氏距離保持反比關系。即新的感度性能指標滿足:

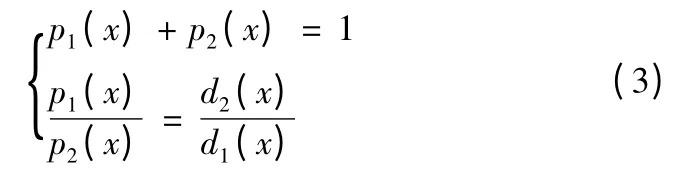
式(3)中:p1(x)為電火工品發火的感度性能指標;p2(x)為電火工品不發火的感度性能指標。本文以單發電火工品發火的感度性能指標作為討論對象:

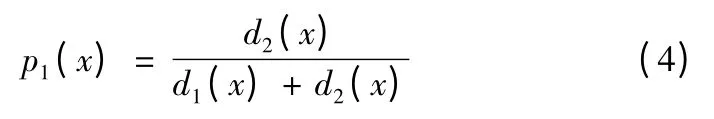
2.3 預測過程

單發電火工品感度性能預測過程:隨機選取一定量的電火工品作為學習樣本，分別進行瞬態脈沖試驗及發火驗證試驗。將試驗過的電火工品按發火與否分成兩類，取兩類電火工品的溫升、升溫常數及集總熱散失系數作為輸入向量，計算兩個總體的均值向量、協方差陣。對單發待測的電火工品進行瞬態脈沖試驗，由熱參數建立新的輸入向量，由式(2)、式(4)求出電火工品發火的感度性能指標。

3 實驗驗證

3.1 數據

3.2 預測

將發火的6 發產品作為總體1，未發火的24 發產品作為總體2，分別計算均值向量μ1和μ2，協方差陣Σ1和Σ2。將第1 發～第30 發產品的熱參數分別作為新的輸入向量x，預測每發產品發火的感度性能指標，結果見表2 的第5 列。表2 的第1 列為產品的試驗序號，各組數據按感度性能指標預測值從大到小降序排列。

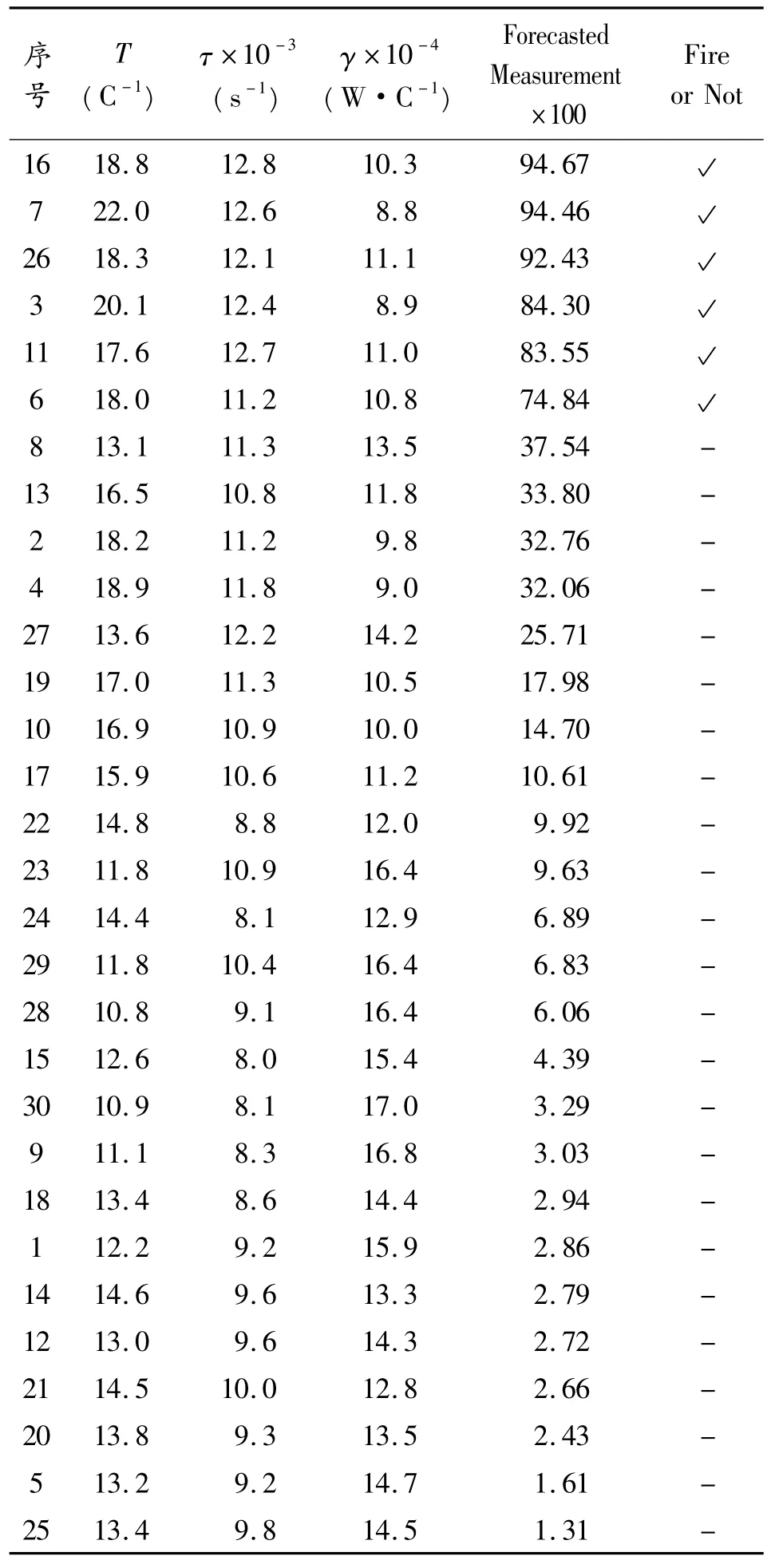
表2 第1 發～第30 發產品的試驗結果及預測結果

由表2 可以看出:感度性能指標排在前6 位的產品均發火，感度性能指標排在后23 位的產品均未發火，說明預測結果是可信的。第2 發、第4 發產品溫升均排在前6 位，集總熱散失系數均排在后6 位，以文獻［1］提出的“溫升越大，電火工品的感度越高”或“集總熱散失系數越小，電火工品的感度越高”作為依據，均會得出感度應排在前6 即發火的結論。但在發火驗證試驗中兩發產品并未發火，產生了誤判。本文考慮了第2 發升溫常數排在第11 位、第4 發產品升溫常數排在第7 位，即升溫常數均比較低的事實，融合了3 個熱參數的影響，得出兩發產品感度低的結論，與實際相符，說明本預測方法克服了以一個熱參數作為感度性能的分類依據所造成的精度較低、信息缺失的問題。

需要說明的是:預測方法是基于對試驗數據進行方差分析，并采用馬氏距離作為相似性度量而得出的，需要有足夠多的數據以保證統計學意義。僅從數值來看，感度性能指標預測值大于50%的產品均發火，低于50%的產品均未發火。該指標與產品的發火概率具有一定的類似性，能否認為兩者近似?這有待進一步研究。由方差分析的檢驗統計量可以看出熱參數對電火工品感度性能影響的顯著性是不一致的，尤其是集總熱散失系數對預測的貢獻率偏小，為了體現這一點應該在馬氏距離的基礎上加入特征量的權重［7-10］。本文將3 個特征量同等對待，實際上夸大了集總熱散失系數對預測的影響，但由于文獻［1］提供的數據偏少，也未造成誤判。下一步，應在增加試驗次數上的前提下以貢獻率為權值重新計算加權馬氏距離。

4 結束語

從結果來看，本文給出的感度性能指標能反映電火工品的感度性能，且預測精度高于以一個熱參數作為感度分類依據的方法，預測方法是可行的，感度性能指標與概率在數值上相似，具有一定的通用性。可通過以下兩個途徑進一步提高預測準確度:增加試驗次數;研究熱參數對感度性能影響的貢獻率。

［1］周彬，徐振相，秦志春，等.瞬態脈沖試驗中熱參數與電火工品發火性能的關系［J］. 火工品，2001，4（4）: 32-15.

［2］周彬. 橋絲式電火工品瞬態脈沖無損檢測技術研究［D］.南京:南京理工大學，2003.

［3］強濤，周彬，秦志春，等.橋絲式電火工品安全電流的預測［J］.南京理工大學學報，2006，30（1）:110-112.

［4］胡學先.電火工品小電流無損檢測的可行性［J］.含能材料.2003，11（1）:40-42.

［5］胡學先，胡軼. 電火工品的感度控制和預報. 火工品，1999（2）:39-42.

［6］袁志發，周靜芋. 多元統計分析［M］. 北京: 科學出版社，2002.

［7］Shen Hongbin，Yang Jie，Wang Shitong.Attribute weighted mercer kernel based fuzzy clustering algorithm for general non-spherical datasets［J］. Soft Comput，2006（10）: 1061-1073.

［8］蔡靜穎，謝福鼎，張永.基于馬氏距離特征加權的模糊聚類新算法［J］. 計算機工程與應用，2012，48（5）: 198-200.

［9］姚銀佩，李夕兵，宮鳳強，等.加權距離判別分析法在巖體質量等級分類中的應用［J］. 巖石力學與工程學報，2010，29（2）:4119-4123.

［10］趙琳，羅漢，劉京.加權馬氏距離判別分析方法及其權值確定——旅游信息服務系統的智能推薦［J］.經濟數學，2007，24（2）:185-188.