一類具有兩個邊界層現象的奇攝動邊值問題

葉珊珊，陳懷軍

（安徽師范大學 數學計算機科學學院，安徽 蕪湖 241000）

奇攝動邊值問題的一個顯著特征是小參數與最高階導數相乘，使得因變量在越過一個非常窄的區域時經受急劇的變化，并且這些窄的區域常常毗連感興趣區域的邊界，通常稱它們為邊界層.處理邊界層問題的方法有很多，其中包括：匹配漸近展開法、合成展開法以及多尺度方法［1－5］.例如在奇攝動邊值問題［5］.

當A，B為正常數時，退化方程y2＝0不滿足其中任何一個邊界條件，故在區間［0，1］兩端各有一個邊界層.利用匹配漸近展開法，需要在x＝0和x＝1附近將邊界層放大，通過引進適當的伸展變換分別求出內展開式，然后按照匹配原則將內展開式與外展開式進行匹配，得到在整個區間上一致有效的復合展開式.

本文考慮如下形式的奇攝動二階半線性邊值問題

其中ε＞0是小參數，n≥2為正整數，f（x）在區間［0，1］上連續且f（x）＞0，A和B為確定的正常數.先分析在區間［0，1］兩端可能出現邊界層現象的條件，利用直接匹配法（即Prandtl匹配原則）構造出在整個區間上一致有效的復合展開式，得到該問題具有邊界層性質的近似解.所做工作推廣了文獻［5］的結果.

1 主要結果

方程（1）中小參數與最高階導數相乘，退化方程為

因為f（x）＞0，A，B為正常數，退化方程（3）不滿足（2）中任何一個邊界條件，故在區間［0，1］兩端各有一個邊界層.我們先來尋找形式為

的外展開式.將（4）代入方程（1），并比較εo的系數，得y0（x）＝0，因此外部解yo～0.

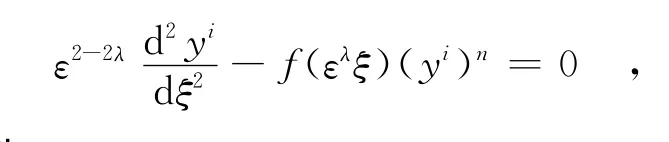
其特異極限對應于λ＝1，上式寫為

設

將（6）代入（5）和邊界條件（2）的第一式，并比較εo的系數得

分離變量并積分得

其特異極限對應于α＝1，上式寫為

設yI＝（ζ）＋L將它代入（10）和邊界條件（2）的第二式，并比較εo的系數得

因為

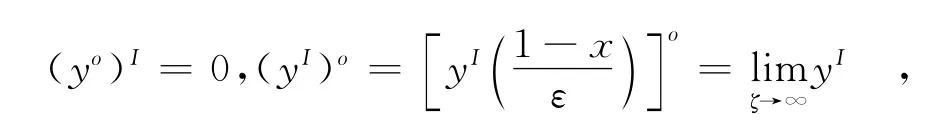
仍根據Prandtl匹配原則得到

. 于是類似上面的討論可得

最后把內、外兩展開式相加并減去其公共部分，便構成復合展開式的零次近似yc＝yo＋yi＋yI－（yi）o－（yI）o，即

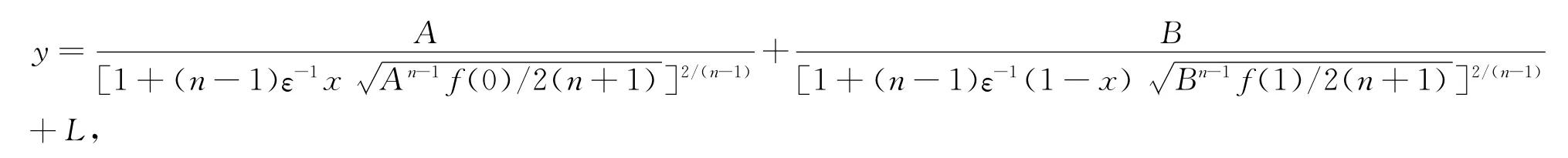
下面我們利用所得結果考慮兩個特殊情形.

Ⅰ.在問題（1），（2）中，取f（x）≡1，則邊值問題

的零次近似解為

Ⅱ.在問題（1），（2）中，取f（x）≡1，n＝2，則邊值問題ε2y″－y2＝0，0＜x ＜1，y（0，ε）＝A，y（1，ε）＝B，的零次近似解為

情形Ⅱ與文獻［5］所得結果是一致的.

2 小結

匹配漸近展開法的基本思想是一個問題的近似解雖然不能用單一尺度的展開式給出，但可先用不同尺度的展開式分別給出，它們分別在所考慮的部分區域內有效，這些部分區域的并覆蓋了所考慮的整個區域，然后再在內、外兩個展開式有效區域相互重疊的部分將它們匹配，使其構成一個在整個區域內有效的近似解.人們通常應用微分不等式理論和方法研究邊界層問題，通過分析微分不等式與相應的微分方程的解之間的關系，構造出一對適當的界定函數，在對所論問題的解作出先驗估計的同時，也證明了解的存在性.但該方法僅給出精確解與退化解之間的一個估計，未能構造出具有邊界層性質的近似解.利用匹配法則容易構造出邊值問題在整個區間上一致有效的復合展開式，從而得到更精細的精確解的近似式.

［1］ 劉樹德，魯世平，姚靜蓀，等.奇異攝動邊界層和內層理論［M］.北京：科學出版社，2012.

［2］ 陳懷軍，莫嘉琪.雙參數奇攝動非線性反應擴散問題［J］.物理學報，2010，59（7）：4 409－4 412.

［3］ 劉樹德，孫建山，謝元靜.一類奇攝動擬線性邊值問題的激波解［J］.數學物理學報，2012，32（2）：312－319.

［4］ Holmes M H.Introduction to Perturbation Meyhods［M］.New York：Springer－Verlag，1999.

［5］ Nayfeh A H.Introduction for Perturbation Techniques［M］.New York：John Wiley ＆ Sons，1981.