試談求函數值域的基本思想及方法

孔曉紅

（甘肅省永靖縣永靖中學，甘肅 永靖 731600）

試談求函數值域的基本思想及方法

孔曉紅

（甘肅省永靖縣永靖中學，甘肅 永靖 731600）

本文簡述了求函數值域（或最值）常用的基本方法函數的值域是研究函數不可缺少的一個重要方面。求函數值域是函數這部分內容的重、難點問題之一。求函數值域首先要考察定義域。以一次函數、二次函數、反比例函數、指數函數、對數函數、冪函數、三角函數等基本函數的圖象和性質為基礎，尤其要熟練掌握二次函數式在給定區間上值域的求法。應用化歸思想、方程思想、相互制約思想、幾何思想、基本不等式以及單調性、奇偶性、周期性等函數性質。

函數；值域；教學方法

一、求二次函數式在自然定義域上的值域，一般將函數式y=ax2+bx+c（a≠0）化為y=a（x-m）2+n的形式，這里化成這種形式體現兩個優點：①知道圖象的頂點坐標（m，n）、對稱軸及函數最值；②函數的兩個單調區間為（-∞，m]、[m，+∞）。這樣，若a＞0，其值域為[m，+∞）；若a＜0，其值域為（-∞，m]

求二次函數式在限定區間D上的值域，先考察頂點橫坐標m與區間D的關系。如果m∈D，那么一個最值就是n，再通過考察區間D的兩個端點對應的函數值就能確定值域；如果m?D，那么D必是函數的單調區間，利用單調性就能求出值域。

二、化歸思想——通過替換或變形等方法把函數轉化為基本函數式或基本函數有聯系的形式，進而利用基本函數的圖象和性質確定出值域

因此，可通過替換化歸為冪函數后就可求出值域。

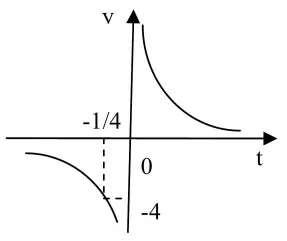
如圖可知y≤-4或y＞0，∴函數的值域為（-∞，-4]∪（0，+∞）。

三、方程思想——一個函數式實際上就是關于自變量x與函數值y的方程，而根據函數的定義可知，這個方程必關于x有解，因此有時我們把函數式變形為關于x的方程后，利用方程有解的條件建立關于y的不等式關系，從而求出值域

【例3】：求函數y=log2ax+2logax+2的值域。

分析：把函數式視為關于x的方程，則這個方程關于x有解，因為x∈（0，+∞），所以logax∈R，這樣把函數式看作關于logax的一元二次方程，那么這個方程恒有解，利用一元二次方程有解的條件就能求出值域。

解：因x＞0，∴logax∈R，設logax=t，則函數式可變形為t2+2t+（2-y）=0 由Δ=4-4（2-y）≥0解得y≥1，故函數的值域是[1，+∞）。

四、制約思想——自變量x與函數值y相互依存又相互制約。

分析：由于y受sinx的制約，而sinx∈（-1，1），因此從函數式解出sinx=f（y），通過-1≤f（y）≤1可求得值域。

分析：由于y受x2的制約，而x2≥0，因此從函數式解出x2=f（y），通過f（y）≥0能確定值域。

五、幾何思想——幾何思想即數形結合思想，通過作出函數的圖象或根據函數式所表示的意義畫出相應圖形，進而求出值域

思路一：畫出函數的圖象，可觀察出值域。思路二：由于|x-3|-|x+1|表示數軸上的點到3的距離與到-1的距離之差，因此，通過數軸可知值域是[-4，4]。

六、注意留意基本不等式即函數的單調性

【例7】：求函數y=x（3-2x），0＜x＜1的值域。

除以上基本思想方法外，要注意考察奇偶性與周期性。如果是奇函數或偶函數，我們只求正區間或負區間上函數值的范圍，根據對稱性就能確定值域；如果是周期函數，只求一周期區間上的值域。

總之，求值域是個較困難且較為靈活的問題，需靈活運用所學，靈活解決。

[1]史海平.一類函數值域的新求法[J].數學教學通訊，1989（05）.

[2]方亞娜.函數值域的求法[J].甘肅教育，1998（11）.

[3]李建標.關于函數值域的概念及其應用[J].中學教研（數學），2005（03）.

G623

A

1674-9324（2014）22-0100-02

孔曉紅（1980—），女，甘肅永靖，現任中學一級教師。