三分謝爾賓斯基墊片上的標準拉普拉斯算子

王 麗

(湖州職業技術學院，浙江 湖州 313000)

0 引言

首先回顧一下三分謝爾賓斯基墊片(SG3)。把一個正三角形看作K0(包括三個頂點p1，p2，p3)，三等分三條邊可得到九個小正三角形，去掉中間三個。這樣重復做下去，最后得到的“極限集”就是三分謝爾賓斯基墊片。

分形集可以通過構造迭代函數系[1]而得到。SG3就可以用由六個部分組成的迭代函數系得到，每一部分都和整體相似，壓縮比為這六個相似壓縮映射如下

這里x，y∈R。如圖1。用K來表示SG3，K就是自相似集[2]，那么

下面是本文中的一些符號:

①Vm是m－層上所有頂點的集合，m≥0;

②LA(V0)[2]是V0上所有拉普拉斯算子的集合;

③[Hm+1]Vm是指 Hm+1在 Vm上的限制;

④DF(Vm)[2]是Vm上所有狄利克雷型的集合;

⑤l(Vm)={f:Vm→R}，m≥0;

⑥Гm={Vm，Em}，這里Em是m－層上所有的邊的集合，m≥0;

⑦x～ym意思是:x和y是在一個m－單元的兩個點，它們由一條邊連接在一起，m≥0;

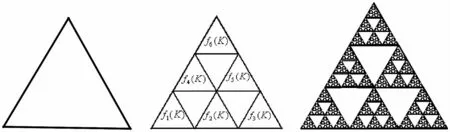
圖1 K0，K1和 SG3

1 三分謝爾賓斯基墊片的調和結構

在這一部分中，我們構造一個{Vm}m≥0上的r－網“自相似”相容序列((Vm，Hm)[2]。用如下方陣來定義三分謝爾賓斯基墊片上最初的拉普拉斯算子D，D∈LA(V0)，V0={p1，p2，p3}。

對任意初始D∈LA(V0)，我們都能找到一個自相似拉普拉斯算子序列Hm∈LA(Vm)，定義如下:

定義1[2](相容序列):設 Vm是一有限集，且對任意 m≥0有 Hm∈LA(Vm)。(Vm，Hm)≤(Vm+1，Hm+1)當且僅當Vm?Vm+1和[Hm+1]Vm=Hm成立，那么對所有 m≥0 有(Vm，Hm)≤(Vm+1，Hm+1)，這時{(Vm，Hm)}m≥0稱為一個相容序列。

定義2[2](調和結構):當且僅當{(Vm，Hm)}m≥0是 r－ 網的一個相容序列時是一個調和結構。而且，當對所有i∈S有0＜ri＜1時，調和結構)稱為是正則的。

性質1:若D∈LA(V0)，且，對所有 i∈S 有 ri＞0，由下式來定義ε(m)∈DF(Vm)。

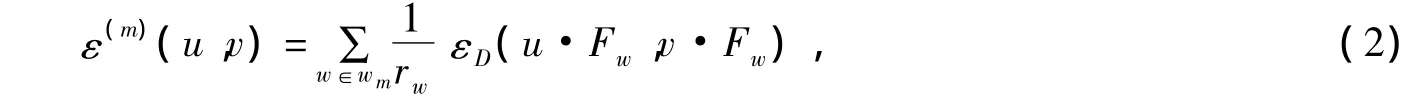
這里 u，v∈l(Vm)，w=w1w2…wm∈Wm，有 rw=rw1…rwm，且 εD= ε0，還有 Hm∈LA(Vm)。記 ε(m)= εHm。

定義εm= ε(m)，這里 εm是圖能[4]。

而且 ε(m+1)(u，v)

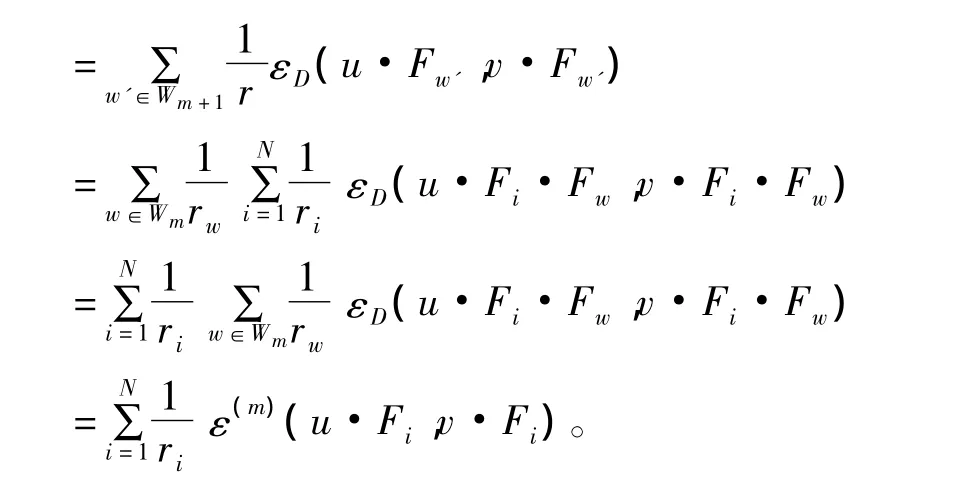
因此，有

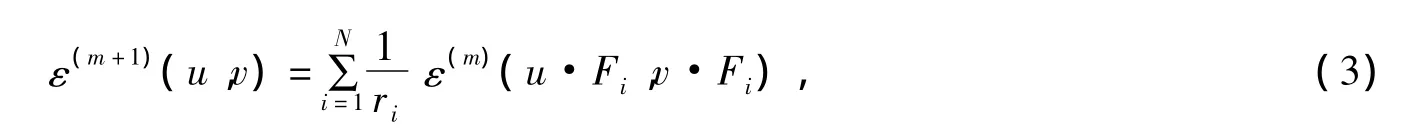
這里u，v∈l(Vm)，我們讓ε是圖能εm的極限。

定理1:對w∈Wm，由Rwf=f·Fw來定義Rw:l(Vm)→l(V0)。那么對所有m≥0，有

證明:注意到 εHm(u，v)是一個內積，因此由內積定義有 εHm(u，v)= －uTHmv，又由(1)ε(m)(u，v)