滑模控制在變載荷高性能系統中的應用

王金鵬，吳向東，張兵，陸世榮，李波

(西南交通大學機械工程學院，成都 610031)

滑模控制在變載荷高性能系統中的應用

王金鵬，吳向東，張兵，陸世榮，李波

(西南交通大學機械工程學院，成都 610031)

為比較傳統的PID控制與滑模控制(SMC)在非線性變化的變載荷負載條件下在控制性能方面的差異，通過搭建PID與SMC控制器模型、永磁同步電機(PMSM)控制模型以及運動機構及負載模型，構建了整個控制測試平臺。在此平臺下使用Matlab與ADAMS軟件聯合仿真，對2種算法的控制性能進行分析。經比較發現:滑模控制較PID控制在控制精度、調節時間、魯棒性及能量控制等方面均具有一定的優越性。

滑模控制;PID控制;變載荷;性能仿真

機電控制系統中，變載荷負載的運動特性主要表現在外部負載的運動突變、運動模型轉動慣量的突變以及機械諧振等方面。在機電控制系統的整個運動控制過程中，由于變載荷負載的狀態及整個運動系統轉動慣量存在較大變化，故模型很難準確、全面地反映整個運動控制過程中運動對象的運動特性［1］。同時，變載荷負載的非線性變化特性加強了整個機電控制系統的非線性，使得變載荷情況下高性能控制更加復雜，控制難度更高。

傳統PID控制存在積分飽和與微分突變現象，這一缺陷使得在對變載荷負載進行控制時，對是否能夠達到較高控制性能提出了疑問。滑模控制(SMC)作為一種先進的控制理論，經過多年發展已形成一個相對獨立的研究分支，是目前自動控制系統領域一種常見的設計方法［2］。在滑模控制中，滑動模態可進行設計且與對象參數及擾動無關，所以滑模控制使系統在受到參數攝動和外部干擾時具有不變性。同時，滑模控制還具有響應快速、無需系統在線識別、物理實現簡單等優點［3-4］。這些特性使得滑模控制在非線性系統及伺服系統方面得到廣泛應用。

本文以所設計的變載荷運動控制系統為控制對象，通過引入滑模控制，與傳統的PID控制進行比較，分析其在控制精度、調節時間、魯棒性、能量控制等方面的特點，驗證滑模控制在變載荷高性能系統中的可行性。

1 滑模變結構控制基本原理

滑模變結構控制的基本原理為:根據系統所需控制性能，在系統狀態空間中設計出開關面(狀態空間不連續曲面)，通過滑模控制器使系統狀態向量從開關面之外向開關面收束。當系統狀態向量到達開關面后，反饋控制的作用將發生變化，使系統性能達到期望指標。

滑模變結構控制與常規控制的根本區別為其在變控制率和系統結構在滑模面上的不連續性，即隨時間變化的開關特性。該特性使控制系統在一定特性下沿規定的狀態軌跡做小幅度、高頻率的上下運動。由于滑動模態是預先設計的，系統對于參數變化及外部擾動不敏感，因此處于滑模運動的系統具有很強的魯棒性。

2 變載荷系統模型介紹

2.1 整體模型搭建

在搭建運動機構與負載的物理模型時，采用西南交通大學李波的設計模型［1］。該模型的設計思路為:使用工程軟件(SOLIDWORK、ADAMS)，依據工程參數創建出所需模型，并在軟件中對模型進行參數設置，使其盡量貼近實際工程運動情況。

該模型采用的裝置主要包括交流伺服電機及伺服電機控制器、減速器、負載固定盤、負載、編碼器等，如圖1所示。所涉及的各種運動機構的質量及轉動慣量如表1所示。

圖1 變載荷控制系統模型

表1 各機構參數

2.2 ADAMS軟件下的變載荷模型

2.2.1 變載荷仿真物理模型

因模型支撐架部分對仿真結果沒有影響，故在ADAMS軟件中仿真時對整個模型進行簡化處理，只載入運動機構及負載部分以便于仿真。模型的各項參數設置與實物參數基本相同，其變載荷模型如圖2所示。

圖2 變載荷模型

2.2.2 變載荷模型控制參數

在變載荷運動控制系統中，主要對負載運動位置角度實現精確控制。在ADAMS軟件中，變載荷負載主要表現為在給定時刻改變負載的質量及其轉動慣量。整個變載荷運動控制系統的運動規律為:交流伺服電機帶動負載固定盤和6個負載轉動，固定盤每隔一段時間拋出一個負載，拋出后繼續旋轉直至將6個負載全部拋出。控制模型中負載的轉動慣量變化趨勢如圖3所示，對負載旋轉位置的角度位置要求如圖4所示。

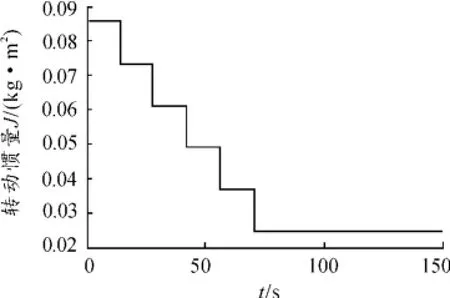
圖3 負載轉動慣量

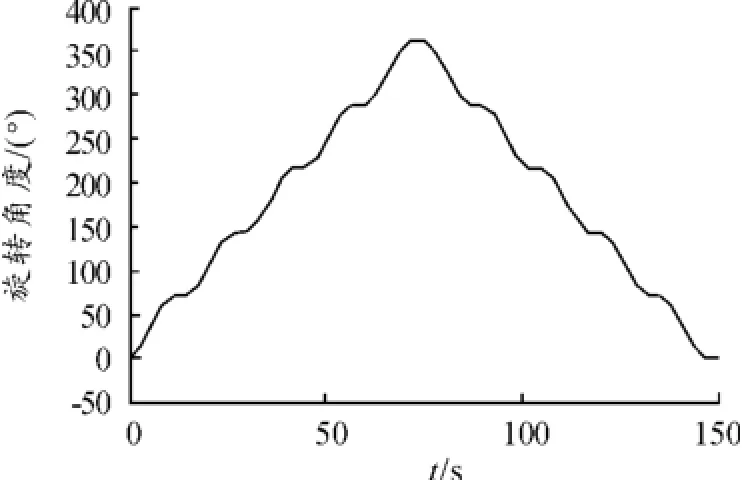
圖4 負載旋轉角度

2.3 交流伺服電機模型

交流伺服電機控制模型通過Matlab下的SIMULINK模塊搭建。因ADAMS模型采用力矩輸入，故交流伺服電機模型采用力矩輸出控制。

根據電機學理論可得，電機轉速與轉矩間的傳遞函數為

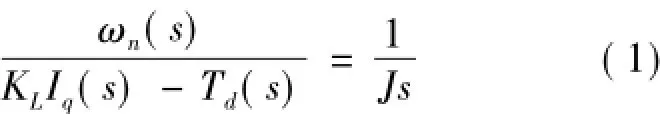
式(1)中:ωn為電機轉子機械角頻率;Td為負載轉矩。

加入速度和電流各環調節器的傳遞函數模塊后，可在Matlab軟件中構建出永磁同步電機調速系統的動態結構圖，如圖5所示。其中，βi為電流反饋系數，αn為速度反饋系數［6］。在Matlab中搭建的伺服電機運動模型如圖6所示。

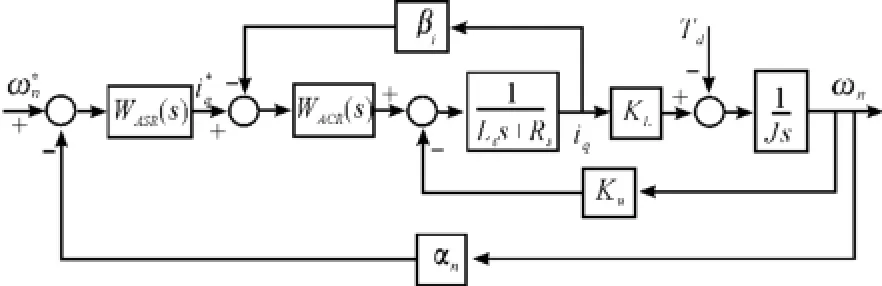
圖5 永磁同步電機調速系統動態結構

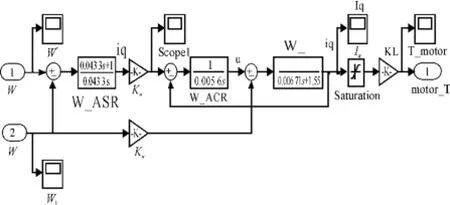
圖6 伺服電機運動模型

2.4 滑模變結構位置環調節器設計

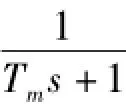
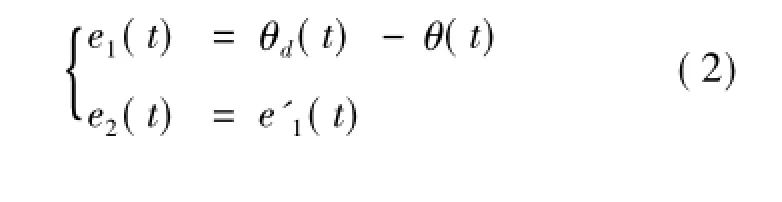
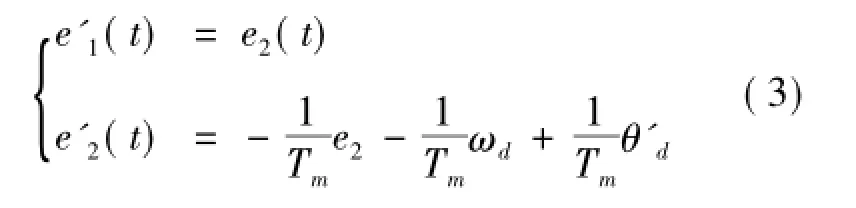
式(2)、(3)中:θd(t)為給定角度信號;θ(t)為角度反饋信號。設計位置環滑模函數為

其中，c滿足Hurwitz條件，即c＞0。滑模變結構調節器輸出為

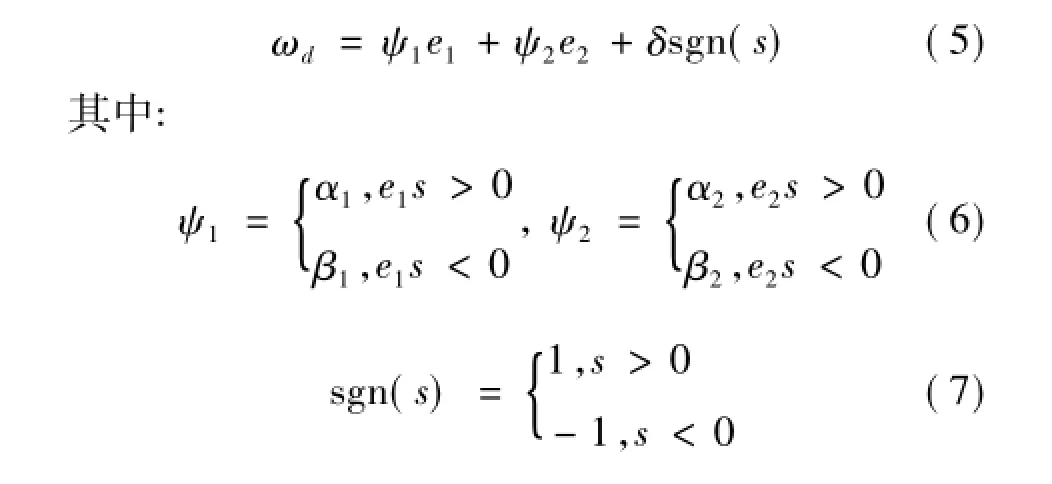
位置環滑模變結構調節器結構如圖7所示［8］，Matlab中搭建的滑模控制模型如圖8所示。

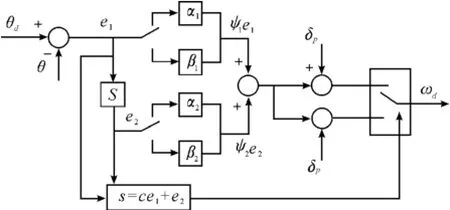
圖7 位置環滑模變結構調節器結構

圖8 滑模控制模型

3 SMC與PID控制性能比較

將ADAMS軟件下的運動機構與負載模型集成到Matlab軟件中。設置好各項參數后，通過與Matlab進行聯合仿真來對SMC性能與傳統的PID控制性能進行比較。

考慮到電機實際工作情況，需對電機的瞬時最大電流、轉速及輸出轉矩進行限幅設置(瞬時最大電流為7.8A，最高轉速為5 000 r/min，最大輸出轉矩為3.82 N·m)。同時為保證仿真結果具有可比性，在模型中加入能量檢測單元。集成后的PID控制模型與滑模控制模型分別如圖9、10所示。

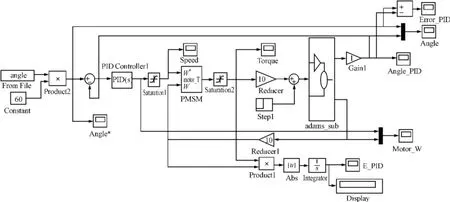
圖9 PID控制模型

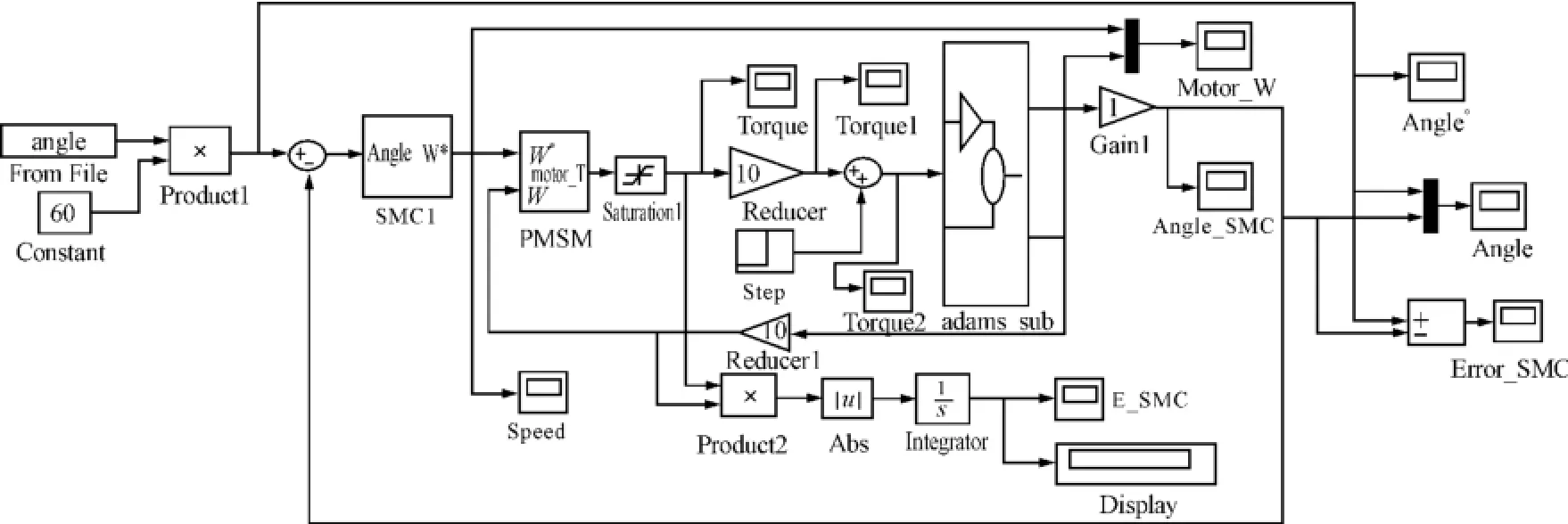
圖10 滑模控制系統模型

對于傳統PID控制與滑模控制主要通過以下幾個方面進行比較。

3.1 PID與SMC固定負載條件下對階躍輸入的響應

將負載模型調整為固定載荷，驗證PID與SMC在階躍輸入下的反應情況。對模型輸入幅值為60的階躍信號后，5 s時間內能量輸出均為100 J時，PID與SMC兩種模型的角度響應曲線與位置誤差曲線分別如圖11、12所示。

從圖11、12可看出:在輸出能量相同的情況下，兩者均能實現對角度的較好跟隨。但對誤差曲線放大后可看出:PID控制誤差在-0.025°～-0.02°，而SMC誤差在±0.005°以內，說明在高精度控制條件下，SMC在控制精度方面表現更優。

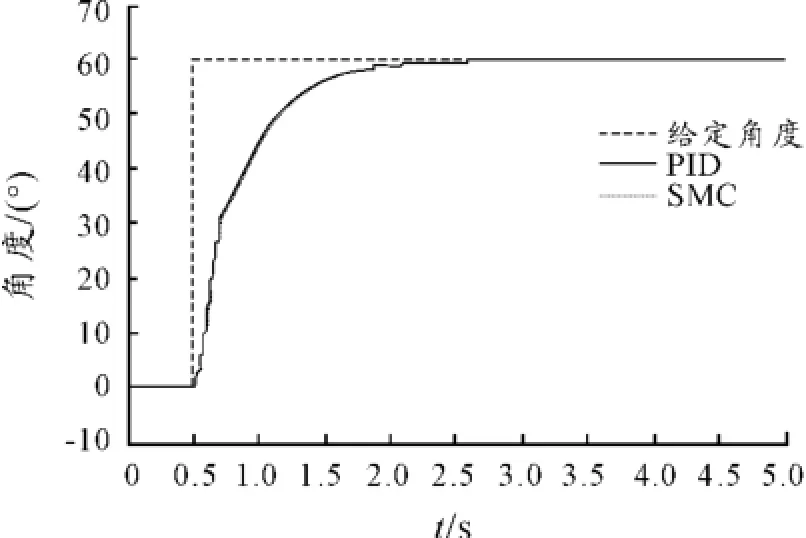
圖11 PID/SMC定載荷角度曲線

3.2 PID與SMC變載荷負載條件下的響應

為驗證PID與滑模變結構兩種控制算法對不同負載情況的適應性，兩種模型均選用與固定負載條件下相同的參數。仿真結果如圖13、14所示。

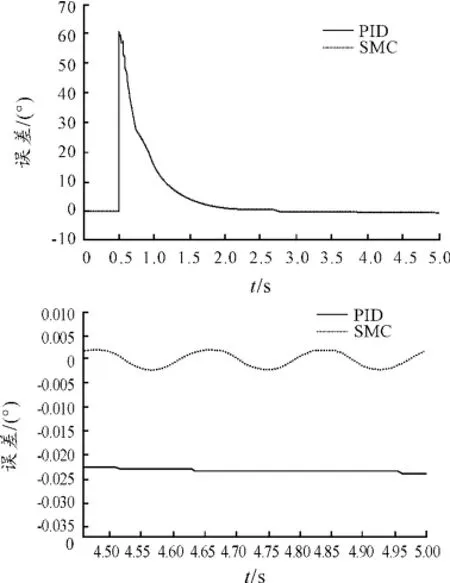
圖12 PID/SMC定載荷位置誤差曲線

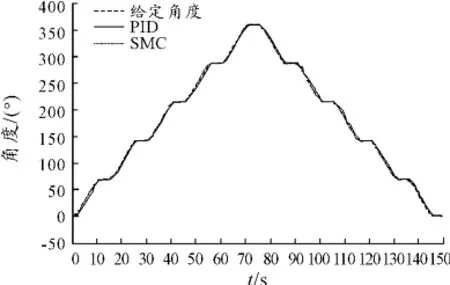
圖13 PID/SMC變載荷角度曲線

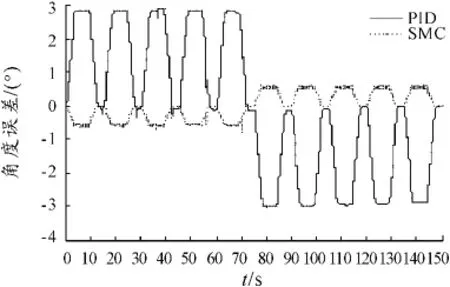
圖14 PID/SMC變載荷角度誤差曲線

從圖13、14可看出:PID與SMC在變載荷負載條件下均能夠對目標曲線進行較好跟隨。但通過誤差曲線可發現:PID控制誤差范圍在±3°以內，而SMC誤差范圍在±0.6°以內。能量方面，PID控制下系統總輸出能量為805.8 J，SMC控制下系統總輸出能量為798.4 J，PID能量輸出稍大。

3.3 PID與SMC變載荷負載加入突變轉矩下的響應

為檢測PID與SMC的抗干擾能力，在時間為80 s時加入35.5 N·m的階躍轉矩信號，對仿真結果進行分析。仿真結果如圖15、16所示。

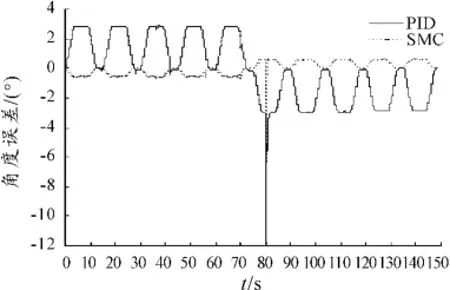
圖15 突變轉矩下PID/SMC變載荷角度誤差曲線

由圖16、17可看出:當加入階躍轉矩后，PID與SMC在角度誤差上均有較大變化。其中PID角度最大誤差為11.9°，SMC角度最大誤差為6.4°。PID恢復到正常誤差范圍的時間為2 s，SMC恢復到正常誤差范圍的時間為0.6 s。從能量曲線上看，在未加入階躍轉矩前，兩控制算法對能量的使用情況非常接近;加入階躍轉矩后PID控制的能量輸出相比SMC控制有增加。在能量輸出方面，PID為1.325×104J，SMD能量輸出為1.316× 104J。

當對系統加大干擾力矩(增加為40 N·m)時，SMC隨瞬時誤差較大，但仍能夠保持對系統的控制，而PID控制已經失穩，如圖17、18所示。

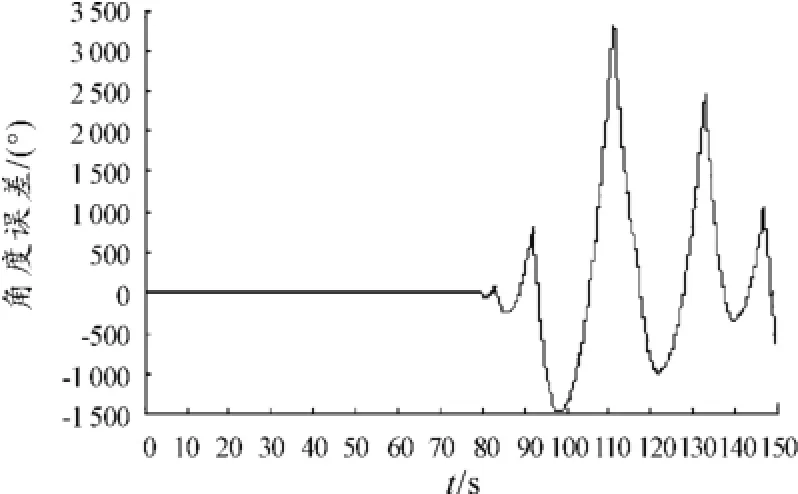
圖17 PID變載荷角度誤差曲線

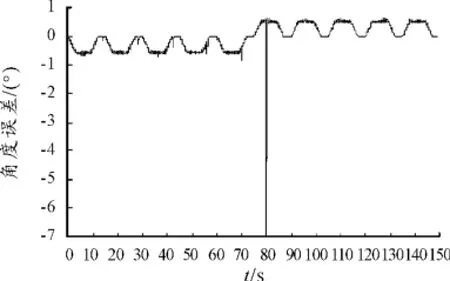
圖18 SMC變載荷角度誤差曲線

4 結束語

1)在變載荷運動控制系統的高精度控制要求下，SMC在位置控制方面相比傳統PID控制精度更高。

2)當角度誤差較大時，SMC相對傳統PID控制將誤差調整到常規狀態的調節時間更短。

3)當負載變化較為復雜時，SMC相比傳統PID控制的魯棒性更強。

4)當負載變化較為平穩時，傳統PID控制與SMC在能量輸出方面性能比較接近。但當負載變化較快時，SMC在能量控制方面較傳統PID更為節約。

綜上所述，滑模控制的開關特性使其能在不同控制結構間進行切換，負載變化較大時依然能夠獲得較好的控制性能。PID控制則由于積分飽和、微分突變現象導致其控制性能受到一定限制。因此，在對變載荷負載進行高性能控制時，滑模控制相比傳統PID控制在控制精度、調節時間、魯棒性及能量控制方面更具有優越性。但由于時間滯后、空間滯后及系統慣性的影響，滑模控制會產生一定的高頻抖振，在應用時應引起注意。

［1］李波.PDF策略在變載荷高性能控制系統中的設計及仿真［J］.工程設計學報，2013(1):49-54.

［2］張曉宇，蘇宏.滑模控制理論進展綜述［J］.化工自動化及儀表，2006，33(2):1-8.

［3］劉金琨，孫富春.滑模控制理論及其算法研究與進展［J］.控制理論與應用，2007，24(3):407-418.

［4］劉金琨.滑模控制Matlab仿真［M］.北京:清華大學出版社，2005.

［5］廖曉鐘，劉向東.控制系統分析與設計［M］.北京:清華大學出版社，2002.

［6］陳先鋒，舒志兵，趙英凱.基于PMSM伺服系統的數學模型及其性能分析［J］.機械與電子，2005(1):41-43.

［7］嚴彩忠，舒志兵.變加減速算法在位置伺服系統中的應用與分析［J］.機械制造，2007(1):15-16.

［8］陳先鋒.PMSM位置伺服系統的分析設計及其應用研究［D］.南京:南京工業大學，2005.

(責任編輯 楊黎麗)

Control System Design and Simulation in Variable Load High-
Performance System with Sliding Mode Control

WANG Jin-peng，WU Xiang-dong，ZHANG Bing，LU Shi-rong，LI Bo
(School of Mechanical Engineering，Southwest Jiaotong University，Chengdu 610031，China)

sliding mode control;PID control;variable load;performance simulation

:In order to compare the control performance differences between the traditional PID control and sliding mode control(SMC)in the non-linear changes variable load，a control test platform which includes PID/SMC controller model，permanent magnet synchronous motor(PMSM)motor control model，and a movement mechanism and load models were built.In this platform，through the software co-simulation of MATLAB and ADAMS，a detailed analysis on the performance of both was done which was based on the control performance of the two control algorithms.By comparison，the sliding mode control can be found better than traditional PID control in the control precision，adjustable time，robustness and energy control.

10.3969/j.issn.1674-8425(z).2014.06.010

2014-02-26.

中央高校基本科研業務費專項資金創新項目(SWJTU11CX024)

王金鵬(1988—)，男，碩士研究生，主要從事機電液一體化及控制系統建模仿真研究。

王金鵬，吳向東，張兵，等.滑模控制在變載荷高性能系統中的應用［J］.重慶理工大學學報:自然科學版，2014(6):53-59.

format:WANG Jin-peng，WU Xiang-dong，ZHANG Bing，et al.Control System Design and Simulation in Variable Load High-Performance System with Sliding Mode Control［J］.Journal of Chongqing University of Technology:Natural Science，2014(6):53-59.

TH122

A

1674-8425(2014)06-0053-07