LINEX損失函數(shù)下具有時間變化效應(yīng)的信度模型

李新鵬，努爾古麗·艾力，吳黎軍

(1.新疆農(nóng)業(yè)大學(xué)數(shù)理學(xué)院，烏魯木齊 830052; 2.新疆大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院，烏魯木齊 830046)

LINEX損失函數(shù)下具有時間變化效應(yīng)的信度模型

李新鵬1，努爾古麗·艾力1，吳黎軍2

(1.新疆農(nóng)業(yè)大學(xué)數(shù)理學(xué)院，烏魯木齊 830052; 2.新疆大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院，烏魯木齊 830046)

在經(jīng)典信度理論中，運(yùn)用平方損失函數(shù)來估計保費(fèi)會導(dǎo)致很高的懲罰額，影響保險市場的競爭力，同時在實(shí)際應(yīng)用中，索賠額間是風(fēng)險相依的。在LINEX損失函數(shù)下考慮了各年索賠額間具有此種風(fēng)險相依結(jié)構(gòu)的信度理論，得到了Bühlmann和Bühlmann-Straub模型的信度保費(fèi)。

信度模型;LINEX損失函數(shù);時間變化效應(yīng)

在保險的實(shí)際應(yīng)用中，精算師的一項(xiàng)重要任務(wù)就是為給定的風(fēng)險制定一個合適的保費(fèi)。而信度理論是精算學(xué)中最重要的保費(fèi)厘定技術(shù)。現(xiàn)代信度理論起源于Bühlmann［1］。他闡釋了任意分布下的凈保費(fèi)信度估計，認(rèn)為信度理論是基于過去的索賠經(jīng)歷來制定保費(fèi)的一種定量方法。信度保費(fèi)為樣本均值和聚合保費(fèi)的加權(quán)和，其中權(quán)重因子又被稱為信度因子。

令Xj表示保單持有人在第j個保單時期的索賠額，Xj的分布依賴于風(fēng)險參數(shù)Θ。由于風(fēng)險的非齊次性，一般假設(shè)Θ是隨機(jī)變量，具有先驗(yàn)分布為f(θ)。若給定Θ=θ，Xj，j=1，2…，n獨(dú)立同分布，分布函數(shù)為F(x，θ)。信度理論的目的是在給定保單持有人的前n個時期索賠額來計算第(n+ 1)個時期的保費(fèi)。如果將估計限定在索賠額的線性函數(shù)中，則得到著名的信度公式

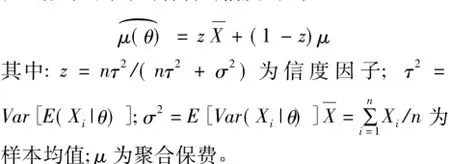
經(jīng)典的信度理論中，假定不同年份的索賠額有共同的風(fēng)險參數(shù)，在風(fēng)險參數(shù)給定的條件下，各年的索賠相互獨(dú)立且具有相同的分布。然而，在實(shí)際應(yīng)用中，各年索賠額之間是風(fēng)險相依的，不同年份的索賠額間具有時間變化效應(yīng)。2012年，溫利民等［2］在平方損失函數(shù)下研究了各年索賠風(fēng)險間具有時間變化效應(yīng)的信度模型，得到了相應(yīng)的信度保費(fèi)。考慮時間方面相依性的信度模型與實(shí)際情況更為符合，Bolancé等［3］在2003年建立了索賠頻率風(fēng)險模型，得到了時間效應(yīng)為自相關(guān)時間序列時的信度保費(fèi)。Frees等［4］在2005年研究了時間效應(yīng)為Student-t copula下的信度保費(fèi)。

經(jīng)典信度理論中，總是用對稱損失函數(shù)來估計保費(fèi)，如平方損失函數(shù)等。但使用平方損失函數(shù)會導(dǎo)致很高的懲罰額，尤其對小額風(fēng)險事故的投保人，這勢必會影響保險市場的競爭力，不被客戶接受。針對這一問題，20世紀(jì)70年代許多學(xué)者注意到由過高估計或過低估計引起的損失并不相同，且在某些情況下，使用對稱損失函數(shù)所估計的保費(fèi)不準(zhǔn)確。這一點(diǎn)在許多文章中都給出了實(shí)例，如Berger［5］、Varian［6］。于是引入了非對稱損失函數(shù)。

非對稱損失函數(shù)能夠更好地衡量風(fēng)險，更公平地制定保費(fèi)。

Varian［6］于1975年提出了一個非對稱損失函數(shù)，被稱為LINEX損失函數(shù)，如式(1)所示:

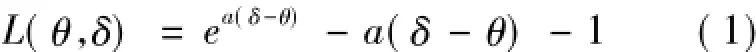
其中:a＞0為一常數(shù);θ為真實(shí)值;δ為θ的估計值。它引起了許多研究人員的重視:Zellner［7］于1986年將該函數(shù)用于預(yù)測問題的Bayes分析;Parsian［8］將其用于多維正態(tài)分布的廣義Bayes估計;溫利民等［9］在2012年將其用于信度保費(fèi)估計。使用LINEX損失函數(shù)估計保費(fèi)，不會因?yàn)橥侗Ｈ擞袔状未箢~理賠就索取高額保費(fèi)，因此，用LINEX損失函數(shù)估計的保費(fèi)更公平、更合理。

本文在LINEX損失函數(shù)下考慮了具有時間變化效應(yīng)的信度模型，并且得到了相應(yīng)的信度保費(fèi)。本文安排如下:第2部分介紹了模型假設(shè)與準(zhǔn)備知識;第3部分為LINEX損失函數(shù)下具有時間變化效應(yīng)的Bühlmann-Straub模型的信度估計;第四部分為文章的結(jié)論。

1 模型假設(shè)與準(zhǔn)備

在經(jīng)典信度理論中，假設(shè)保單組合的風(fēng)險參數(shù)為Θ，且有n年的索賠額，由于風(fēng)險的非齊次性，風(fēng)險參數(shù)Θ假定為隨機(jī)變量。但與經(jīng)典的信度理論不同，本文假設(shè)索賠隨機(jī)變量X1，X2，…，Xn有各自的風(fēng)險參數(shù)Θ1，Θ2，…，Θn，且這些風(fēng)險參數(shù)具有某種相依結(jié)構(gòu)。模型的基本假設(shè)如下:

2 LINEX損失函數(shù)下的信度保費(fèi)估計

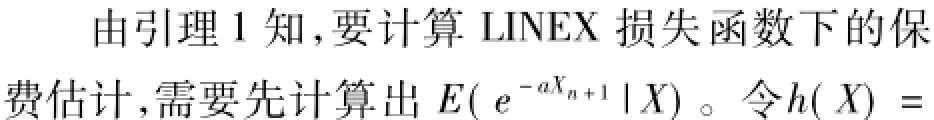
3 結(jié)束語

本文在LINEX損失函數(shù)下研究了具有時間變化效應(yīng)的Bühlmann-Straub信度模型，并推導(dǎo)出其信度估計。對于參數(shù)a，τi，σ2i，i=1，2，…，n+1的估計是下一步研究的方向。

［1］Bühlmann H，Gisler A.A course in credibility theory and its applications［M］.Netherlands:Springer，2005:77 -264.

［2］溫利民，鄭丹，章溢.具有時間變化效應(yīng)的信度模型［J］.江西師范大學(xué)學(xué)報:自然科學(xué)版，2012，36(3): 249-252.

［3］Bolancé C，Guillé M，Pinquet J.Time-varying credibility for frequency risk models:estimation and tests for autoregressive specification on the random effects［J］.Insurance:Mathematics and Economics，2003，33(2):273 -282.

［4］Frees E W，Wang Ping.Credibility using copulas［J］. North American Acturial Journal，2005，9(2):31-48.

［5］Berger J O.Statistical Decision Theory:Foundations，Concepts and Methods［M］.New York:Academic Press，1980.

［6］Varian H R.A Bayesian approach to real estimate assessment，Studies in Bayesian Econometrics and Statistics in Honor of Leonard J Savage［J］.Amsterdam:North Holland，1975，195-208.

［7］Zellner A.Bayesian estimation and predictionusing asymmetric loss functions［J］.Jamer Statist Assoc，1986，81:446-451.

［8］Parsian A.On the admissibility of all estimator of a normal mean vector under a LINEX loss function［J］.Ann Inst statist Math，1990，42:657-669.

［9］Wen Limin，Zhang Xiankun，Zheng Dan，et al.The credibility models under LINEX loss function［J］.Chin. Quart.J.of Math，2012，27(3):397-402.

［10］李新鵬，吳黎軍.平衡損失函數(shù)下具有時間變化效應(yīng)的信度保費(fèi)［J］.重慶理工大學(xué)學(xué)報:自然科學(xué)版，2013，27(4):133-137.

(責(zé)任編輯 何杰玲)

Credibility Models with Time Varying Effects
under LINEX Loss Function

LI Xin-peng1，Nurgul Eli1，WU Li-jun2

(1.College of Mathematics and Physics，Xinjiang Agriculture University，Urumqi 830052，China; 2.College of Mathematics and System Sciences，Xinjiang University，Urumqi 830046，China)

In classical credibility theory，the actuary uses squared-error loss function to estimate premium，but it can lead to very high penalties which affects competitive strength of insurance market. On the other hand，classical credibility theory assumes that the claim amounts of one insurance policy are independent.However，in practical applications，the claim amounts are risks dependent.Wen et al studied the credibility model with dependence structure called time changeable effects and obtained credibility premium in 2012.Moreover，credibility premium using LINEX loss function can be equitable.So this paper considered the credibility model with time varying effects among claim amounts and obtained Bühlmann and Bühlmann-Straub models’credibility premiums.

credibility model;LINEX loss function;time varying effects

O212

A

1674-8425(2014)06-0135-04

10.3969/j.issn.1674-8425(z).2014.06.027

2014-02-28

國家自然科學(xué)基金資助項(xiàng)目(11361058)

李新鵬(1986—)，男，甘肅人，碩士，主要從事精算數(shù)學(xué)研究。

李新鵬，努爾古麗·艾力，吳黎軍.LINEX損失函數(shù)下具有時間變化效應(yīng)的信度模型［J］.重慶理工大學(xué)學(xué)報:自然科學(xué)版，2014(6):135-138.

format:LI Xin-peng，Nurgul Eli，WU Li-jun.Credibility Models with Time Varying Effects under LINEX Loss Function［J］.Journal of Chongqing University of Technology:Natural Science，2014(6):135-138.