彈簧串并聯特點及應用*

陳玉軍 董芳芳

(鹽城景山中學 江蘇 鹽城 224002)

在我們的日常生活中，彈簧的形態各異，處處都在為我們服務，而彈簧問題又在高考物理中扮演著很重要的角色，小小的彈簧，涉及到對靜力學問題、動力學問題、動量守恒和能量守恒問題、振動問題、功能關系問題等知識點的理解，可以考查學生對于一些重要思維方法和解題思想的運用能力．

在實際生活中，彈簧是可以串聯或并聯使用的，譬如健身用的拉力器，多根彈簧就屬于彈簧的并聯．對于彈簧的串聯，從等效的角度來說，任何一個大彈簧都可以看成是由多個小彈簧串聯而成的．新課程標準的三維目標要求教師在傳授基本知識的同時，要培養學生自主學習、探索創新的能力．彈簧串并聯的連接方式和電阻串并聯的連接方式很相似，學生在初中物理中已經熟知電路的串并聯原理，在此基礎上可以帶領學生研究：彈簧在進行串聯和并聯以后，其特點會發生什么變化，再做適當的大學知識拓展，激發他們的學習和研究問題的興趣，面對彈簧串并聯的具體情況進行分析．

為了簡單起見，下面以兩根彈簧為例，對實際問題的應用進行分析．

1 彈簧的串聯問題

如圖1所示將兩根勁度系數分別為κ1和κ2的輕彈簧串聯在一起，在外力F的作用下兩根彈簧都被拉伸.在不考慮彈簧本身重量的前提下，每根彈簧所受的彈力皆為F，設兩根彈簧的伸長量分別為Δx1和Δx2，由胡克定律

F=κ1Δx1=κ2Δx2

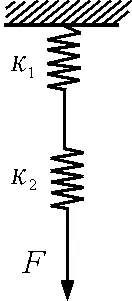
圖1

兩彈簧串聯后看作一根彈簧，等效勁度系數設為κ，則對于整個系統來說，總的伸長量為

則

如果串聯的彈簧組下面掛個質量為m的小球，彈簧和小球就構成一個彈簧振子系統，若不計彈簧質量，系統的圓頻率為

其中κ為彈簧的勁度系數，m為彈簧振子的質量．于是系統的圓頻率

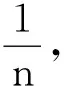
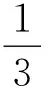
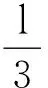
所以彈簧剪斷后，勁度系數變大，彈簧變硬．

應用2:如圖2所示，在光滑的水平面上，有一個質量為m的物塊由勁度系數分別為κ1和κ2，原長都為l輕彈簧連接著，現用一水平力F向左壓彈簧2，求彈簧2的右端點A移動的距離是多少？

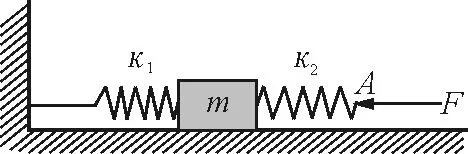
圖2

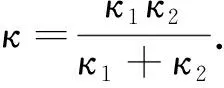
所以彈簧2的右端點A移動的長度是

拓展1:如果將圖2按圖3連接彈簧，彈簧2的右端點A移動的距離是多少？

圖3

解析：拓展1和原題中兩彈簧上的力都相等，符合彈簧串聯的特點，所以都可以按串聯規律解題，結果一樣．如果將物體拉離平衡位置其振動圓頻率為

但注意物體移動的距離不同．

拓展2:如果將圖2按圖4連接彈簧，在光滑的水平面上，質量為m的物塊由勁度系數分別為κ1和κ2，原長都為l輕彈簧連接著，彈簧另外一端和墻壁相連，靜止時彈簧都處于原長，此彈簧振子系統的圓頻率是多少？

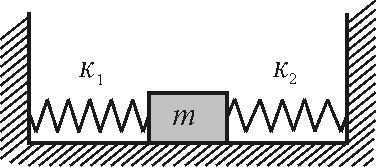
圖4

解析：圖4中兩彈簧的連接看似串聯，但在物體振動過程中兩彈簧的形變量大小相同，而彈力不等，不符合彈簧串聯的特點，因此此系統的圓頻率不能按串聯規律求解．(本題在后面解答)

應用3:如圖5(a)所示，已知物塊A和B的質量均為m，兩輕質彈簧勁度系數分別為κ1和κ2，已知兩彈簧原長分別為l1和l2，若不計兩物體的厚度，求現在圖中兩彈簧的總長度．

圖5

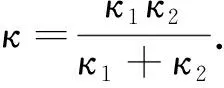
顯然這種解題方法是按照圖5(b)連接方式理解的．然而仔細分析題目，會發現上面輕質彈簧受力為mg，下面輕質彈簧的受力為2mg，所以不符合彈簧串聯的條件，因此不能按串聯特點進行計算．設上面彈簧壓縮量為Δx1，下面彈簧的壓縮量為Δx2，由胡克定律易得

因此現在彈簧的總長度為

我們反思出解答錯誤的原因是：這道題彈簧只是形式上的串聯形式，有些學生不經分析就亂套彈簧的串聯公式．綜合應用1、應用2和應用3，我們可以總結出：彈簧串聯的特點是每根彈簧的彈力相等．

2 彈簧的并聯問題

如圖6所示，將兩根原長相等、勁度系數分別為κ1和κ2的輕彈簧并聯接在一起，在外力F的作用下，兩根彈簧的伸長量相同，設兩個彈簧的伸長量均為Δx，利用胡克定律，則

F1=κ1ΔxF2=κ2Δx

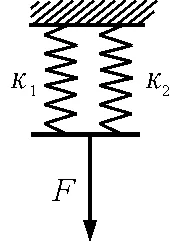
圖6

將兩彈簧并聯后看作一根彈簧，等效勁度系數設為κ，則彈簧系統受到的彈力大小應等于并聯的兩個彈簧的彈力之和，所以

F=κ1Δx+κ2Δx=(κ1+κ2)Δx

則對于整個系統來說κ=κ1+κ2

同理，彈簧振子的圓頻率為

可見，彈簧并聯構成的新彈簧的等效勁度系數等于并聯的每一個彈簧的勁度系數之和，如果n個相同的彈簧并聯，彈簧組的勁度系數是每個彈簧勁度系數的n倍．這個結論類似于串聯電路總電阻與各個電阻之間的關系．彈簧經并聯后勁度系數變大，彈簧系統變硬，圓頻率升高．火車車廂下的多個減震彈簧屬于并聯，如何并聯也關系到減震彈簧壽命以及它的一些性質．

在前面拓展2圖4連接的彈簧組中，在物體振動過程中兩彈簧形變量大小相同，物體所受的合力為兩彈簧彈力之和，符合兩彈簧并聯的特點，所以其振動的圓頻率應該為

應用4:一根輕質彈簧，其勁度系數為κ，下面掛重物為G的伸長量為l1，現在把該彈簧剪為相等的兩段再相并使用，下面仍掛重物為G，問這時新彈簧的伸長量l2為多少．

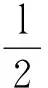
應用5:如圖7所示，a和b兩根輕質彈簧，它們的勁度系數分別為κa=1×103N/m，κb=2×103N/m，原長分別為la=6 cm，lb=4 cm， 在下端掛一重物G，物體受到的重力為10 N，求平衡時物體下降了多少[2]？

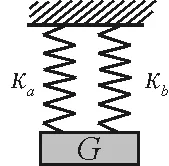
圖7

參考文獻[2]中給出的解答如下.

解析：由上面的推導知，a和b并聯后彈簧的勁度系數為

κ=(κa+κb)=3×103N/m

已知F=G，由胡克定律可得F=κΔx，把κ代入得Δx=3.3×10-3m．

然而仔細審題，會發現由于這兩根彈簧的原長和勁度系數不同，彈簧的形變量也不相同，所以根本不可以使用彈簧的并聯公式，再深究下去，由于平衡時兩根彈簧的的彈力不同，所以下面的重物必然會發生傾斜．出題者可能沒有真正領會到彈簧并聯的特點．如果把題目改成a和b兩根原長相等的輕質彈簧下掛一個可以看成質點的物體，那么以上分析過程就是合適的．

應用6:如圖8所示，兩個勁度系數分別為κ1和κ2的輕彈簧豎直懸掛，下端用光滑細繩連接，并有一光滑的輕滑輪放在細線上，滑輪下端掛一重為G的物體后滑輪下降，求滑輪靜止后重物下降的距離．

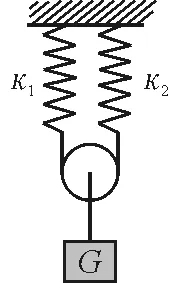
圖8

解析：兩個彈簧從形式上看似乎是并聯，故學生會由上面推導得到并聯后彈簧的勁度系數κ=κ1+κ2．設滑輪下降的距離為Δx,由胡克定律得κΔx=F，得滑輪下降的距離為

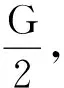
(1)

(2)

兩彈簧伸長量之和Δx=Δx1+Δx2，故重物下降的距離為

綜合應用4，應用5和應用6，我們可以總結出彈簧并聯的特點是每根彈簧的形變量相同．所以彈簧的串并聯有時只是形式上的串并聯，在具體分析題目的時候一定要注意，切忌亂套公式．

3 總結

總之，彈簧串并聯后，系統的性質會發生變化．彈簧的串聯效果類似于電阻的并聯效果，而彈簧的并聯效果類似于電阻的串聯效果．高中物理雖然不要求用公式定量地對彈簧組合的等效勁度系數進行分析，但是彈簧的串并聯的特點要掌握：彈簧串聯時，每根彈簧的彈力相等；原長相同的彈簧并聯時，每根彈簧的形變量相同，這才是解題的根本．對彈簧串并聯問題的分析能夠較好地培養學生的分析、解決問題的能力，我們在教學的過程中，要注意學生思辨能力和思考習慣的培養．

參考文獻

1 漆安慎，杜嬋英.普通物理學·力學.北京：高等教育出版社，2005

2 莊盛文. 彈簧串、并聯略談.物理實驗(中學部分)，2004，24(4)

3 陳學志，羅瑩.探究彈簧勁度系數的影響因素.中國現代教育裝備，2011(8)