基于Schmidt正交單位化的稀疏化定位算法

趙春暉，許云龍，黃輝，崔冰

（哈爾濱工程大學信息與通信工程學院，黑龍江哈爾濱150001）

基于Schmidt正交單位化的稀疏化定位算法

趙春暉，許云龍，黃輝，崔冰

（哈爾濱工程大學信息與通信工程學院，黑龍江哈爾濱150001）

為了提高在一個移動信標節點下的無線傳感器網絡節點定位的精度，提出了一種稀疏化的無線傳感器網絡節點定位算法。該算法通過網格化感知區域把節點定位問題轉化為稀疏信號重構問題，并提出了Schmidt正交單位化的預處理方法，對觀測矩陣進行預處理，使其有效地滿足了約束等距性條件。并針對稀疏定位模型中得到的稀疏信號是近似稀疏信號的問題，采用質心算法來優化算法的定位精度。實驗結果表明，相比于MAP類算法，稀疏化的無線傳感器網絡節點定位算法的定位精度更優，同時所需要的信標節點的廣播次數也更少。

稀疏化定位；節點定位；壓縮感知；Schmidt正交單位化；無線傳感器網絡；移動信標

無線傳感器網絡（wireless sensor network，WSN）是由隨機分布在監測區域內大量的、廉價的、微型的傳感器構成的多跳自組織網絡。WSN以其低功耗、低成本、自組織和分布式等特點為信息感知帶來了一場重大的變革。由于資源和成本的限制，在WSN的多數應用中，除了少數信標節點外，絕大多數節點的位置是未知的。然而，網絡中傳感器的布局、覆蓋、目標定位［1］、目標追蹤［2］等都離不開節點的位置信息，沒有位置信息，網絡的監測消息將毫無意義。因此，確定節點的自身位置是WSN實際應用過程中亟待解決的問題。

根據信標節點的類型，無線傳感器網絡節點定位算法可分為基于靜態信標節點的定位算法和基于移動信標節點的定位算法。由于靜態信標節點在網絡中不能隨機移動，為了使所有的節點都能被準確定位，網絡需要布設大量的靜態信標節點，這樣就會使得系統的功率損耗和網絡的硬件開銷大大地增加。而移動信標節點在網絡中可以動態的移動并在移動過程中廣播位置信息，一個移動信標節點在網絡中的作用等同于多個靜態信標節點。因此，移動信標節點的使用能使網絡成本得到有效地控制。WSN中，典型的基于移動信標節點的定位算法有基于測距［3］的定位算法、HADO［4］定位算法、MAP［5-7］類算法等。其中，基于測距的定位算法是利用節點間的距離信息估計節點的位置，由于算法依靠測距技術，因此需要附加額外的測距設備，增加了系統的硬件開銷；HADO算法通過利用信標節點的到達和離開來估計節點的位置，然而該算法對移動信標節點的移動路徑要求高；MAP類算法通過利用節點感知邊界上的信標點來估計節點的可能位置，但是，該類算法的定位精度易受其選擇的信標點影響。

本文提出了一種新的無線傳感器網絡節點稀疏化定位模型。通過網格化感知區域，將基于移動信標節點的無線傳感器節點定位問題有效地轉化為了壓縮感知［8-9］的問題。在此基礎上，針對觀測矩陣不能滿足RIP［9］問題，提出了Schmidt正交單位化的預處理方法，使得觀測矩陣有效地滿足RIP條件，保證了壓縮感知算法的重構性能。最后，針對模型中信號不是嚴格的1稀疏信號的問題，采用了加權質心算法［10］來進一步改善節點的定位精度。

1 系統模型

1.1 稀疏化定位模型

假設一個節點在其感知區域內，能夠監聽到M個信標點的信號，則可利用這M個信標點來確定該節點的無線感知區域。將所確定的感知區域均勻地劃分成N個網格，由于節點只會存在于其中的一個網格中，將該網格看作1，其他網格看作0。這樣，就可以將節點的定位問題轉化為稀疏度為1的N維向量的重構問題，此時，節點需要根據接收到的信標點的信號最終確定自身所在的網格位置。節點的稀疏化定位模型如圖1所示。

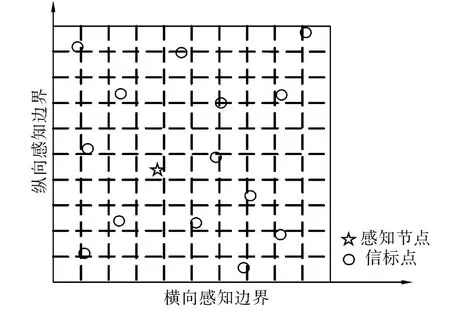
圖1 稀疏化定位模型Fig.1 Sparse localization model

1.2 壓縮感知算法

依據壓縮感知［8-9］理論，未知信號X∈RN在測量矩陣AM×N（M?N）的投影下，可轉換為線性觀測值Y∈RM如下：

壓縮感知的最終目標是將方程組（1）中的未知信號X準確的重構出來。由于上式中Y的維數M遠小于信號X的維數N。因此，此方程組為欠定線性方程組，即方程組有無窮多解。

壓縮感知［8］理論認為：若X為k稀疏的信號，且測量矩陣AM×N滿足RIP條件，則信號X的精確重構可通過求解一個l1范數最小化的問題獲得，過程如式（2）所示：

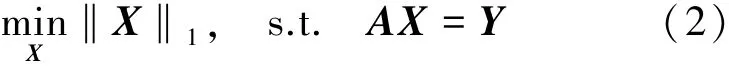
在稀疏化定位模型中，測量矩陣A中第m行第n列元素表示的是第m個信標點到第n個網格中心點的信號接收強度RSSm，n。這樣，稀疏度為1的信號X的壓縮采樣過程可描述如下：

式中：yi（1≤i≤M）為節點接收到第i個信標點的信號強度；在定位模型中，若節點存在于第n個網格中，則xn＝1，其余為0。顯然，未知信號X是1稀疏的。這樣，通過網格化感知區域，節點定位問題就變成了稀疏信號X的重構問題了。

2 SLSO定位算法

2.1 Schmidt正交單位化預處理

由于測量矩陣A是通過信標點與網格之間的信號衰減模型得到，因此，A中元素較為相關，即無法滿足等距約束條件。為此，本文利用Schmidt正交單位化對測量矩陣進行預處理，得到的新的測量矩陣能有效地滿足RIP條件，從而保證算法的重建性能。

Schmidt正交單位化預處理包括正交化和單位化2個過程。首先，正交化測量矩陣A的過程如式（4）所示：

式中：A1，A2，…，AM為測量矩陣A的行向量，且有Am＝［RSSm，1，RSSm，2，…，RSSm，N］表示第m個信標點到每一個網格中心點的信號接收強度；〈·，·〉表示內積算子；T是一個對角線元素全為1的下三角矩陣；通過正交化后得到矩陣B的正交向量組B1，B2，…，BM。然后，對矩陣A進行行單位化得

式中：‖·‖指的是矩陣的模值。因此，矩陣Q是行向量相互正交的單位向量。

最后，列單位化矩陣Q，即得新的測量矩陣Φ如下：

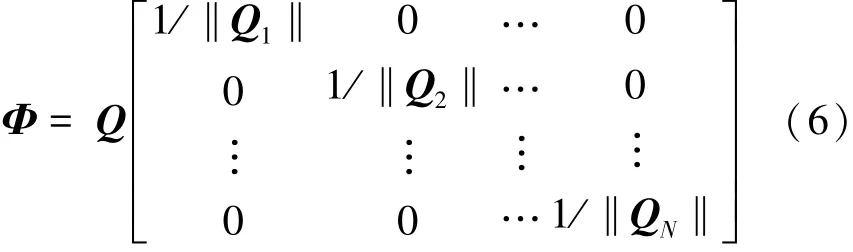
式中：Q1，Q2，…，QN為矩陣Q的列向量。由于Q的行向量是相互正交的單位向量，且Φ是通過列單位化Q得到。因此，Φ是壓縮感知理論中常用的觀測矩陣之一的部分正交矩陣［8］。換句話說，Φ是完全滿足等距約束條件的。

令T1＝diag（‖B1‖，‖B2‖，…，‖BM‖）。對觀測值Y進行下面的變換可得新的觀測值Y′：

Y′＝（TT1）?Y＝（TT1）?AX＝（TT1）?TT1QX＝

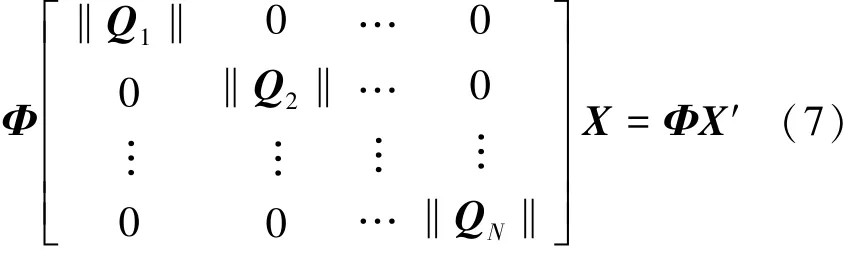
式中：（·）?表示矩陣的逆運算。由式（7）可知：

顯然，X′是由矩陣X左邊乘一個對角矩陣得到，由于稀疏化定位模型中的未知信號X是稀疏的，因此X′也是稀疏的，且其稀疏度與X相等。又由于Φ完全地滿足等距約束條件，因此，X′能夠依據壓縮感知理論被準確地重構出來，這樣，原信號X也就被確定了。

2.2 節點位置估計

在稀疏化定位模型中，理論上將每個網格的中心位置作為該網格的坐標。然而，在實際的WSN應用場景中，節點是隨機分布的，換句話說，節點的位置不一定在網格的正中心。因此，實際的X應該是一個近似的稀疏度為1的稀疏信號。為了減小定位誤差，本文采用加權質心算法［10］估計節點的位置。

首先，歸一化信號X，得到每個網格對該節點估計位置的權值ωn：

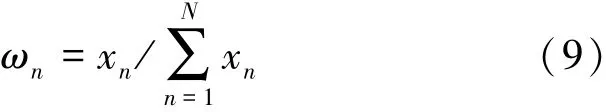
式中：ωn為第n個網格對該節點估計位置的權值大小。然后，利用加權質心算法求解該節點的估計位置，如式（10）所示：

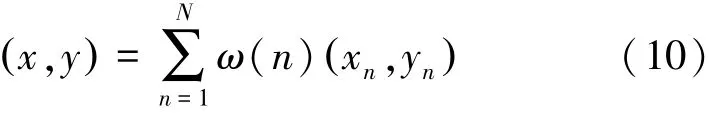
式中：(x，y)表示節點的估計位置，(xn，yn)表示第n個網格的中心所在的位置。

2.3 感知區域的確定

稀疏化定位模型首先需要對節點的感知區域進行網格化，因此，節點感知區域的確定是節點定位的基本前提。然而，WSN中待定位的節點自身是無法確定其感知區域的，這時，在節點感知區域內的一些位置信息已知的信標點則能發揮其關鍵作用，即可利用這些信標點來確定節點的感知區域。為了使節點感知區域的覆蓋范圍盡可能的小，MCB（monte carlo localization boxed）定位算法［11］利用信標盒子的思想對感知區域進行確定。然而，該信標盒子并沒有將所有的信標點包含到感知區域內。因此，為更準確地確定感知區域坐標，本文對其進行如下改進：

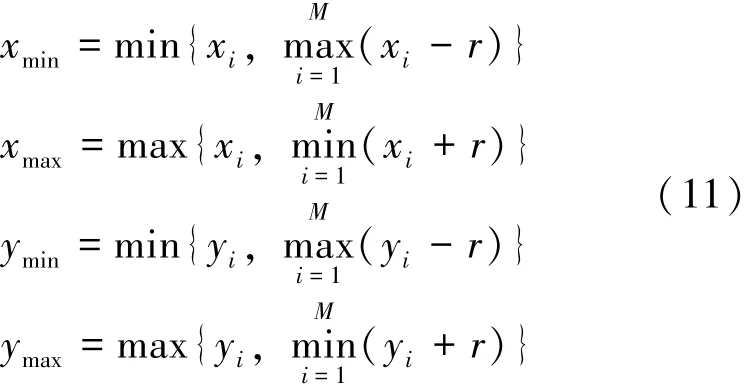
式中：xmin、xmax、ymin、ymax分別表示感知區域的x軸，y軸坐標的最小值和最大值；xi和yi分別為第i個信標點的x軸和y軸坐標；r為節點的通信半徑；M是節點感知到的信標點的個數。

2.4 信標點個數的選擇

由于在感知區域內，節點能感知到的信標點的個數可能非常多，這將給普通節點帶來很大的計算負擔。此外，由文獻［8］可知：當M大于等于O（C· k·μ2·（logN）4）時，算法已經能準確地重建出原信號，其中k是信號的稀疏度，C是一個常數，μ＝Nmax |Φi，j|，這也就是說，信標點個數達到一定

i，j值后，過多的信標點對節點定位精度的提升并不明顯。因此，合理的選擇信標節點個數是非常必要的。為便于合理取值信標點個數，本文把普通節點的稀疏化定位模型抽象成為在一個方形的無線感知區域內定位某一固定目標的問題。

假設在一個20 m×20 m的方形感知區域內，隨機地分布著M個傳感器，將感知區域均勻地網格化為15×15的小格子。則在信標點的發射信號強度為-40 dBm，信噪比為20 dB的環境下，對2～10的每一個固定的M值進行100次仿真，取節點定位誤差的平均值作為其平均定位誤差，得到如圖2所示的目標平均定位誤差隨傳感器個數M變化的曲線。從圖中曲線可以看出：節點的平均定位誤差隨傳感器個數M的增加而降低。然而，當傳感器個數M≥4時，目標的平均定位誤差均保持在0.5 m左右；當M≥8時，目標的平均定位誤差已基本無變化。

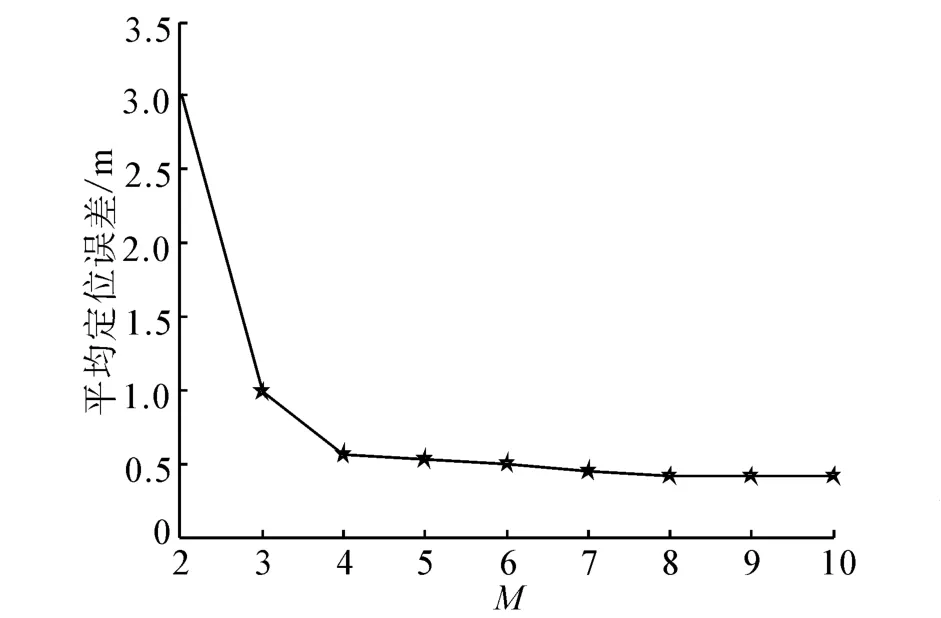
圖2 定位精度與傳感器個數的關系Fig.2 Relationship between localization accuracy and number of nodes

3 仿真結果和分析

為了驗證算法的有效性，利用MATLAB對SLSO算法進行了仿真，并將其與MAP+GC［6］、MAPM［7］和MAP-M＆N［7］算法的定位精度進行對比。其中，假設在一個邊長為100 m的方形感知區域內隨機地分布著1 000個普通節點，網絡中所有的普通節點和信標節點的通信半徑均為20 m，信標節點最大移動速度為20 m／s，且其移動路徑遵循RWP［12］模型。此外，在SLSO算法中，將節點感知區域均勻地劃分為15×15的網格，信標點的發射信號強度為-40 dBm，信噪比為20 dB。當節點感知到的信標點個數大于或等于8時，則取其中信號強度最強的8個信標點進行定位，即M＝8，否則M為實際感知到的信標點個數。在SLSO算法中，設定信標節點每1 s廣播一次信標信號，廣播400次。而在MAP類算法中，由于信標點廣播間隔太大會影響定位精度，因此，設定信標節點每0.1 s廣播一次信標信號，廣播10 000次。

本文采用文獻［13］中的信號衰落模型，則有距離信號源為d時感知節點接收到的信號強度為

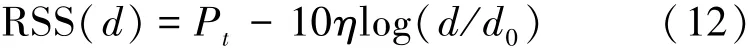
式中：Pt為距離信號源節點為d0的節點接收到的信號強度，η為衰減指數，通常取2～4，本文取2。

3.1 理想環境下的定位精度對比

在MATLAB仿真環境下，對SLSO、MAP+GC、MAP-M和MAP-M＆N 4中算法在理想環境中的節點位置誤差進行對比如圖3所示。圖3中的圓圈表示該節點未被定為到。通過比較可以看出：SLSO算法定位的大部分節點定為誤差均小于5 m，即使最大的誤差也只有15 m左右。而MAP類定位算法中，有較多的節點存在很大的定位誤差，最大的甚至超過了30 m。此外，MAP類算法即使信標節點廣播了10 000次，也依然存在定位不到的節點。這是由于MAP類算法需要選擇合適的信標點進行定位，否則會對節點定位產生較大的影響，甚至在沒有合適的信標節點的情況下，無法完成節點的定位。而SLSO算法只有當接收到的信標點較少時，其定位精度才會較差，并且算法對信標點沒有特定的要求。

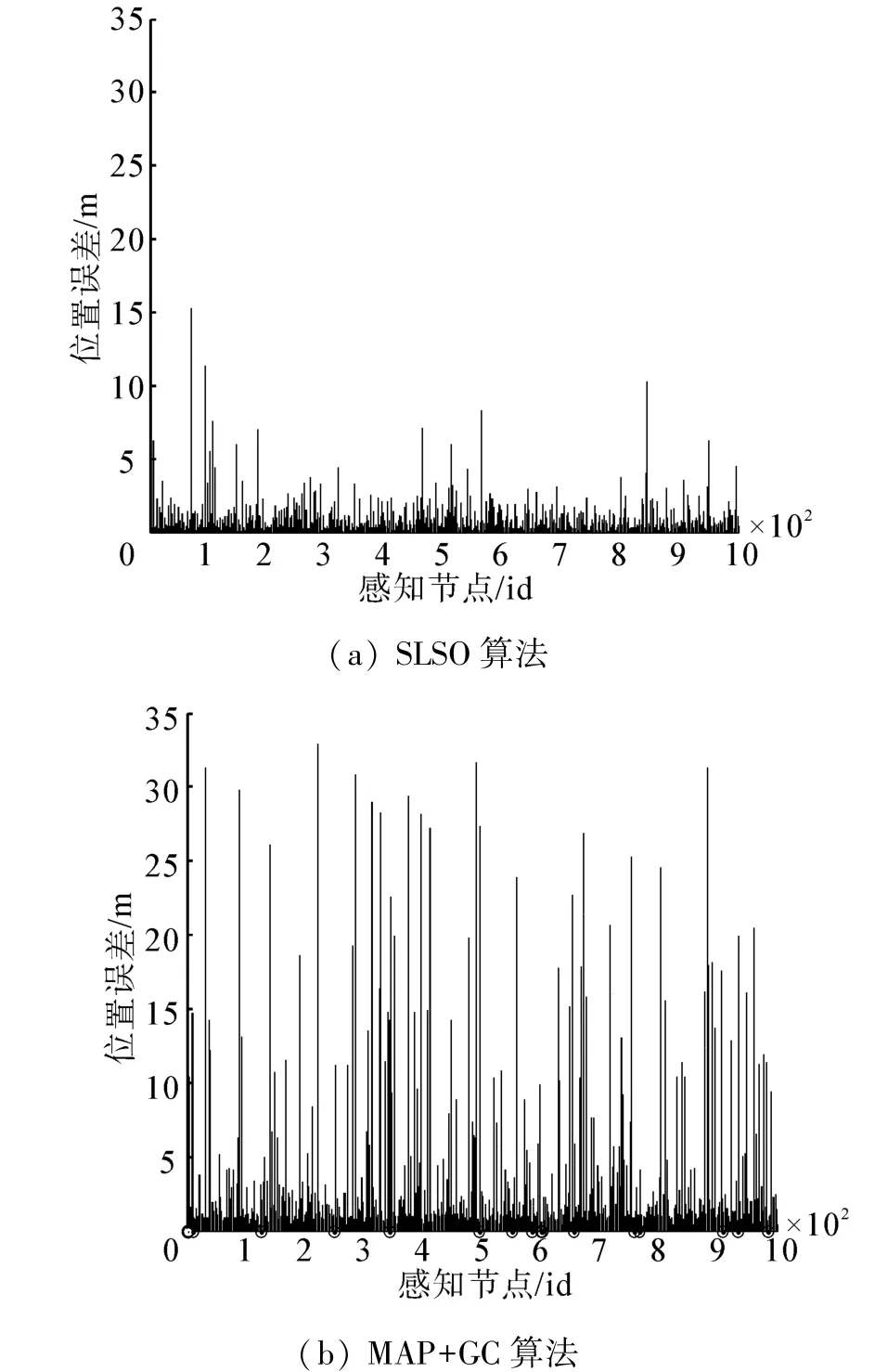
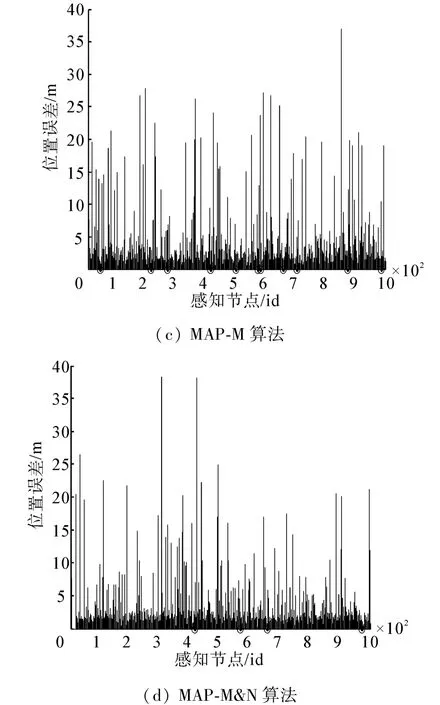
圖3 算法定位精度對比Fig.3 The localization accuracy comparison

3.2 通信半徑對定位精度的影響

如表1所示定量的比較了理想環境中4種算法在不同的通信半徑下的定位精度。從表中數據可以看出：在相同的節點通信半徑下，SLSO算法的平均定位誤差遠小于MAP類算法。此外，對同一種定位算法而言，隨著通信半徑的增加，節點的平均定位誤差也在逐漸的增加，這是由于半徑增大，對節點的約束性越來越小，因此誤差也越來越大。

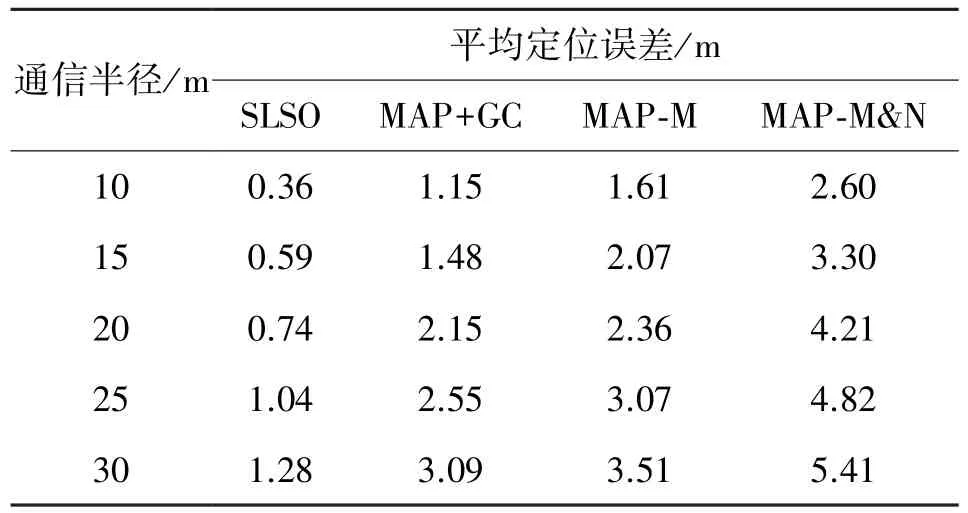
表1 通信半徑對算法定位精度的影響Table1 The impact of radio range on the localization accuracy

3.3 障礙物環境下的定位精度對比

在實際WSN應用環境中，節點定位往往會受到各種障礙物的影響，因此，本節將進一步的分析算法在障礙物環境下的定位精度。障礙物環境下的節點分布圖如圖4所示。

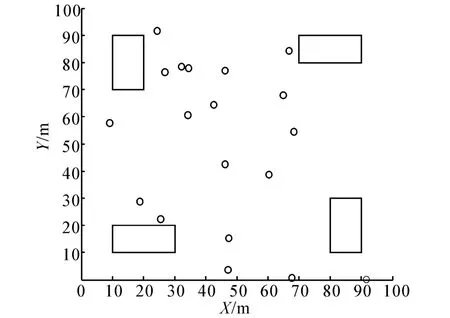
圖4 障礙物環境下的節點分布圖Fig.4 The distribution of nodes with obstacles

在如圖4所示的障礙物環境下，對4種算法的定位精度進行MATLAB仿真實驗，得到如表2所示的障礙物環境下各算法的平均定位誤差。

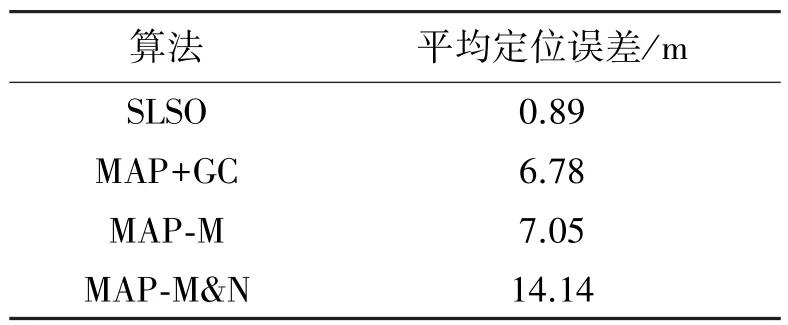
表2 障礙物環境下算法的定位精度對比Table 2 The localization accuracy comparison under obstacle environment

從表2中數據可知：即使在障礙物環境下，SLSO算法的節點平均定位誤差依然要遠小于MAP類算法，也就是說，相比于MAP類算法，不論是在理想環境下還是在存在障礙物的環境中，SLSO算法都是一個更好的選擇。此外，通過對比表1和表2可以看出：在障礙物存在的情況下，MAP類算法的性能下降的比較厲害，而SLSO算法的平均定位誤差波動不大。這是MAP類算法中靠近障礙物的節點選擇了錯誤的信標點，這樣，會影響其弦方位，進而影響到節點的定位精度，其中在MAP-M＆N算法中表現尤甚，這是因為其節點定位本身存在著定位誤差，而該算法還利用了這些存在定位誤差的已定位節點去定位其他還未被定位的節點，因此其很有可能會錯誤的選擇節點可能位置。而在SLSO算法中，障礙物的存在僅使得靠近障礙物的節點所能接收到的信標點個數減少了，因此其定位精度僅受到較小的影響。

3.4 GPS定位誤差對定性性能的影響

WSN中，信標節點依賴于GPS設備進行自身的定位，然而，實際應用中GPS設備往往也會存在一定的定位誤差。在信標節點GPS誤差標準差為0.05 m，GPS誤差均值分別為0、0.1、0.2、0.3、0.4 m時，對4種算法的定位精度進行仿真實驗對比如圖5所示。由圖中曲線可知：4種算法的定位精度均隨著GPS平均定位誤差的增大而緩慢的降低。而在相同的GPS誤差均值的條件下，SLSO算法在平均定位誤差要遠優于MAP類算法。此外，通過表1和圖5可以看出：信標節點的GPS誤差對算法的定位精度并沒有較大的影響。

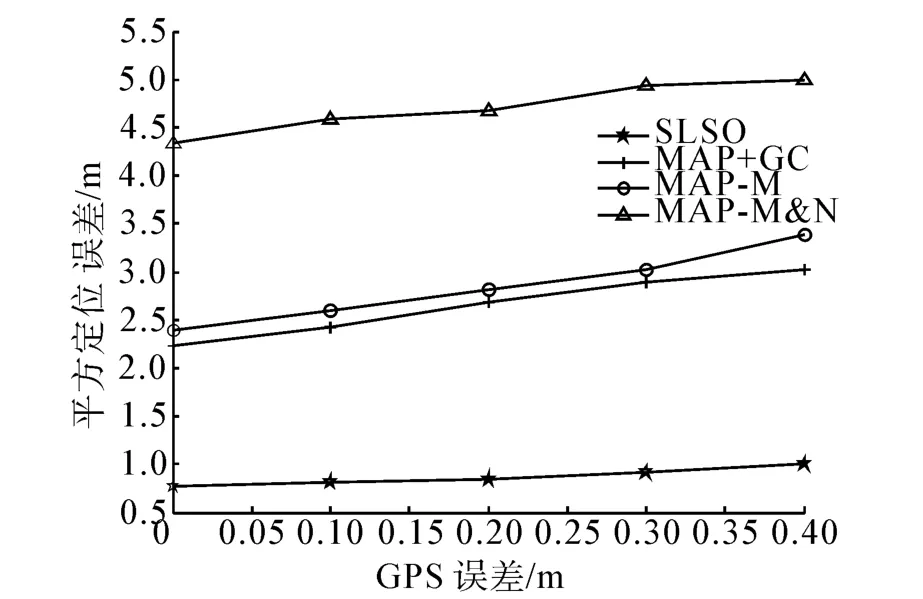
圖5 GPS誤差對定位精度的影響Fig.5 The impact of GPS error on the localization accuracy

3.5 通信半徑不規則性對定性性能的影響

在實際環境中，節點的通信半徑具有一定的不規則性（degree of irregularity，DOI）。DOI是指節點的最大通信半徑在不同的角度和方向上具有不同程度的衰減，衰減因子［14］如下：

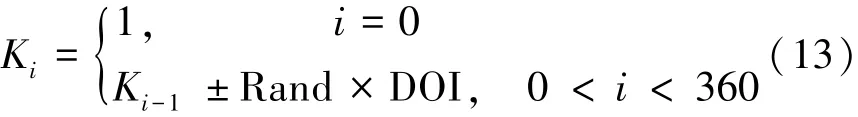
其中：K0-K359≤DOI。

圖6對比分析了通信半徑的不規則性對算法定位精度的影響。

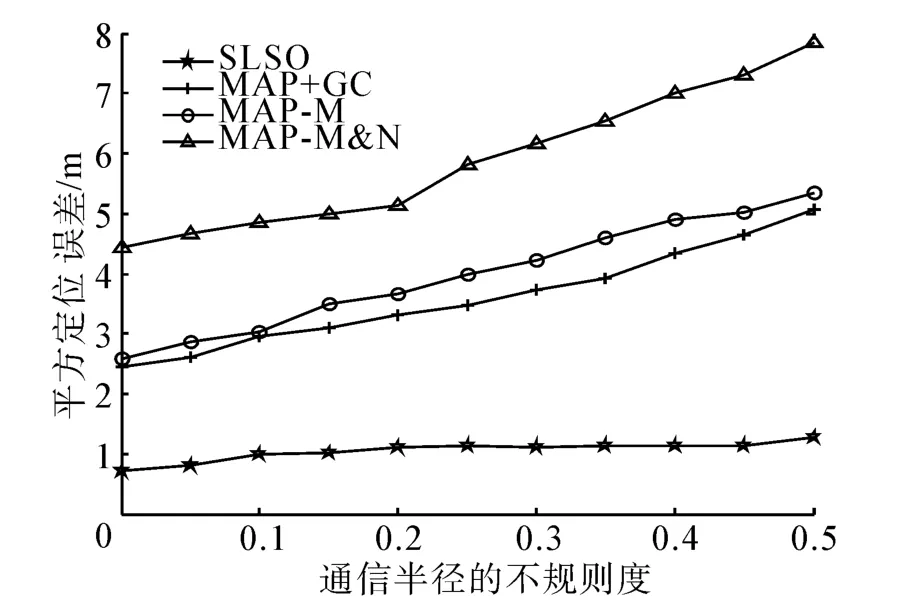
圖6 定位精度與通信半徑的不規則度的關系Fig.6 Relationship between localization accuracy and DOI

圖中曲線表明：4種算法的定位精度均隨著通信半徑不規則度的增大而降低。而在相等的通信半徑不規則度下，SLSO算法的平均定位誤差遠小于MAP類算法。此外，通信半徑不規則度對SLSO算法的影響遠小于MAP類算法。這是由于SLSO算法采用的是信號接收強度進行節點定位，因此通信半徑的不規則性對其基本上沒什么影響，而MAP類算法需要利用通信半徑估計節點的位置，因此通信半徑的不規則性，將會嚴重地影響算法的定位精度。

3.6 噪聲對定位精度的影響

如表3所示是在不同信噪比下仿真了SLSO算法的定位精度。由表中數據可知：算法的平均定位誤差隨著信噪比的增大而不斷減小，即算法的定位精度越來越好。這是由于信噪比越大，節點接收到的信號強度越準確，因此算法的性能越好，反之亦然。同時，通過對比表3和表1可知：即使在0dB的信噪比環境下，SLSO算法的定位精度仍優于MAP類算法。因此，在復雜環境下，SLSO算法仍然是一個較好的選擇。

表3 噪聲對SLSO算法定位精度的影響Table 3 The impact of noise on SLSO localization accuracy

4 結束語

本文提出了基于Schmidt正交單位化的稀疏化定位算法。首先，算法通過網格化感知區域，首次把只存在一個移動信標節點的無線傳感器網絡的節點定位問題轉換為了稀疏度為1的N維向量重構問題；然后，為使測量矩陣完全有效地滿足RIP性質，提出了Schmidt正交單位化的預處理方法，保證了算法的壓縮感知重建性能；最后，利用質心算法準確地估計節點位置。仿真結果表明：相比于MAP類算法，SLSO算法有更小的平均定位誤差，也就是說，SLSO算法的定位精度遠優于MAP類算法。與此同時，定位所有的節點，SLSO算法需要的信標點個數遠少于MAP類算法，且障礙物和通信半徑不規則性對SLSO算法無明顯影響。并且，在信噪比很低的情況下，SLSO算法仍然優于MAP類算法。因此，SLSO算法具有更強的適應性和實用性。

［1］趙春暉，許云龍.能量約束貝葉斯壓縮感知檢測算法［J］.通信學報，2012，33（10）：1-6.ZHAO Chunhui，XU Yunlong.Energy constraint Bayesian compressive sensing detection algorithm［J］.Journal on Communications，2012，33（10）：1-6.

［2］WANG Xingbo，FU Minyue，ZHANG Huanshui.Targettracking in wireless sensor networks based on the combination of KF and MLE using distance measurements［J］.IEEE Transactions on Mobile Computing，2012，11（4）：567-576.

［3］SICHITIU M L，RAMADURAI V.Localization of wireless sensor networks with a mobile beacon［C］／／IEEE International Conference on Mobile Ad-hoc and Sensor Systems.Raleigh，USA，2004：174-183.

［4］XIAO Bin，CHEN Hekang，ZHOU Shuigeng.Distributed localization using a moving beacon in wireless sensor networks［J］.IEEE Transactions on Parallel and Distributed Systems，2008，19（5）：587-600.

［5］SSU K F，OU C H，JIAU H C.Localization with mobile an

chor points in wireless sensor networks［J］.IEEE Transac

tions on Vehicular Technology，2005，54（3）：1187-1197.［6］LEE S，KIM E，KIM C，et al.Localization with a mobile beacon based on geometric constraints in wireless sensor networks［J］.IEEE Transactions on Wireless Communications，2009，8（12）：5801-5805.

［7］LIAO W H，LEE Y C，KEDIA S P.Mobile anchor positioning for wireless sensor networks［J］.IET Communications，2011，5（7）：914-921.

［8］CADES E.Compressive sampling［J］.International Congress of Mathematicians，2006，3：1433-1452.

［9］CADES E，PLAN Y.A probabilistic and RIP less theory of compressed sensing［J］.IEEE Transactions on Information Theory，2011，57（11）：7235-7254.

［10］WANG Jun，URRIZA P，HAN Yuxing，et al.Weighted centroid localization algorithm：theoretical analysis and distributed implementation［J］.IEEE Transactions on Wireless Communications，2011，10（10）：3403-3413.

［11］ALINE B，KOEN L.Monte-Carlo Localization for mobile wireless sensor networks［J］.Ad Hoc Networks，2006，6（5）：718-733.

［12］BROCH J，MALTZ D A，JOHNSON D B，et al.A performance comparison of multi-hop wireless Ad hoc network routing protocols［C］／／ACM International Conference on Mobile Computing Networking.Dallas，USA，1998：85-97.

［13］PATWARI N，ASH J N，KYPEROUNTAS S，et al.Locating the nodes：cooperative localization in wireless sensor networks［J］.IEEE Signal Processing Magazine，2005，22（4）：54-69.

［14］HE T，HUANG C，BLUM M B，et al.Range-free localization schemes for large scale sensor network［J］.ACM Transactions on Embedded Computing System，2005，4（4）：877-906.

Sparse localization on the basis of Schmidt orthonormalization in wireless sensor networks

ZHAO Chunhui，XU Yunlong，HUANG Hui，CUI Bing
（College of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China）

To improve the localization accuracy of a node in the wireless sensor network with a mobile beacon node，a sparse localization algorithm using Schmidt orthonormalization（SLSO）was proposed.With the SLSO，the node localization problem was converted to a reconstruction problem of the sparse signal by gridding the sensing area，and a new observation matrix which is able to effectively satisfy the restricted isometry property（RIP）was obtained by Schmidt orthonormalization.To solve the problem of the sparse signal being approximately sparse in the model，a centroid algorithm was adopted to improve the localization accuracy.The experiment results show that，compared with MAP algorithms，SLSO has better localization accuracy，and requires less broadcasting times.

sparse localization；node localization；compressed sensing；Schmidt orthonormalization；wireless sensor network；mobile beaconing

10.3969／j.issn.1006-7043.201305076

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201305076.html

TP393

A

1006-7043（2014）06-0747-07

2013-05-30.網絡出版時間：2014-05-14 15：53：57.

國家自然科學基金資助項目（61077079）；黑龍江省自然科學基金資助項目（ZD201216）；哈爾濱市優秀學科帶頭人基金資助項目（RC2013XK009003）.

趙春暉（1965-），男，教授，博士生導師.

趙春暉，E-mail：zhaochunhui＠hrbeu.edu.cn.