大震下防屈曲支撐鋼框架彈塑性位移統計規律

郭小康

(上海寶冶集團有限公司，上海 200941)

0 引言

目前，世界各國建筑抗震設計規范普遍采用的“小震不壞、中震可修、大震不倒”的設防水準，是處理地震作用高度不確定性的較為科學合理的對策［1］。按現有抗震規范設計的房屋，能基本避免由于房屋倒塌造成的人員傷亡，但難以有效控制結構在地震作用下的破壞程度，可能導致結構使用功能的喪失，從而引起巨大經濟損失。由于地震在時間、強度和空間上的強隨機性，以及結構材料強度、設計和施工中的人為不確定性因素，結構的性能在地震作用下也具有很大的不確定性。因此，需要把可靠度理論應用到結構抗震性能化設計中，這一點，在美國聯邦緊急救援署(FEMA)的研究報告中也明確提出:“結構的抗震性能化設計框架應該是基于可靠度理論的”［2］。而基于位移的抗震設計是實現抗震性能化設計思想的一個重要途徑［3］。

中心支撐—鋼框架體系，在地震作用下，難以避免支撐受壓屈曲。傳統鋼支撐屈曲后，性能退化嚴重，極易造成支撐本身與節點連接的破壞，進而導致結構抗震能力急劇下降，對結構抗震十分不利。防屈曲支撐拉壓性能相當，滯回曲線飽滿穩定，其不但可作為結構構件，屈服后也是一種性能優良的阻尼器，保護主體結構，降低了結構地震響應。防屈曲支撐鋼框架的應用越來越廣泛，因此有必要獲取其在罕遇地震下的結構位移反應，為該類結構的抗震可靠度設計提供依據。

1 抽樣結構選取

進行結構可靠度分析的首要條件是獲取結構反應量的統計特征，即其概率分布模型與統計特征參數值。取結構的彈塑性位移作為破壞指標，且將結構破壞界限視為定值，即結構的頂層位移或結構層間位移限值;而結構的反應量(結構頂層位移或層間位移)是隨機變量。結構彈塑性位移反應的隨機性與地震波的隨機性以及結構自身的隨機性均相關。地震波的隨機性主要與地震波的峰值加速度PGA、持時、頻譜特性等相關，而結構自身的隨機性與結構材料強度、結構布置形式、結構周期等相關。由于材料的隨機性較地震的隨機性小很多，在此視其為確定值。

在統計分析中取1層，3層，6層，9層，12層5種層數的三跨防屈曲支撐鋼框架進行彈塑性時程分析，結構的初始彈性周期從0.2 s～1.8 s，涵蓋了短、中、長周期。抽樣結構的跨度取為6 m(三跨)，底層層高4 m，其他層層高3.6 m;每層恒載取為5 kN/m2，活載取為2 kN/m2，主體結構用鋼為Q345B，人字形防屈曲支撐核心鋼材為Q235B，布于中跨。根據《建筑結構荷載規范》中荷載組合原則進行荷載組合，按照9度設防，首先對結構進行了小震彈性設計，對結構進行彈塑性時程分析時，取恒載與0.5倍的活載組合作為初始豎向力施加于結構，材料強度取標準值。

2 抽樣地震波選取

為充分體現地震波的隨機性，收集了大量我國、美國的強震記錄以及部分人工地震波，作為結構彈塑性時程分析時所用輸入地震波，分析時按照《建筑抗震設計規范》將地震波峰值加速度PGA調整為620 gal。并根據場地特征周期將地震波分為4類，每類場地選取30條地震波，共計120條，地震波阻尼比為0.05。

3 彈塑性位移統計規律

通過對結構頂層、樓層、層間彈塑性位移與最大彈塑性位移進行K-S假設檢驗，發現它們基本上均服從對數正態分布。以12層防屈曲支撐鋼框架在Ⅳ類場地上的結構反應為例，分別給出其累積概率分布與頻率直方圖，并給出與其同均值和方差的對數正態分布的概率分布函數與概率密度函數，見圖1，發現兩者十分接近。

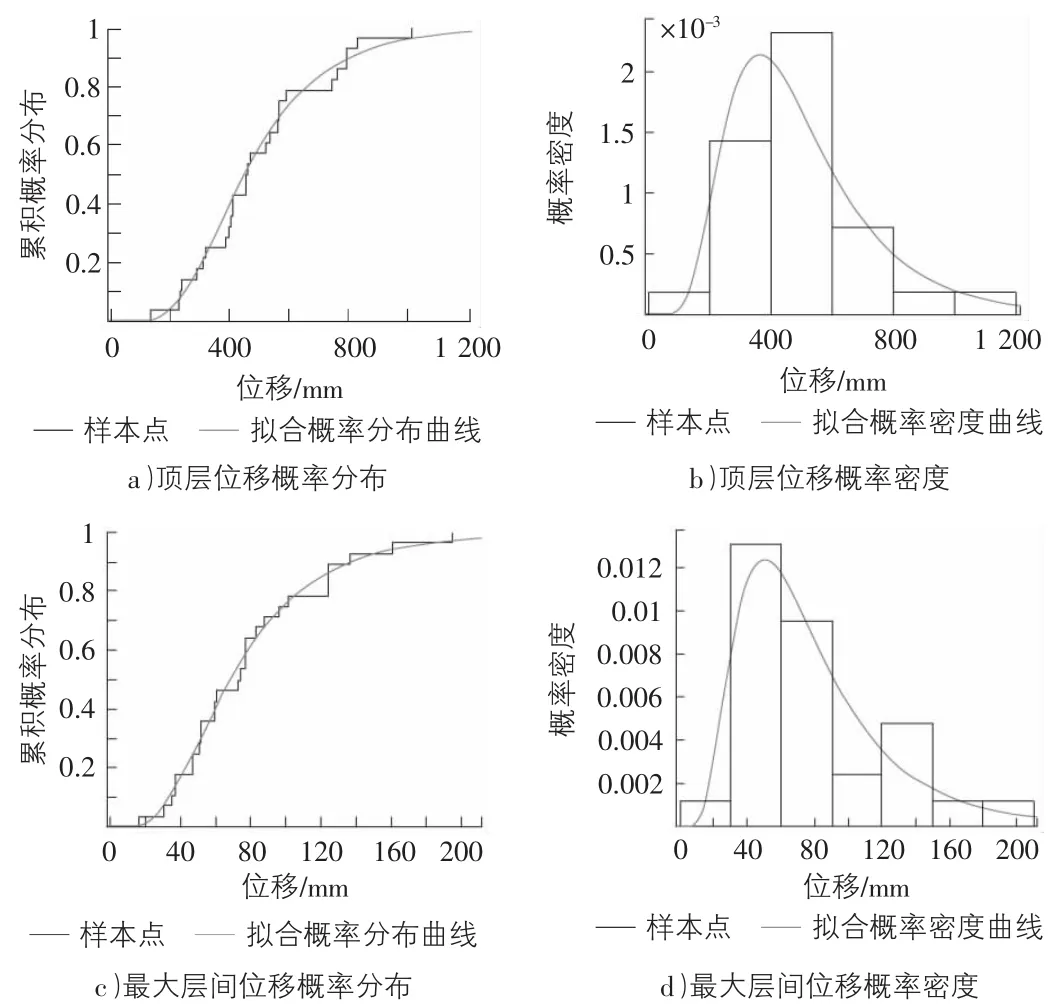
圖1 結構彈塑性位移反應概率特征

采用最小二乘法，對結構頂層位移的變異系數δλt與最大彈塑性層間位移變異系數δλi進行擬合，擬合結果見表1和表2，以及圖2與圖3，A，B為擬合參數，T為結構基本周期。

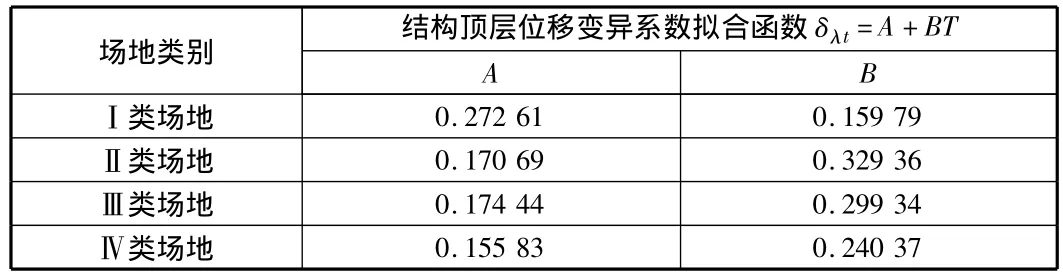
表1 δλt最小二乘法擬合結果

通過統計分析，還可以得到如下主要結論:

1)防屈曲支撐鋼框架的彈塑性頂層位移、樓層位移、層間位移與最大層間位移均大體上服從對數正態分布。

2)樓層位移的變異性隨著層高的增加有減小趨勢，頂層彈塑性位移的變異性最小;而隨著結構總層數的增加，頂層彈塑性位移的變異性將會逐步增大。

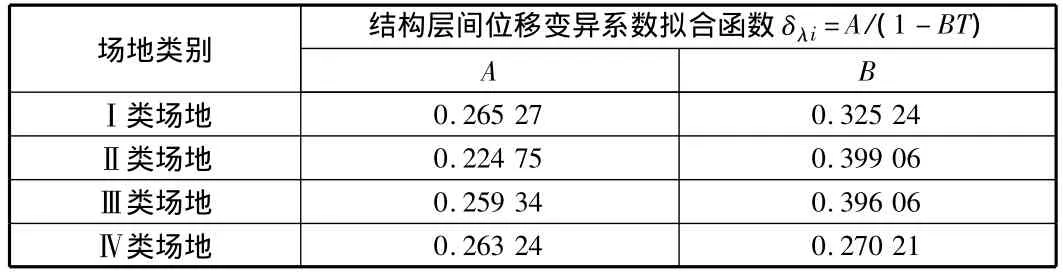
表2 δλi最小二乘法擬合結果

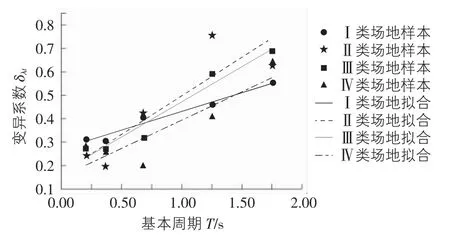
圖2 頂層彈塑性位移變異系數擬合結果

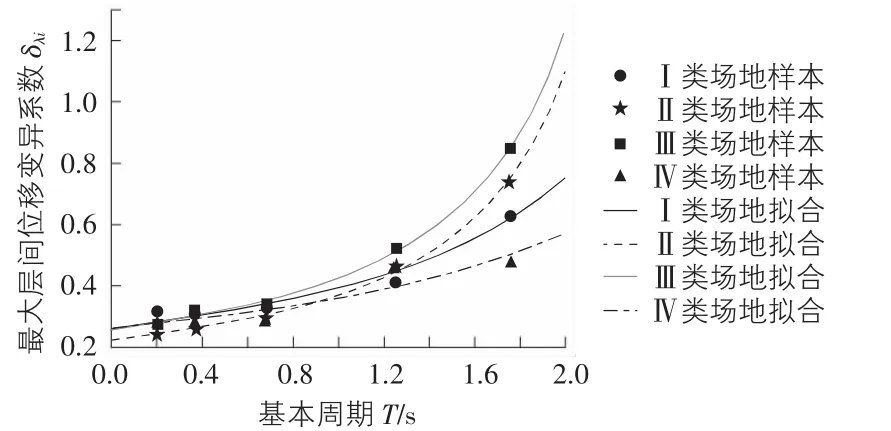
圖3 最大彈塑性層間位移變異系數擬合結果

3)結構層間位移的變異性隨層高的增加總體上也有減小趨勢，但在塑性變形集中的樓層變異系數較大。

4)對于不同場地類別，結構的層位移與層間位移的變異性與結構基本周期與場地特征周期有較強的相關性，即結構基本周期處于場地特征周期范圍內時，層位移與層間位移的變異性較大，但樓層位移的均值Ⅳ類最大，Ⅰ類場地最小。

5)最大彈塑性層間位移出現樓層并不完全相同，總體上較為一致，其變異性也隨著樓層的增加有增大趨勢。

［1］李 剛，程耿東.基于性能的結構抗震設計——理論、方法與應用［M］.北京:科學出版社，2004.

［2］Federal Emergency Management Agency.NEHRP guidelines for the seismic rehabilitation of buildings［R］.FEMA 273.FEMA 274.Commentary.Washington(DC)，1996.

［3］馬宏旺，呂西林.建筑結構基于性能抗震設計的幾個問題［J］.同濟大學學報，2002，30(12):1429-1434.