金融風險測度模型及其蘊含的金融風險主觀性

張秀麗

（鄭州大學 商學院，河南鄭州 450001）

一、引言

金融風險所造成的影響是令人矚目的，金融危機所帶來的后果也是嚴重的，它有時會導致全球經濟衰退，甚至造成主權危機。較近的是2007～2008年的全球金融危機，它直接導致一些著名金融機構破產，譬如美國最大的儲蓄及貸款銀行華盛頓互惠倒閉，這是美國有史以來倒閉的最大銀行;保險大亨AIG在2008年第四季度創下了美國公司歷史上最大的虧損，金額高達617億美元，而倒閉的還有著名的投資銀行雷曼兄弟。

而金融風險管理離不開良好的金融風險測度，只有金融風險測度準確，風險管理才有可靠依據。但是金融風險種類繁多，相應的金融風險測度模型也各不相同。根據Basel協議的分類，金融機構風險主要分為市場風險、信用風險、流動性風險和操作風險。風險不同，服從的分布也有所差異，如有些風險近似服從正態分布，而有些則需用極值理論才能描述。本文根據金融風險的分類討論了主要的金融風險測度模型，并在介紹模型的基礎上分析了其蘊含的主觀性，建議進行風險管理時要考慮其主觀性特征，使風險管理的目標與股東利益最大化一致。

二、市場風險測度模型及其主觀性

Dowd認為市場風險是指市場價格的不可預期變化導致的損益的風險〔1〕。根據風險因素的不同，市場風險又可以分為利率風險、股權風險、匯率風險和大宗商品價格風險，其他的金融風險如信用風險和操作風險也會導致市場風險。

（一）市場風險測度模型

主要的市場風險測度有缺口分析、久期和凸性分析、希臘值、風險價值、一致風險測度和跌幅風險等。

1．缺口分析

較早的風險測度是缺口分析，即根據在一定的時間區間內資產與負債的重新定價，得到利率敏感性資產和負債的數值，二者的差額就是缺口值，

式中，RSA為利率敏感性資產，RSL為利率敏感性負債。

GAP越大，表明利率變動帶來的收入的變動越大，風險也就越大。相應的風險敞口為

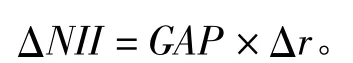
式中，Δr為利率變化。

2．久期和凸性分析

另一個測度風險的方法是久期〔2〕，即

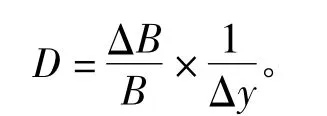
式中，B為債券價格，Δy為收益率的變化。

久期越大，債券價格對收益率的變化越敏感，風險越大。

采用久期作為風險度量只適合于收益率發生微小變化的情況，如果收益率變化較大，則需要采用凸性〔3〕對其進行修正，債券價格變動的百分比為

3．希臘值——σ、β、δ、Γ、ρ、θ、Vega

自從Markowitz的投資組合理論提出來之后，風險測度有了新的進展，即用標準差σ來度量風險〔4〕。標準差越大，風險越大。投資者根據自己的風險容忍程度進行證券投資選擇，如果風險容忍程度高，就選擇高風險高收益的證券，否則就選擇低風險低收益的證券。

Sharpe將Markowitz的理論進一步發展，提出著名的CAPM模型〔5〕，這時單個資產的風險不再是其收益率的標準差，而是該資產的風險對整個資產組合風險的貢獻，即

除了β之外，還有其他的希臘值測度風險，主要用于衍生品，如 δ、Γ、ρ、θ;另外還有一個不是希臘字母的Vega，這類測度只在風險因素發生微小變化時起作用。

4．風險價值

風險價值是當前應用得比較多的一種風險測度方法〔6～7〕，它采用分位數作為風險測度。如果qα為某證券組合的持有期收益的α分位點，那么，在給定置信水平1－α的情況下，持有期內的風險價值為

可見，決定風險價值大小的是置信水平大小與持有期長短。

5．一致風險測度

一致風險測度是Artzner等在1997、1999年提出來的〔8～9〕〕，它認為風險測度f（）應該滿足以下性質：

（1）單調性：X≥Y?F（X）≤f（Y）;

（2）次可加性：f（X+Y）≤f（X）+f（Y）;

（3）正齊次性：f（λX）=λf（X）;

（4）平移不變性：f（x+c）=f（X）－c。

在一致風險測度中，次可加性是最重要的。它意味著把單個的風險資產組合在一起時，總的風險會減少，或者至少不會增加。如果不滿足次可加性，就會出現一些尷尬的結果，比如風險的加總小于組合的風險，即f（X+Y）＞f（X）+f（Y）。如果監管者據此設定資本金要求，那么金融機構會將自己拆分為更小的單位以減少資本金，這顯然是不合適的。

6．跌幅風險

Chekhlov等于2003 年提出跌幅風險〔10～11〕，它是關于最壞的α的跌幅DDown的平均值，跌幅是相對于運行最大值①的損失。

條件風險跌幅為

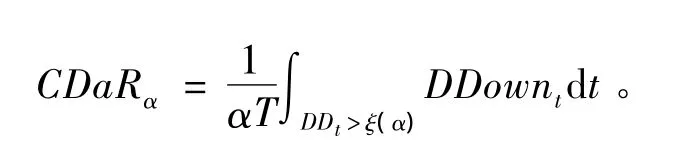
（二）市場風險測度模型的主觀性

市場風險模型的發展經歷了一個從簡單到復雜，從考慮一種風險因素到考慮多種風險因素的過程，且隨著計算機的發展，模擬開始出現，這使得模型蘊含的主觀性在逐漸增加。

風險缺口分析計算簡單，易于操作，但是它只能用于估算資產負債表內的風險，而且是粗略估算，對區間范圍很敏感。該模型只關心利率變化對收入的影響，而不關心對價值的影響。

久期雖然計算方便，容易操作，但是它只度量了利率風險，忽略了其他風險。不過久期分析優于缺口分析，因為它關注資產或負債本身價值的變化，而不只是收入的變化。二者的區別在于時間因素的引入，即，利率的變化和收益率的變化。而時間因素的引入是具有心理學背景的，即人們推遲消費應得到補償，而補償的大小是有主觀性的。

使用均值—方差框架下的風險測度指標度量風險時，可以同時考慮多個資產的風險，而不是單一資產風險，但是，該度量的一個重要的假設是收益率的分布服從正態分布。不幸的是，實證研究表明，收益率的分布是尖峰厚尾的，即尾部事件發生的概率較大。因此使用該類模型測度風險時，首先在主觀上設定了收益率的分布，其次，市場收益率也具有很強的主觀性，選擇不同的指數作為市場的代表，其收益率是不同的。

采用VaR作為風險測度模型對證券收益率的分布沒有要求，相對于均值—方差框架更為實用。但是VaR不能告訴我們一旦超過α分位點的事件發生，可能的損失將有多大。這意味著，如果兩個證券組合具有相同的VaR，可能面臨不同的風險暴露。實際上，VaR在橢圓分布下表現很好，而在其他分布下的表現是不可靠的。因此，采用該模型的主觀性首先表現在對證券收益的假設，其次是置信水平的考慮，置信水平越高，VaR就越大，反之亦然;再次是時間區間的選擇，一般是通過單日VaR計算較長時期的VaR，即

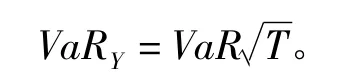
通過這種方式計算的VaR可能高估風險，所以在較長時期內VaR的估計變得不可靠。

VaR還有一個重要的缺點，它不滿足一致風險測度的要求。滿足一致風險測度要求的有期望不足（ES）〔12〕及譜風險測度〔13～14〕，后者的表達式為

如果φ（p）=1，則得到風險價值VaR，即

如果1－α在置信水平下，小于α的部分具有等權重1/α，其余部分權重為0，則可以得到預期損失ES，即

可見，VaR、ES都是其特例。

譜風險測度φ（p）反映了風險規避的要求，需滿足以下條件：

（1）非負性：對任意的p∈（0，1〕，有 φ（p）≥0;

（3）弱遞增性：若p1＜p2，則 φ（p1）≤φ（p2）。

一致風險測度相較于其他測度模型具有明顯的主觀性特征，表現在風險規避函數φ（p）的選擇上：φ（p）不同，測度的風險大小不同。而度量風險規避的函數有多個類型，包括冪函數、指數函數、多項式函數等。但是沒有研究表明哪一個或哪一類函數更好，這也是迄今為止該模型應用中的一大困難。

跌幅風險測度相對簡單明了，但同樣具有主觀性的特征，主要體現在研究時期的選擇上，它將影響到{wτ}，進而影響到DDownt和CDaRα，另一個主觀性的體現是關于α的選擇，同VaR中的α一樣，置信水平越高，風險越大，反之亦然。

三、流動性風險測度模型及其主觀性

測度流動性風險的模型主要有兩個，一是交易成本流動性風險，即根據買賣價差確定流動性風險的大小;另一種方法是經流動性調整的VaR（LVaR）。

（一）流動性風險測度模型

1．交易成本

流動性風險可以采用交易成本來測度〔15〕。一般來說，流動性越小，買賣價差越大，反之亦然。故而，可以根據買賣價差造成的交易成本來測度流動性風險，即

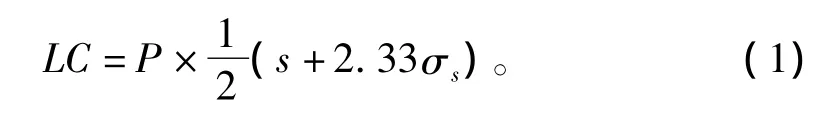
式中，P為下一個交易日資產的中間價格估計值，s為買賣價差，σs為買賣價差的樣本標準差（這里采用99%的置信水平）。

2．流動性調整的VaR

VaR是風險測度的常用指標，考慮到流動性風險對VaR進行調整，就得到經流動性調整的VaR，即LVaR，其計算式〔16〕為

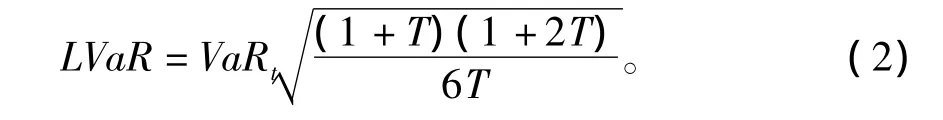
這種風險調整方法是根據單日VaR進行調整，其結果大于單日VaR，而又小于一般的VaR調整方法，如VaR，使得其更具有操作性。

除了以上方法外，也可以將交易成本考慮到VaR中，進行風險測度，前提條件是VaR是以貨幣度量〔17〕的，即

式中，LC為流動性成本，計算見式（1）。

（二）流動性風險測度模型的主觀性

從交易成本流動性風險可以看出，不同的置信水平其交易成本是不一樣的，置信水平越高，交易成本越大，風險越大，這實際反映了人們對未來損失的估計。

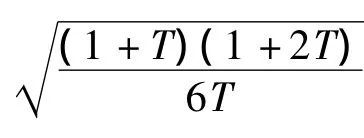
四、操作風險測度模型及其主觀性

操作風險在模型測度方面與市場風險、信用風險的主要區別在于損失事件的到達過程、損失的嚴重程度截然不同，對其測度，在建模中主要采用極值理論。

操作風險測度模型主要分為兩大類：一類是自下而上的方法，另一類是自上而下的方法。前者主要包括多因素模型、CAPM模型、操作杠桿模型等，后者主要包括過程依賴模型、精算模型和自有模型。

（一）操作風險測度模型

1．多因素模型

該模型根據多因素理論，將超額回報分解為市場風險、信用風險及其他非操作風險，剩余的殘差項 εt代表操作風險〔18〕，即

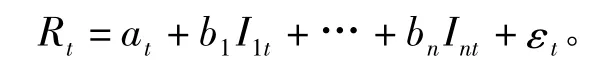
2．多因素因果模型

該模型用于操作風險的因子分析，它是操作損失對各種內部風險因素的敏感性回歸模型〔19～20〕。

式中，Xt為各種風險因子，如交易量、技術水平、產品復雜性、自動化水平、顧客滿意度等。

3．精算模型

該模型屬于一般的統計模型，模型主要涉及兩個方面，一是損失的分布，一是損失的嚴重程度。損失的分布一般服從廣義極值理論〔21～22〕。

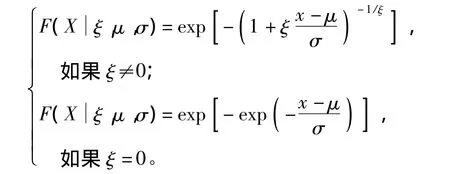
如果考慮的是超過閥值u的分布，即超過閥值的分布函數Fu（x）為

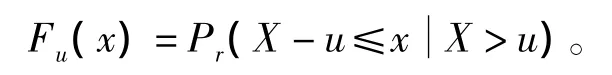
隨著u的增大，分布函數Fu（x）收斂于Pareto分布〔23〕，即

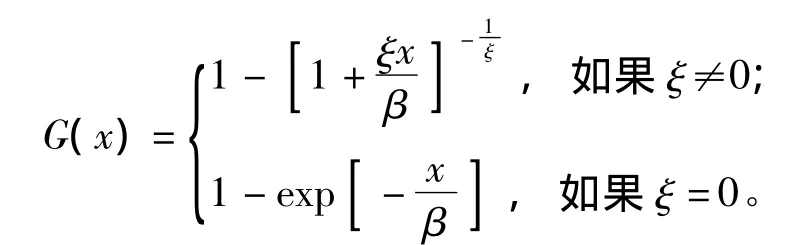
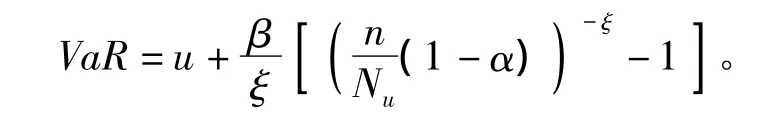
（二）操作性風險測度模型的主觀性

從以上介紹的幾個操作風險測度模型中可以看出，主觀性依然是該類模型的一個重要特征。

在多因素模型中，因素的選擇是模型的關鍵。因素選擇的越多，殘差項εt越小，即表明操作風險越小。市場風險、流動性風險、操作風險及信用風險是四種主要的風險類型，但沒有涵蓋所有的風險;以上模型是一個回歸模型，用其對未來進行預測。而未來出現新的風險類型的可能性更大，而且，金融市場風險種類眾多，風險之間并非相互獨立，一般來說，信用風險往往與市場風險相伴隨，操作風險也并非單獨出現，它可能與市場風險、信用風險同時出現，也可能造成市場風險或信用風險，也可能是它們的后果，所以模型中蘊含的主觀性更強。

由此，可以得到VaR的表達式

在多因素因果模型中，顯然風險因子的選擇是關鍵，如果選擇的風險因子比較多，將解釋大部分操作風險，而風險因子的選擇也受到因子間的關系的影響，從而為模型的解釋帶來一定的問題。

精算模型的主觀性是明顯的，除了置信水平的確定之外，閥值u的選擇具有很強的主觀性。u越大，越接近Pareto分布，但是損失的數據本身較少，如果選取較大的u，那么可得的數據就更少，因此需要在數據的可得性和良好的近似之間進行權衡，選擇合適的閥值，使得度量模型具有實用性。

五、信用風險測度模型及其主觀性

（一）信用風險測度模型

1．Merton模型

該模型是運用Black-Scholes-Merton期權定價模型來定價公司債務的信用風險〔24～26〕。

定義違約概率為

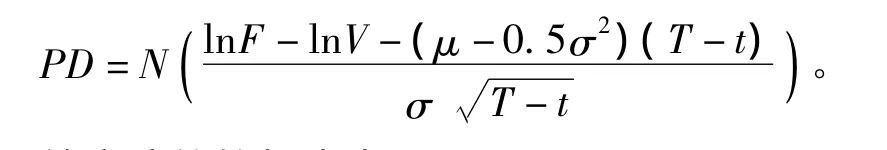
給定違約的損失為

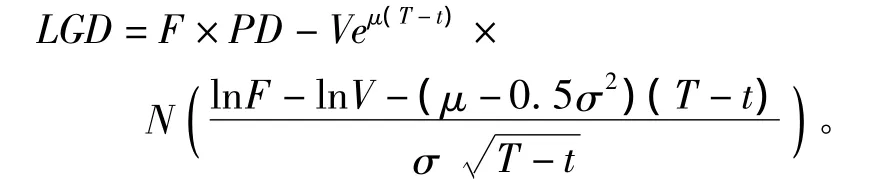
2．KMV 模型

KMV模型是對Merton模型的一個改進〔27〕，它克服了Merton模型的缺點，如Merton模型假設所有債務到期日相同，公司價值服從對數正態擴散過程。KMV模型的違約點為

違約距離

式中，EV為資產的預期價值。

3．信用評級模型

信用評級采用定性分析與定量分析相結合的方法對整個企業或個體進行評價〔28〕，這種評價方法與企業或個體的歷史信用及違約率相關性很強。一般來說評級公司將評級對象劃分為投資級別和非投資級別，前者主要包括AAA、AA、A、BBB級②，其余為非投資級別。這種評價并非一成不變的，評級公司還會給出各個級別的遷移矩陣。

運用信用評級，根據風險暴露、給定違約損失就可以計算出預期損失，即

式中，EL為預期損失，AE為調整后的風險暴露，LGD為給定違約的損失，EDF為期望違約頻率。

（二）信用風險模型測度的主觀性

Merton模型由于嚴苛的假設，使得其實用性受到限制。KMV模型是對Merton的修改，但是其違約點的確定依靠經驗法則，并沒有相應的理論依據。

信用評級主要根據企業的歷史信用，這在不同的經濟周期中是不一樣的，它不僅與企業所在行業及企業領導者有關，也與經濟發展的現實密切相關，比如在一定時期是大而不能倒的企業，在另一個時期則有可能成為倒閉企業。因此，信用評級雖然是一個信用評價模型，但是要與大的經濟環境相關聯，而且其遷移矩陣也是根據經驗確定的。

六、結論

不同的風險模型雖然反映了風險的客觀性特征，但實際上也包含了主觀的因素，這本質上就是人們對于風險的容忍度問題;在譜風險測度中，這種特征尤其明顯。在VaR及與之有關的測度中，主要體現在置信水平選擇的不同。比如對于市場風險所要求的置信水平一般為95%或99%，對于信用風險Basel協議的要求是99%，而對于操作風險的要求則為99．9%。至于其他的模型，則主觀性更強，主要是依據經驗法則來確定。風險管理的目標不是減少風險，而是股東利益的最大化，因此，我們應該認識到每一種模型的主觀性，從而對其測度的風險有一個更好的理解。

注釋：

①運行最大值（running maxima）：對于給定序列{ak}，運行最大值是指序列值{max（a1，a2，…，ak）。

②這里是S＆P的評價，Moody的投資級別是Aaa，Aa，A，Baa。

〔1〕Dowd K．Measuring Market Risk（2ndEdition）〔M〕．West Sussex，England：John Wiley＆ Sons，2005：1．

〔2〕Macaulay F．The Movements of Interest Rates，Bond Yields and Stock Prices in the United States since1856〔M〕．New York：National Bureau of Economic Research，1938：44．

〔3〕John C．Hull．Options，Futures，and Other Derivatives（8thEdition）〔M〕． Edinburgh：Pearson Education， Inc．，2012：92．

〔4〕MarkowitzH．M．PortfolioSelection〔J〕． Journalof Finance，1952，（7）：77 －91．

〔5〕Sharpe W．F．Capital Asset Prices：A Theory of Market Equilibrium under Conditions of Risk〔J〕． Journal of Finance，1964，19（3）：425－442．

〔6〕Baumol W．J．An Expected Gain Confidence Limit Criterion for Portfolio Selection〔J〕．Management Science，1963，（10）：174－182．

〔7〕Jorion P．Value-at-Risk：The New Benchmark for Managing Financial Risk（3rdEdition）〔M〕．New York：McGraw Hill，2007：106．

〔8〕Artzner P．，F．Delbaen，J．M．Eber，D．Heath．Thinking Coherently〔J〕．Risk，1997，（10）：68 －71．

〔9〕Artzner P．，F．Delbaen，J．M．Eber，D．Heath．Coherent Risk Measures〔J〕．Mathematical Finance，1999，9（3）：203－228．

〔10〕Chekhlov A，S．Uryasev，M．Zabarankin．Portfolio Optimization with Drawdown Constraints〔C〕．B．Scherer．Asset and Liability Management Tools．London：Risk Books，2003：263 －278．

〔11〕Zabarankin M．，K．Palikov，S．Uryasev．Capital Asset Pricing Model（CAPM）with Drawdown Measure〔J〕．European Journal of Operational Research，2014，234（2）：508－517．

〔12〕AcerbiC．，D．Tasche．On the Coherence of Expected Shortfall〔J〕．Journal of Banking and Finance，2002，26（7）：1487－1503．

〔13〕Acerbi C．SpectralMeasuresofRisk：ACoherent Representation of Subjective Risk Aversion〔J〕．Journal of Banking and Finance，2002，26（7）：1505 －1518．

〔14〕Acerbi C．CoherentRepresentationofSubjectiveRisk Aversion〔C〕．G．Szego．Risk Measures for21st Century．Chichester：John Wiley and Sons，Ltd．，2004：147 －207．

〔15〕Bangia A．，F．Diebold，T．Schuermann，J．Stroughair．Modeling Liquidity Risk，with Implications for Traditional Market Risk Measurement and Management〔DB/OL〕．（1998-12）［2010-11-24］．http：//fic．wharton．upenn．edu/fic/papers/99/9906．pdf．

〔16〕United States Securities and Exchange Commission．Annual Report Pursuant to Section13or15（d）of the Securities Exchange Act of1934〔DB/OL〕．（2010-12-31）〔2012-08-14〕．http：//www．goldmansachs．com/investor － relations/financials/archived/10k/docs/2010 －10 －k．pdf．

〔17〕Bangia A．，F．Diebold，T．Schuermann，J．Stroughair，Liquidity on the Outside〔J〕．Risk，1999，（12）：68 －73．

〔18〕Allen L．，T．G．Bali．Cyclicality in Catastrophic and Operation Risk Measurements〔J〕．Journal of Banking and Finance，2007，31（4）：1191－1235．

〔19〕Cruz M．Modeling，Measuring and Hedging Operational Risk〔M〕．Sussex，Engfand：John Wiley and Sons，2002：145－153．

〔20〕Haubenstock M．，The Operational Risk Management Framework〔C〕． Alexander， C．OperationRisk：Regulation，Analysis and Management．London：Prentice Hall-Financial Times，2003：241 －261．

〔21〕McNeil A．J．Calculating Quantile Risk Measures for Financial Return Series Using Extreme Value Theory．〔DB/OL〕．（1998-04）〔2013-03-26〕．http：//e － collection．library．ethz．ch/eserv/eth：25077/eth － 25077 － 01．pdf．Working Paper，Mimeo．ETHZ Zentrum，Zurich．April，1998．

〔22〕McNeil A．J．，R．Frey．Estimation of Tail-related Risk for Heteroscedastic Financial Time Series：An Extreme Value Approch〔J〕．Journal of Empirical Finance，2000，（7）：271－300．

〔23〕McNeil A．J．，T．Saladin．The Peaks Over Threshold Model for Estimating High Quantiles of Loss Data．〔DB/OL〕． （1997-04） 〔2012-07-21 〕． http：//www．financerisks．com/filedati/WP/EVT/cairns．pdf．

〔24〕Black F．，M．Scholes．The Pricing of Options and Corporate Liabilities〔J〕．Journal of Political Economy，1973，81（3）：637－659．

〔25〕Merton R．C．On the Pricing of Corporate Debt：The Risk Structure of Interest Rate〔J〕．Journal of Finance，1974，29（2）：449－470．

〔26〕Merton R．C．Pricing When Underlying Stock Returns Are Discontinuous〔J〕．Journal of Financial Economics，1976，（3）：125－144．

〔27〕Antje B．，R．Douglas，D．Duffie，M．Ferguson，D．Schranz．Measuring Default Risk Premia from Default Swap Rates and EDFs．〔DB/OL〕．（2005-02）〔2011-01-06〕．http：//www．darrellduffie．com/uploads/working/DuffieBerndtDouglasFergusonSchranz2005．pdf．

〔28〕BaselⅢ：International Convergence of Capital Measurement andCapitalStandards：ARevisedFramework-Comprehensive Version〔R〕．Basel：Basel Committee on Banking Supervision Publication，2011：52－61．