自適應神經網絡模糊小波語音消噪算法

孫燕

?

自適應神經網絡模糊小波語音消噪算法

孫燕

(青海民族大學計算機學院，青海西寧 810007)

針對有色噪聲，采用自適應神經網絡模糊系統模糊(Auto Neural Fuzzy Inference System, ANFIS)逼近有色噪聲，利用自適應神經模糊推理系統ANFIS對噪聲的非線性動態特性進行建模，提出了語音自適應神經網絡模糊小波消噪算法，建立并訓練了消噪系統。對被有色噪聲污染的測量信號經模糊消噪后，根據信號和噪聲的小波系數在不同分解尺度上的傳遞性，進行中值濾波和小波重構，得到了干凈的語音。對算法進行了仿真實驗，結果表明，消噪效果明顯。

自適應神經網絡模糊系統；小波；有色噪聲；消噪；

0 引言

信號淹沒在噪聲中，是在實際環境中經常遇到的情況，當這種噪聲為加性高斯白噪聲時，可以采用線性濾波的方法，它是最基本的減譜算法[1]，適用于對加性噪聲的消除。目前消除非加性噪聲的方法有自適應濾波如卡爾曼濾波[2]、維納濾波[3]、譜減法及其改進等，卡爾曼濾波可以在一定程度上對有色噪聲消除有效。維納濾波法對背景噪聲白化效果比較好。但對于噪聲具有非線性傳播性質時，使用線性濾波效果很差。有色噪聲可看作是白噪聲經過非線性動態處理后產生的，使用經典線性濾波的方法起不到抑制噪聲的作用。

目前語音增強的方法很多：如譜減法及改進，它是應用最早最廣泛的一種方法。它是從帶噪語音頻譜中減去噪聲頻譜分量，剩余的就是干凈語音的頻譜。其缺點是存在音樂噪聲。信號子空間法[4]是把帶噪語音分解成信號子空間和噪聲子空間上的投影，在殘余噪聲頻譜小于規定門限的情況下，使語音信號失真最小。缺點是主要針對加性寬帶高斯白噪聲。

本文利用自適應神經模糊推理系統ANFIS[5]對非線性動態特性進行建模逼近有色噪聲[6]，再利用小波變換[7]把含噪信號分解到多尺度中，然后在每一尺度下把屬于噪聲的小波系數去除，保留并增強屬于信號的小波系數，最后重構出小波消噪后的信號得到有用信號。

針對實際環境的非線性有色噪聲，本文結合經典譜減法的優點及利用自適應ANFIS對高斯白噪聲非線性動態建模逼近有色噪聲和小波閾值分解的優點，有效消除了有色噪聲，解決了經典算法對有色噪聲無效的問題。

1 ANFIS結構

1985年Takagi和Sugeno提出了一種非線性T-S模糊模型，即后來的Sugeno模糊模型[8]，是一種對有精確輸入、輸出數據集產生模糊規則推理的系統化方法。它結合模糊邏輯與神經網絡兩者之優勢，改善了傳統模糊控制設計中必須人為調整隸屬度函數以減小誤差的不足，采用混合學習算法調整前提參數和結論參數，自動產生模糊規則。后來，Tang Roger提出與一階Sugeno模糊模型功能等同的基于自適應神經網絡的模糊推理系統(ANFIS)[8,9]用來實現Sugeno模糊模型的學習過程。該網絡是一個多層前饋網絡[10,11]，結構如圖1所示。

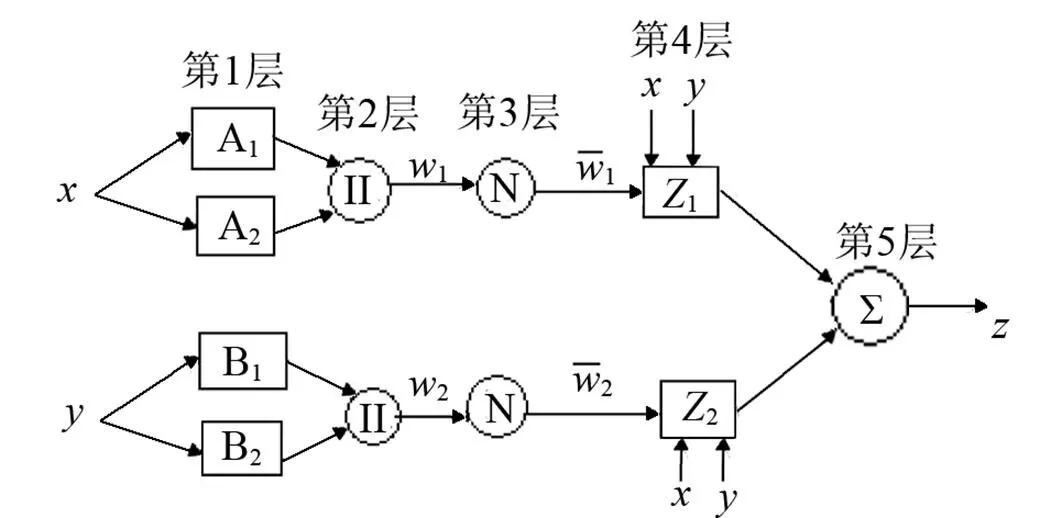
圖1 Sugeno模糊系統等效的ANFIS網絡

由圖1可見，網絡共有5層，各層功能如下：

第1層：A和B為輸入變量的模糊子集，該層節點的激活函數代表模糊變量的隸屬函數，該層的輸出代表模糊化結果，即隸屬度，其中一個節點的傳遞函數可以表示為：

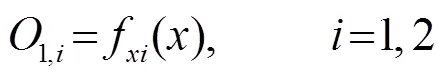
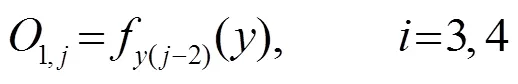
第2層：將模糊化得到的隸屬度兩兩相乘，該層的輸出代表著模糊規則的強度或適用度。

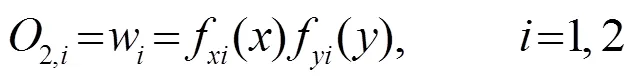
其中用表示上一層的隸屬度。

第3層：將各條規則的適用度歸一化：

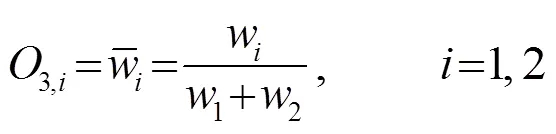
第4層：計算每條規則的結論：

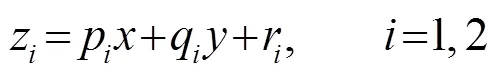
第5層：計算所有規則的輸出之和，即系統輸出：

2 自適應神經網絡模糊小波消噪原理

自適應神經網絡[12]模糊小波消噪原理見圖2。

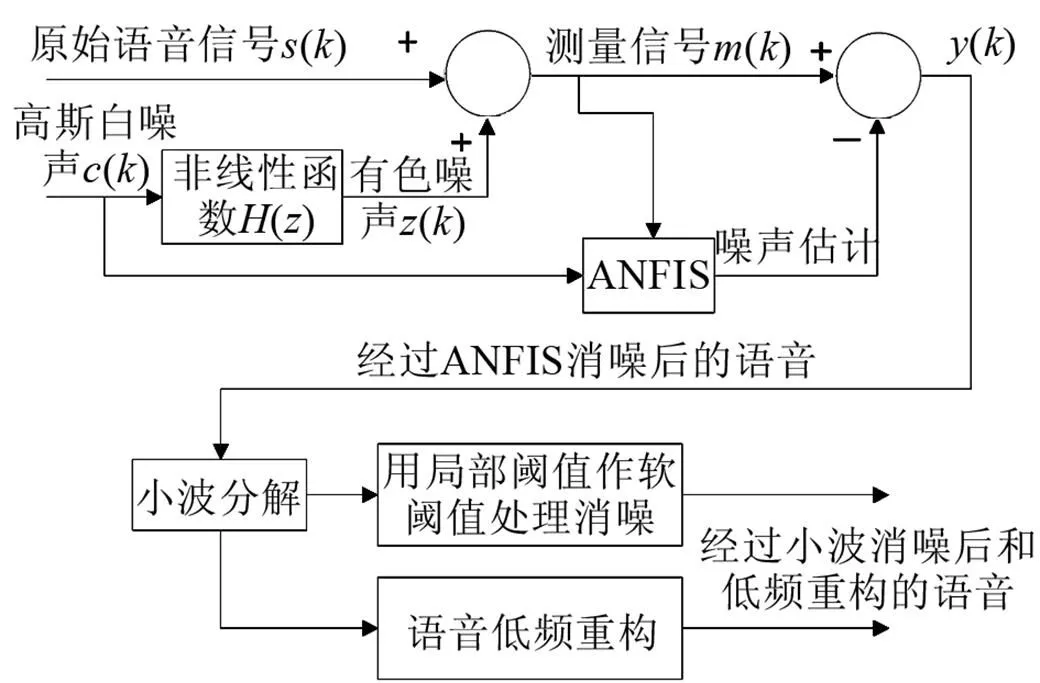
圖2 語音自適應神經網絡模糊小波消噪原理

自適應神經網絡模糊小波消噪是將高斯白噪聲與其延遲和測量信號作為系統訓練集，通過ANFIS系統模糊逼近測量信號中的有色噪聲，從被有色噪聲污染的測量信號中減去逼近的噪聲，再經過小波的低通濾波將高頻噪聲濾除得到干凈的語音信號。

2.1 ANFIS噪聲估計

有色噪聲為白噪聲通過下列非線性函數后產生：

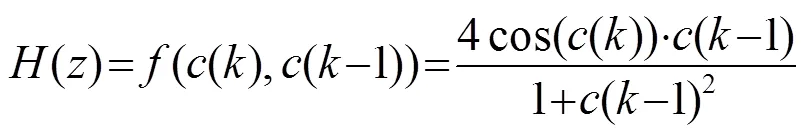
仿真實驗非線性函數特性曲線就是由這個函數構造得出的，如圖4所示。

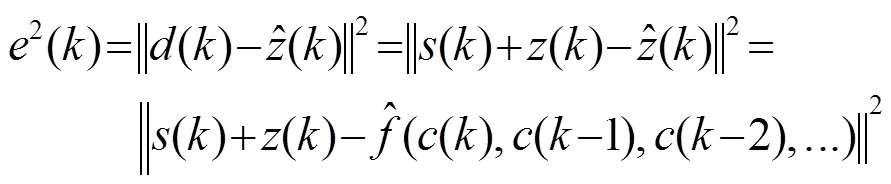
將式(7)展開，得到

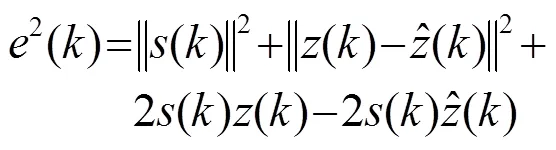
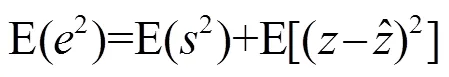
2.2 小波閾值

小波消噪原理是將含噪信號在各尺度上進行小波分解，設定一個閾值，幅值低于該閾值的小波系數置為0，高于該閾值的小波系數或者完全保留，最后將處理后獲得的小波系數用逆小波變換進行重構，得到去噪后的信號。閾值去噪中，閾值函數體現了對超過和低于閾值的小波系數不同處理策略，是閾值去噪中關鍵的一步。

設表示小波系數，為給定閾值，sgn(.)為符號函數，常見的閾值函數有：

硬閾值函數：

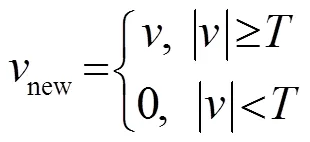
軟閾值函數：

3 算法仿真實驗

在實驗室環境下錄制語音文件。所錄語音為8 kHz采樣率、8 bit量化、線性PCM編碼的數字語音；實驗仿真結果如圖3~10所示。圖3是原始語音及頻譜。圖4是非線性函數的特性曲線，由式(6)構造得出。圖5是測量語音信號與頻譜，從圖5中根本無法看出任何的語音信息。圖6是有色噪聲的估計，其頻率范圍與測量信號頻率范圍重疊。圖7是經過非線性變換后的噪聲信號和頻譜。從圖8可以看出被有色噪聲污染的測量信號經過ANFIS系統消噪后，可明顯分辨出語音信號。圖9是經過小波消噪后的語音，消噪效果進一步優化。圖10是被有色噪聲污染后經過維納濾波消噪后的語音，可見消噪效果不好，基本得不到語音信號，語音信號還是被淹沒在噪聲中。從圖8、9與圖10的對比可見，其中信噪比為=50，采用自適應神經網絡模糊信號和小波消噪算法對于去除有色噪聲是有效的。圖11是上述方法在=3時的比較，雖然從波形上還是有噪聲，但是播放時得到清晰可辨的語音，可見該算法在低信噪比下也是有效的。

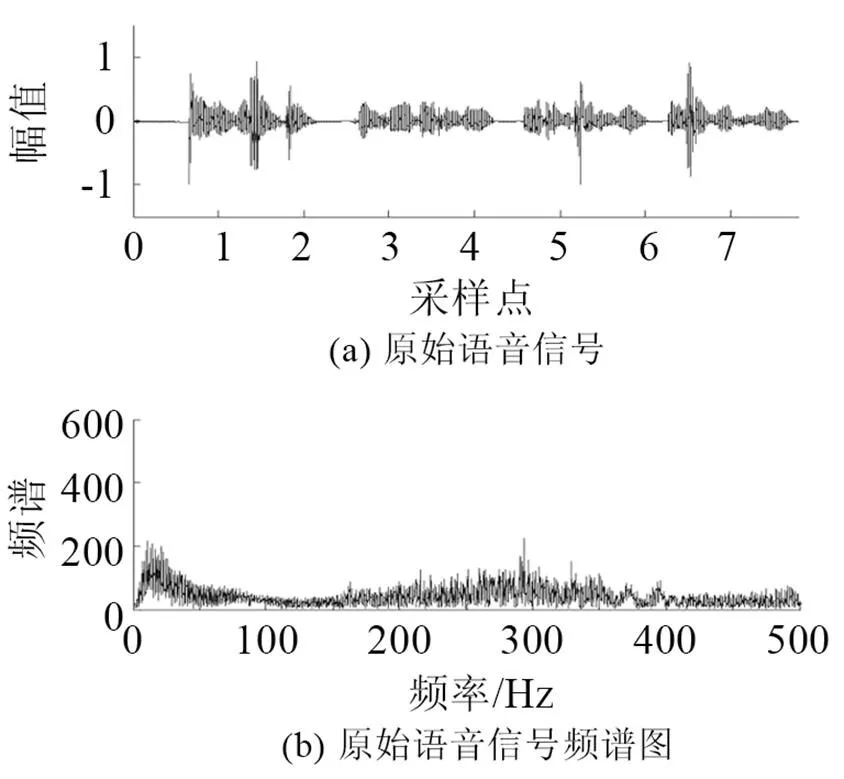
圖3 原始語音及頻譜

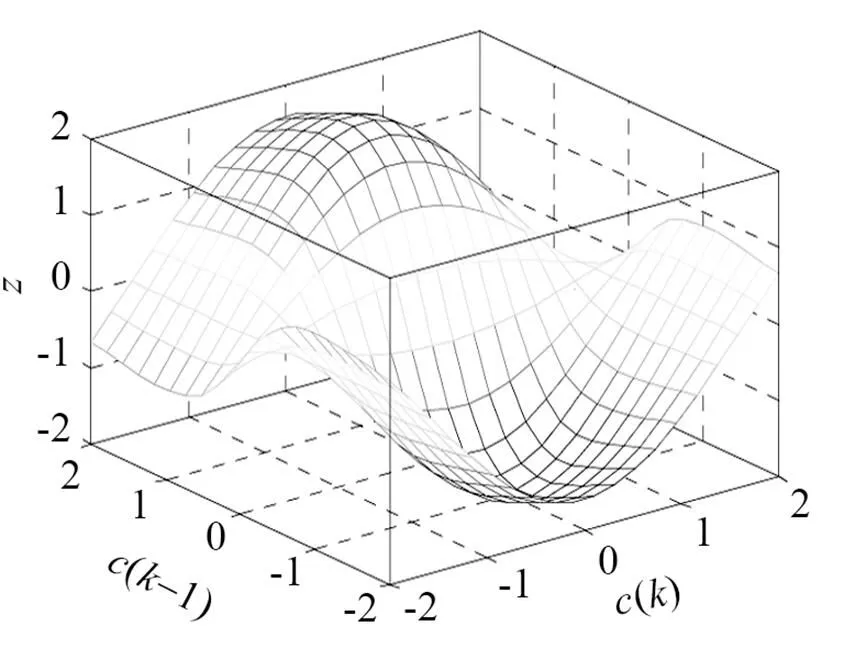
圖4 特性曲線

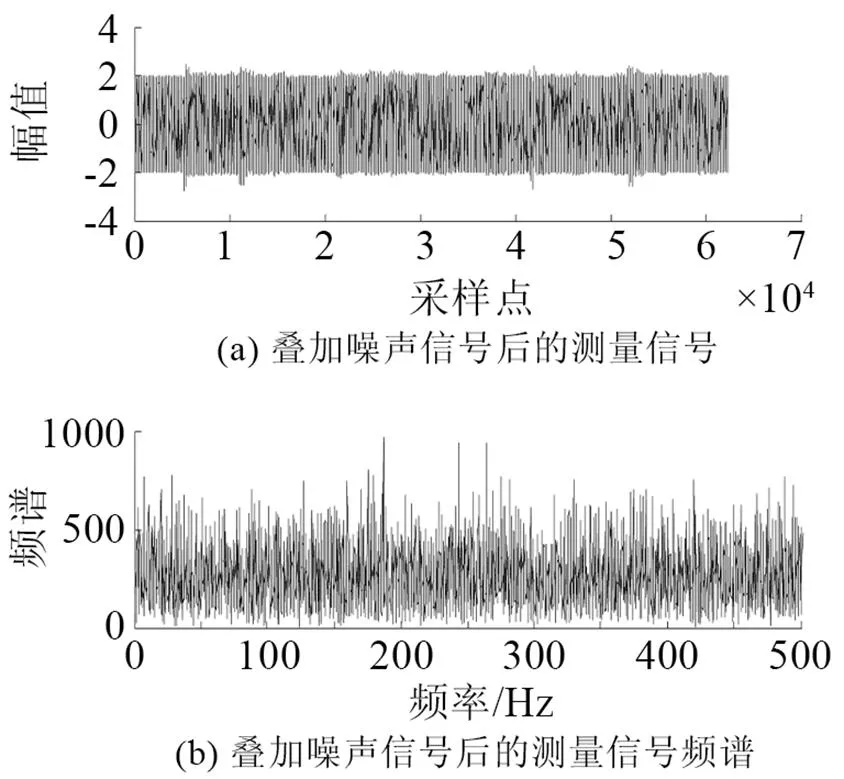
圖5 疊加有色噪聲的測量語音信號與頻譜

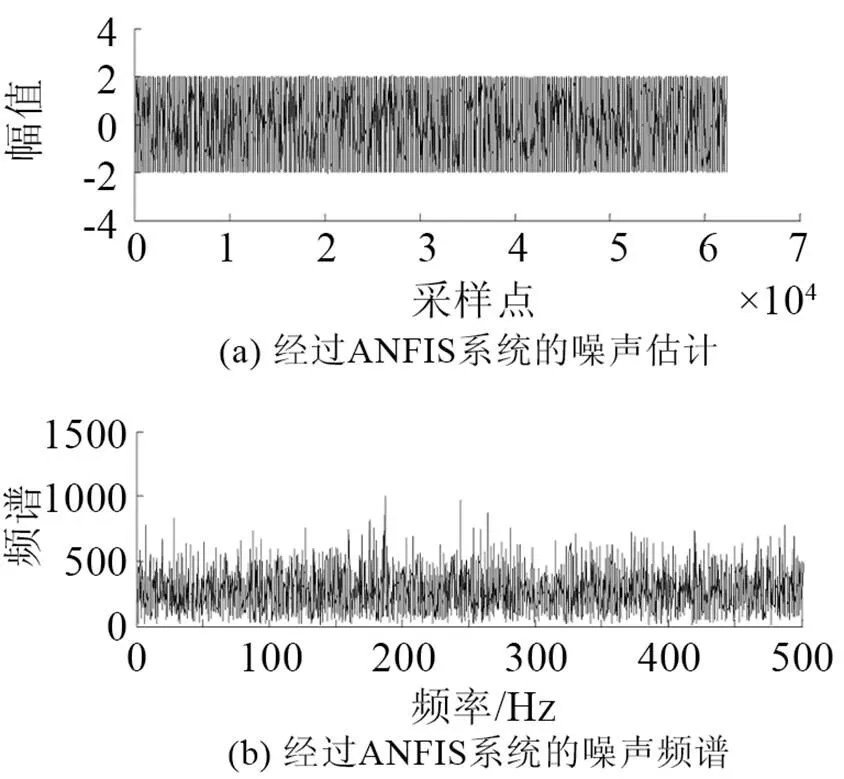
圖6 經過ANFIS系統的噪聲估計與頻譜

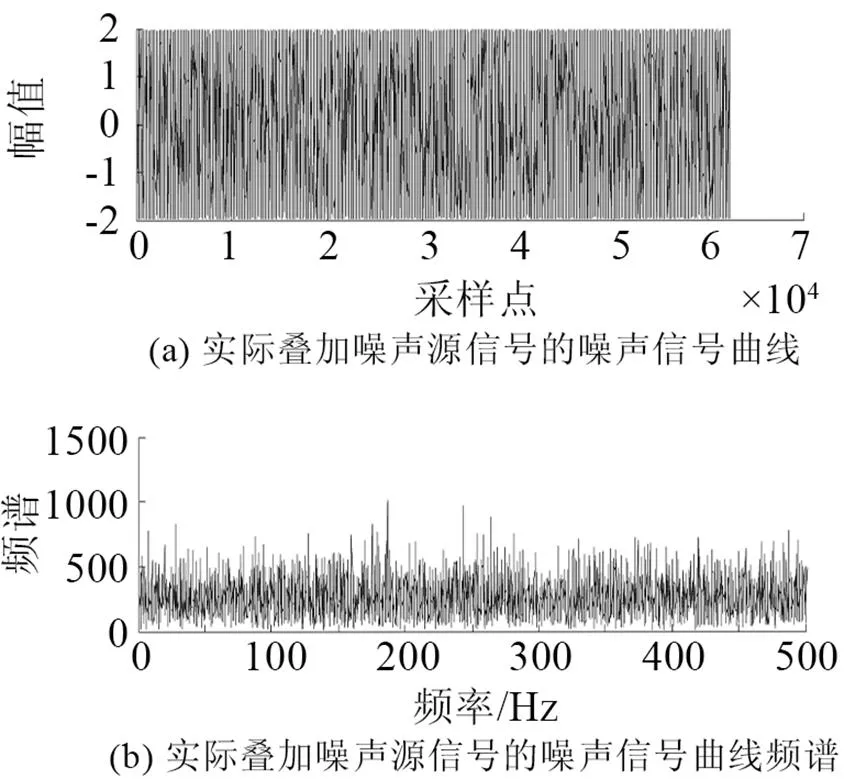
圖7 經過非線性變換后的噪聲與頻譜

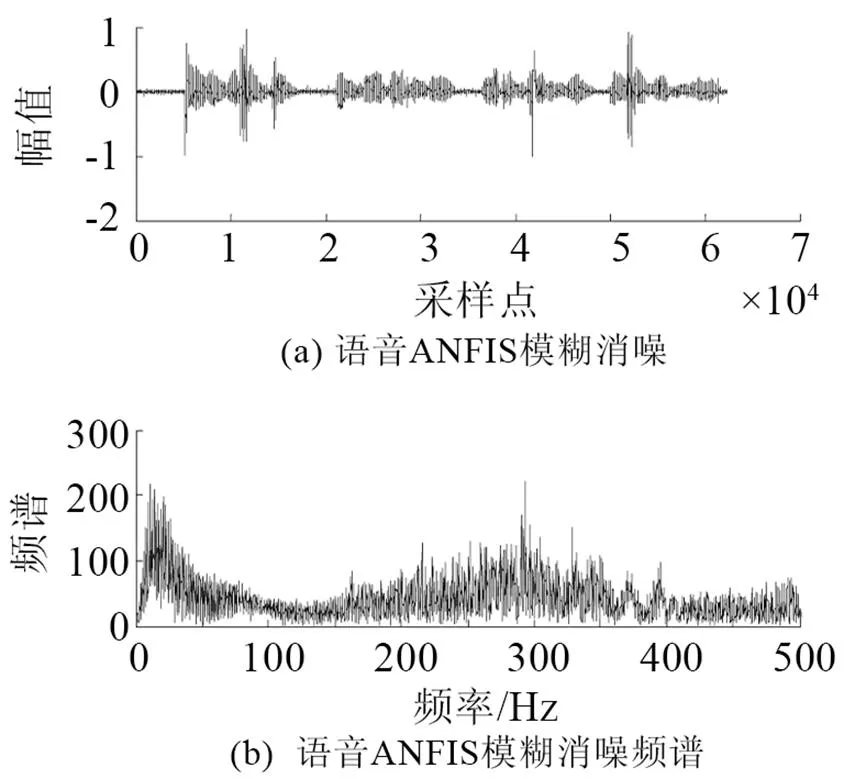
圖8 經過ANFIS消噪后語音與頻譜 SNR=50

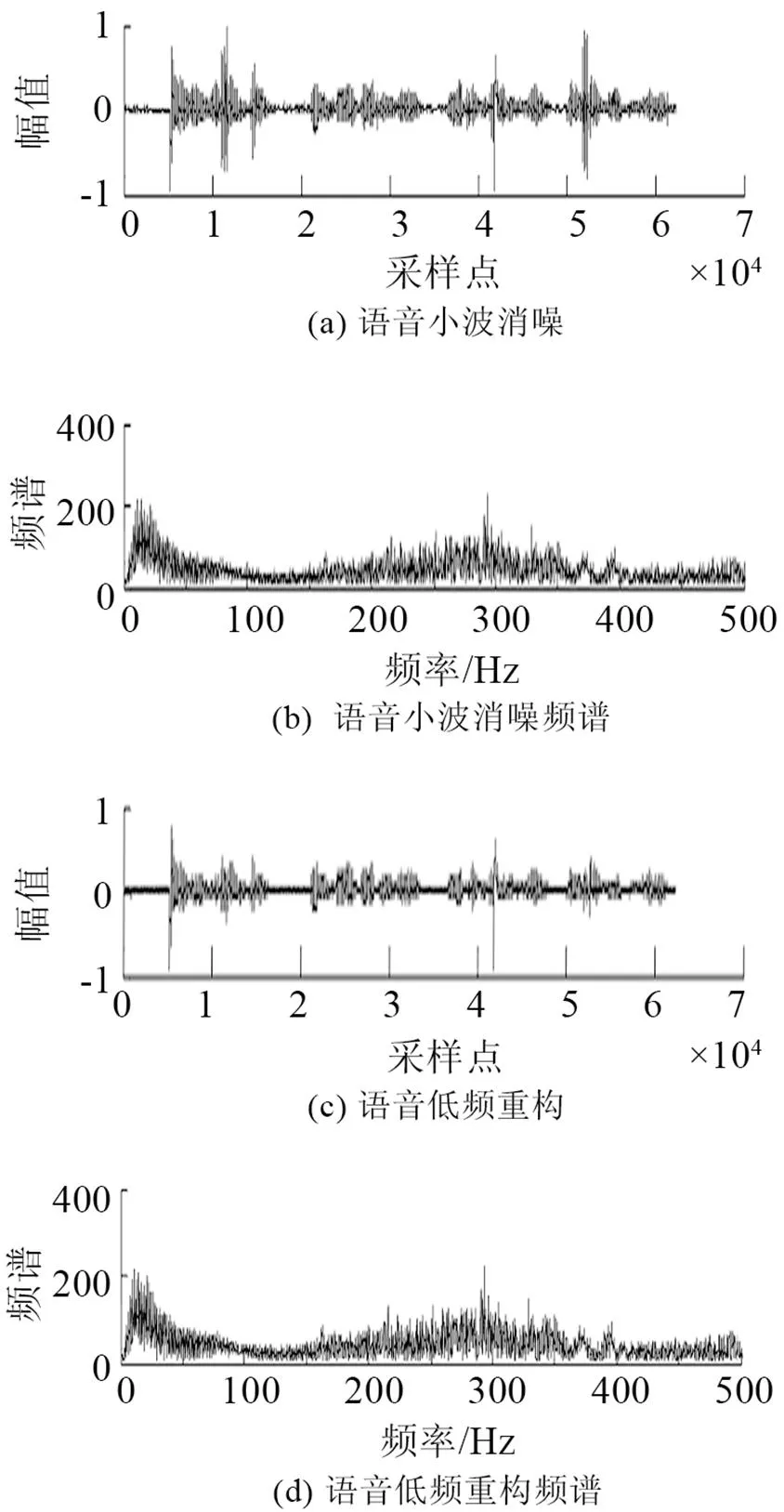
圖9 語音小波消噪和低頻重構及頻譜SNR=50

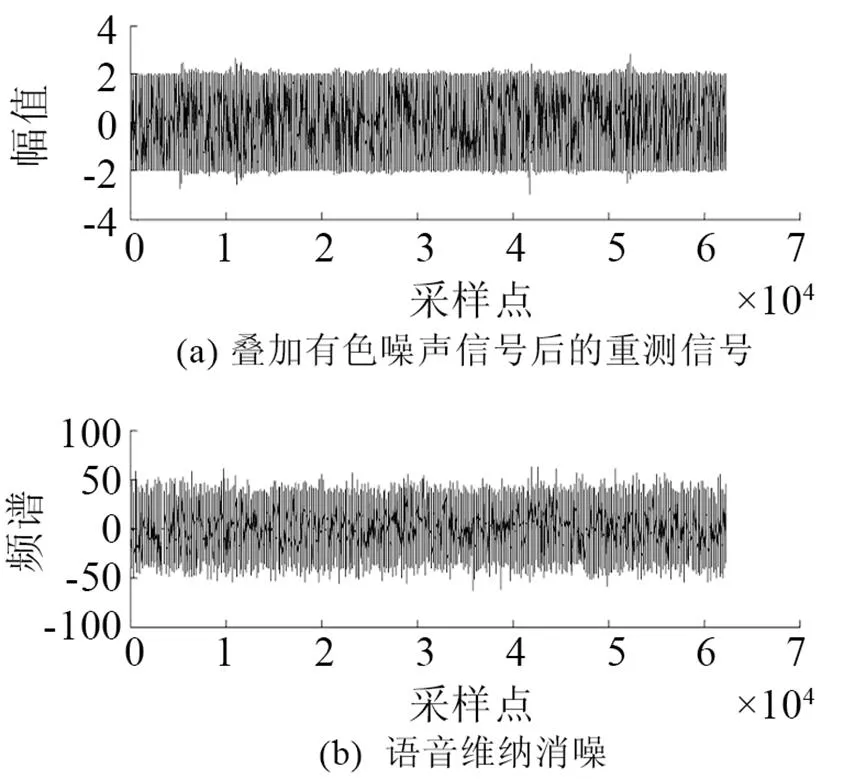
圖10 語音維納消噪

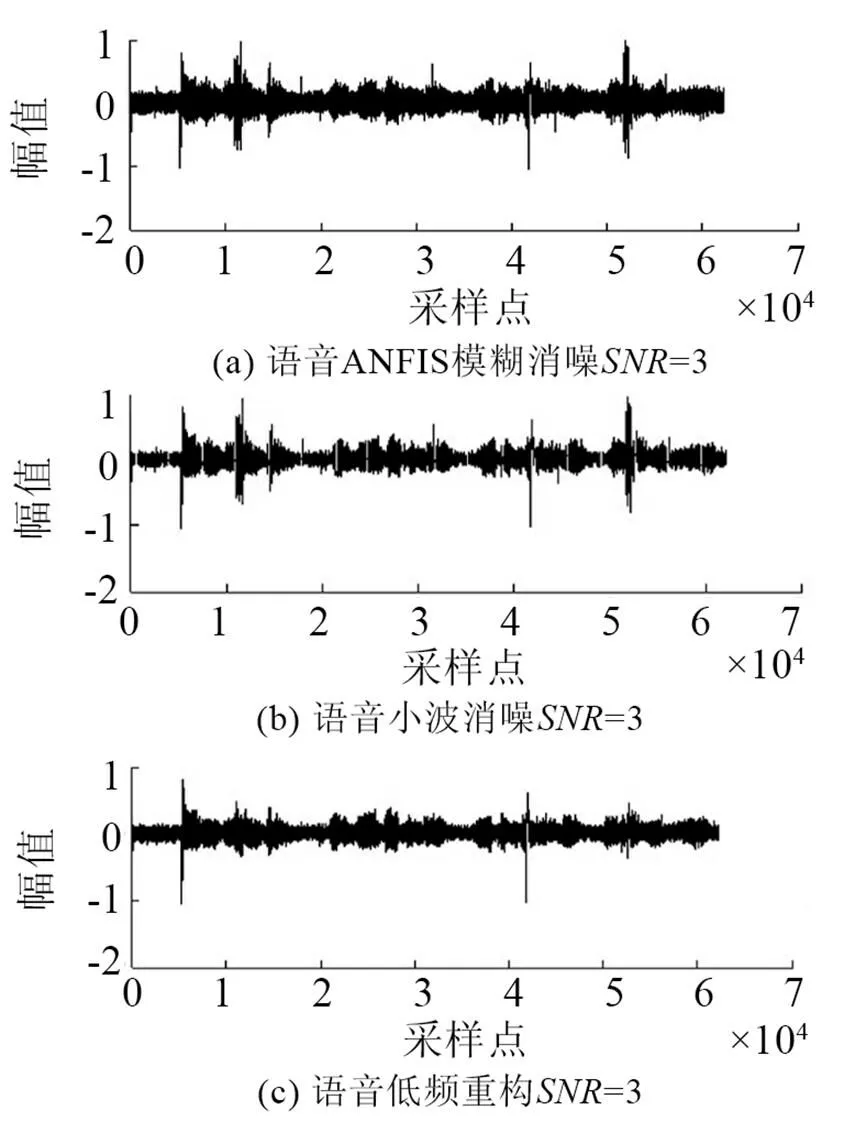
圖11 SNR=3 ANFIS消噪后語音和小波消躁及低頻重構語音波形

4 結論

自適應神經網絡模糊小波語音消噪算法，可在未知外界干擾源特征、傳遞途徑不斷變化以及背景噪聲和被測對象相似的情況下，能夠有效地消除外界有色聲源的干擾，獲得高信噪比的語音信號，這一算法為在測試環境不太理想的工作現場做測試分析和故障診斷時，提供可靠的方法和依據。

[1] 趙曉群. 數字語音編碼[M]. 北京: 機械工業出版社, 2007.

ZHAO xiaoqun, Digital speech coding[M]. Beijing: Mechanical Industry Publishing Press, 2007.

[2] PALIWAL K, BASU A. A speech enhancement method based on Kalman filtering[C]// Proc Acoustics Speech and Signal Processing, IEEE International Conference on IC A SSP' 87.[S.l.]: IEE E Press,1987, (12): 177- 180.

[3] Wiener, Norbert. Extrapolation, interpolation, and smoothing of stationary time Series[M]. New York: Wiley.

[4]signalapproach for speech enhancement[J]. IEEE Transactions on Speech and Audio Processing, 1995, 3(4): 251-66.

[5] Staib W E, Bliss N G, Staib R B. Recent developments in neural network applications - neural network conversion of the electric arc furnace into the intelligent arc furnace[C]// 1991 AISE Spring Conference, 1991.

[6] 崔先強, 楊元喜, 高為廣. 多種有色噪聲自適應算法的比較[J]. 武漢大學學報: 信息科 學版, 2006, 31(8): 731-735.

CUI Xianqiang YANG Yuanxi GAO Weiguang. A variety of colored noise adaptive algorithm is compared[J]. Journal of Wuhan University Information: Science Edition, 2006, 31(8): 731-735.

[7] 郭桂容. 模糊模式識別[M]. 長沙: 國防科技大學出版社.

GUO Guirong. Fuzzy pattern recognition[M]. Changsha: National University of Defense Technology Press.

[8] 張毅, 楊秀霞. 小波消噪在微弱信號檢測中的應用[J]. 微計算機信息, 2006, 1(1): 113- 114.

ZHANG Yi,YANG Xiuxia. Wavelet denoising in the application of weak signal detection[J]. Journal of Micro Computer Information, 2006, 1(1): 113-114.

[9] 張乃堯, 閻平凡. 神經網絡與模糊控制[M]. 北京: 清華大學出版社, 1998.

ZHANG Naiyao, Yan Pingfan. Neural network and fuzzy control [M]. Beijing: Tsinghua University Press, 1998.

[10] Widrow B. Glover J R, Mecool J, et al.Adaptive noise canceling: principles and application[J]. Proc IEEE, 1975, 63(12): 1692-1716.

[11] 樓順天, 胡昌華, 張偉. 基于MATLAB的系統分析與設計---模糊系統[M]. 西安: 西安電 子科技大學出版社, 2005.

LOU Shuntian, HU Changhua, ZHANG wei. Based on the MATLAB system analysis and design - fuzzy system[M]. Xian Xi’an: University of Electronic Science and Technology Press, 2005.

[12] Staib W E, Bliss N G, Staib R B. Neural network conversion of the electric arc furnace into the intelligent arc furnace[C]// 74th AIME Steelmaking Conference, 1991.

Algorithm for ANFIS and wavelet denoising of speech signal

SUN Yan

(Computer Department of Qinghai University for Nationalities, Xi’ning 810007,Qinghai, China)

An ANFIS and wavelet denoising algorithm is proposed for additive colored noise. Modeling the nonlinear dynamic characteristic of noise by ANFIS and fuzzy approximating colored noise, the Auto Neural Fuzzy Inference System (ANFIS) and wavelet denoising system of speech signal is set up and trained. According to the different wavelet coefficients’ transmission properties of edge signals and noises under the different scales of the wavelet transform, the median filter is designed. Colored noise can be successfully removed by using subtraction in the original speech signal. Experimental results show that the algorithm is effective.

Auto Neural Fuzzy Inference System(ANFIS); wavelet; colored noise; denoising

TN912.35

A

1000-3630(2014)-03-232-05

10.3969/j.issn1000-3630.2014.03.010

2013-02-01;

2013-05-12

孫燕(1973－), 女, 山東青島人, 副教授, 碩士, 研究方向為語音 處理和語音編碼。

孫燕, E-mail: 453856400@qq.com