一類非線性系統的主動同步仿真

楊　　宸

（中國礦業大學（北京）理學院，北京　100083）

一類非線性系統的主動同步仿真

楊宸

（中國礦業大學（北京）理學院，北京100083）

摘要：近年來隨著混沌理論的不斷發展，混沌現象在各個領域都具有廣泛應用，其中混沌同步控制是混沌理論研究的重要內容。本文利用主動控制同步的方法對一類分數階系統進行了同步實驗，仿真結果證明了該方法的有效性和可行性。

關鍵詞：分數階；非線性系統；同步

1　引言

為了解決P-C同步的局限性，L.Kocarev和V.Par1itoz于1995年對P-C同步進行了改進，提出了主動--被動同步法。與P-C同步法相比主動--被動同步法的優勢在于可以不受限制的選取驅動變量，采用較靈活的普適的分解法，更適合于混沌同步和超混沌同步。本文中以所給出的分數階非線性系統為例，嘗試了主動控制法［1]同步控制，仿真結果證明了主動控制法的有效性和可行性。

2　基于主動控制法的同步

驅動系統可以寫為：

為常數矩陣，u為主動控制函數。

記誤差為：e=y-x，誤差系統可以寫為：

（1）驅動系統為：

設計響應系統為：

將主動控制函數u代入響應系統（2.5）得

將主動控制函數u代入誤差系統（2.6）得

由分數階系統穩定性判定引理，可知。

此時響應系統與驅動系統同步。

（2）仿真分析

利用matlab2010a進行數值仿真，仿真時間設為［0，200]，仿真初值設為

（a，b，c）=（0.9，0.2，1，2），誤差系統初值為［-8，5.5，5.5]。

此時出現混沌現象，這里N=5000，h=0.04，得到下面的仿真圖形。

圖2.1　系統x1與系統y1比較

圖2.2　系統x2與系統y2比較

圖2.3　系統x3與系統y3比較

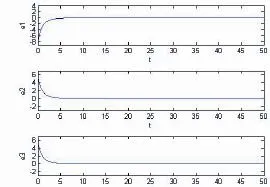
圖2.4　誤差曲線

3　結論

本文將反饋同步的思想引入到分數階系統同步控制理論中，對文中所給出的系統采用非線性方法進行了完全同步，仿真結果證明了反饋同步方法的可行性和有效性。

參考文獻：

［1]Sachin Bhalekar，Varsha Daf tardar-Gej j i.Synchronization of di f ferent f ractional order chaotic systems using active cont rol［J]，Commun Nonl inear Sci Numer Simulat，2010，15（2010）3536-3546

［2]孟令博.分數階混沌系統的同步控制方法研究［D]，江蘇南京：南京理工大學，2010

［3]宋銀芳.一類金融混沌系統的控制設計［D]，湖北武漢：華中科技大學，2006

作者簡介：楊宸，男，在讀碩士研究生，中國礦業大學（北京）理學院，研究方向為復動力系統。