基于G-K模糊聚類的故障診斷方法研究

鄭慶利

(中國人民解放軍91604部隊，山東 龍口 265700)

0 引言

近年來，隨著故障診斷技術理論研究的不斷深入，各種方法相互滲透借鑒，目前該領域我國在大系統故障診斷、多元統計分析、基于信息融合方法、基于神經網絡的方法、基于專家系統方法等方面取得了一系列的研究成果，其中部分領域處于國際領先地位[1-2]。盡管故障診斷技術的相關研究不斷深入，取得了很多成果，但工業技術的整體進步迅猛，使得故障診斷技術理論及應用研究都急需加強。目前該領域的研究熱點問題有[3]：復雜系統多故障檢測；基于人工智能的故障推理機制；多信息融合故障診斷方法；強擾動系統故障診斷；實用化工程故障診斷軟件的開發。

聚類分析是近二十年發展起來的一種新的數學方法，聚類就是將一個數據集劃分為若干組或類的過程并使同一組內的對象具有較高相似度，而不同組的對象之間相似度較差，組內對象之間的相似度越高而不同組對象之間的差別程度越大，聚類的質量也就越高。故障診斷領域應用最多的是基于模糊理論衍化的各種模糊聚類分析方法[4]，因為對故障的識別問題往往伴有模糊性，即需要確定的不僅是定性的有或者無，更重要的是相識程度，這些問題用模糊語言來表達更為自然和符合實際。

1 模糊聚類故障診斷模型

Gustafson-Kessel(G-K)算法是距離自適應動態聚類算法的模糊推廣，可以用于搜索橢圓型、平面和線型的數據模式的聚類。G-K算法在模糊模型的識別中對數據類的幾何結構特征刻劃要好于其他算法。

G-K算法中，定義vi為第i個原型類的中心，Mi為與第i個聚類中心的協方差矩陣Fi相關的正定對稱矩陣，n為輸入輸出成績空間的維數。則點xj到聚類Ci的距離可以定義為

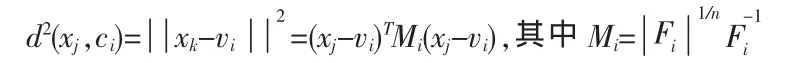
設U=[uik]為待進行處理的數據集X{x1，x2…，xN}的模糊劃分矩陣，則將X劃分成c個模糊類別的最小化目標函數可以表示為

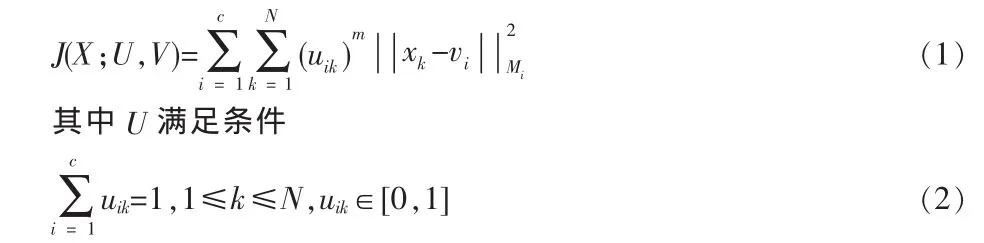
m∈(1，∞)為模糊指數，決定著所得分類的模糊程度(對于清晰模型，m=l；模糊模型m＞1，大多數情況下取 m=2)。 Lagrange乘子 λk可以將上述目標函數及其約束轉化成新的目標函數

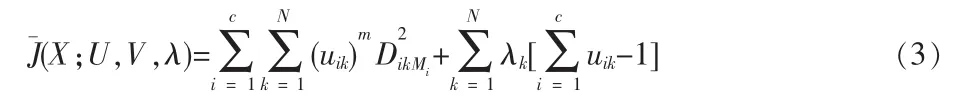
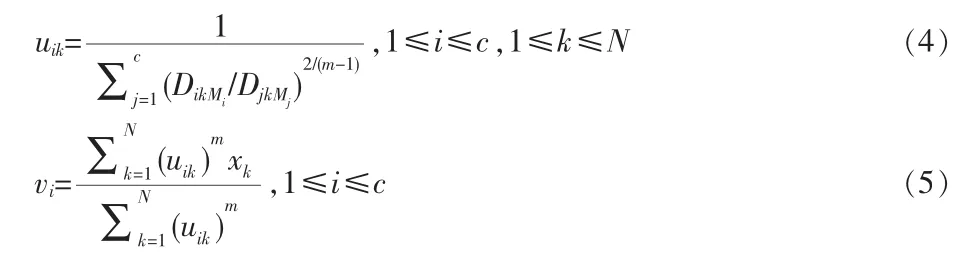
在某種程度上，第i類的形狀可以用下述的散點矩陣來描述

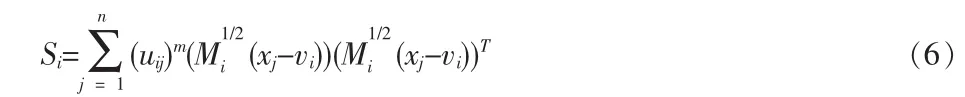
如果數據集圍繞中心點形成橢圓形聚類，那么橢圓的主軸將由Si的特征向量近似給出，而軸的相對長度等于其特征值。由于G-K算法使用了各模式類Ci的模糊協方差矩陣Fi的估計信息，而Fi的特征結構能夠提供其相應模糊類Ci的形狀和方向信息，因此G-K模糊聚類能夠在同一個數據集中識別出不同形狀和方向的模糊模式類，對數據集中的模式類原型具有一定的自適應性。

G-K算法可以表述如下[5]。

給定一組數據 X{xj｜j=1，2，…，N}，首先假定聚類中心為 vi，協方差矩陣為Fi，模糊劃區矩陣為U=[uij]，迭代執行以下步驟

1）計算距離

如果對某些 i=k，存在 d2(xj，Ci)=0，則令 ukj=1，而且?i≠k，uij=0

3）計算新的聚類中心

使用G-K算法對數據集X進行聚類，實際上是對輸入數據空間進行與數據集中的原型相適合的、隨數據集的變化而精細可調的“軟”劃分，原來的數據集被分成了一組模糊類Ci(1≤i≤c)，其聚類中心為vi(1≤i≤c)，模糊劃分矩陣為 U=[uik](1≤i≤c，1≤k≤N)。

2 基于G-K模糊聚類的故障診斷模型

當將G-K模糊聚類用于輸入輸出乘積空間的故障數據時，相應于不同質量的故障診斷模型，一些特有的聚類結果就產生出來。

假設x∈Rn是輸入數據向量，y∈R是故障類別，即輸出數據為整數。記Zk=[，yk]T，k表示第k個數據點，定義模糊聚類Ci的類型為相應聚類中心 Vi=[vi1，vi2，…，vi，n+1]T類型分量 vi，n+1。

命題1 高質量的故障診斷模型意味著每一個聚類具有很高的分類精度，這在聚類結果中直觀地表現為類Ci的幾乎所有的數據點的類別值是相等的，而且它們幾乎等于聚類中心Vi=[vi1，vi2，…，vin]T的類型分量 vi，n+1，即 vi，n+1=yik。 這樣聚類 Ci的模糊協方差矩陣 Fi具有下面的形式

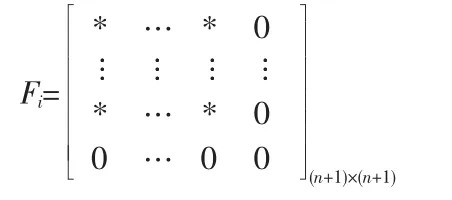
Fi的最后一行和最后一列對應著聚類Ci的類型。上式表明：

1）故障類別變量y與其它數據點的協方差近似為零，即cov(x,y)=0；

2）聚類Ci的故障類別變量夕的方差近似為零，即

D(vi，n+1)=cov(y，y)=Fi(n+1，n+1)≈0

那么，聚類Ci(1≤i≤c)的高斯隸屬函數是一些窄脈沖，它們的中心等于聚類中心的類型分量vi，n+1，如下圖1所示。

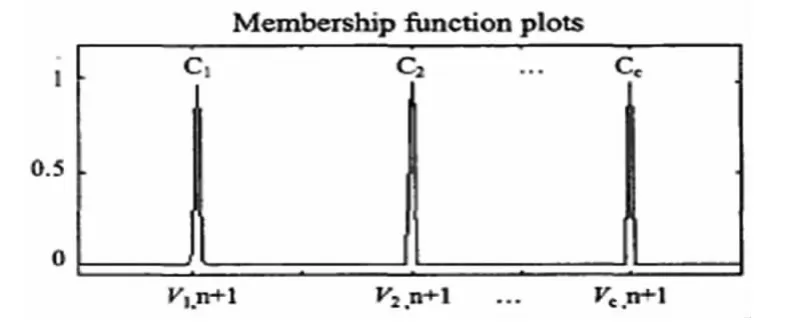
圖1 高質量故障診斷模型類Ci中的類型vi，n+1隸屬函數

命題2低質量的故障診斷模型意味著大部分聚類的分類精度是很低的，在聚類的結果中表現為大多數聚類Ci的數據點的類別值具有很大的差異，而且，它們遠遠偏離聚類中心Vi=[vi1，vi2，…，vin]T的類型分量 vi，n+1。 這 表 明：

1）故障類別變量y與其它數據點的協方差通常為非零值，即cov(x,y)＞0；

2）聚類Ci的故障類別變量的方差是一大的數值，即，

D(vi，n+1)=cov(y，y)=Fi(n+1，n+1)＞0

因此，相應于低質量的故障診斷模型，其聚類的高斯隸屬函數具有一些平坦的

曲線，它們的中心偏離于它們真實的類別值，如圖2所示。

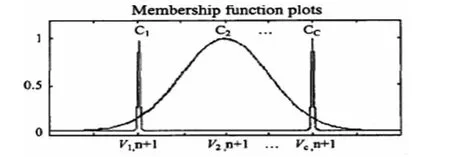
圖2 低質量故障診斷模型類Ci中的類型vi，n+1隸屬函數

由此這樣在乘積空間中使用G-K算法進行聚類后，我們實際上獲得了一組模糊類Ci(i=1，2，…，C)在以上的模型中，對積空間中C個聚類中心的方差D(vn+1)設立了一個容差向量，tolSig2＞0，∈RC，其中C是類數量。只有所有聚類中心的方差都滿足

D(vi，n+1)＜tolSig2(i)(i=1，2，…，C)

的聚類結果才被接受用來建立故障診斷模型；否則,增加聚類數目C，再一次執行模糊聚類算法。

3 G-K模糊聚類故障診斷方法

模糊聚類Ci在輸入空間中可以用它的中心向量[vi1，vi2，…，vin]和方差向量[]來表征。如果對每一個聚類分量指定一個高斯型隸屬函數

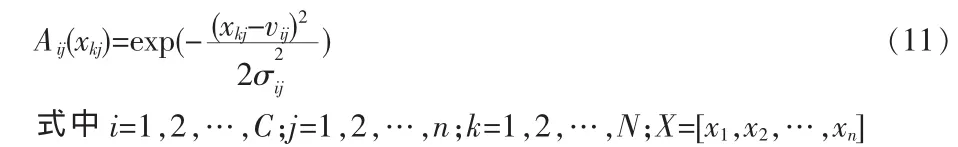
這些隸屬函數可以通過將聚類Ci投射到它的每一維上獲得，那么可以得到一組模糊故障診斷規則，規則中的每一個前件命題表示成單變量模糊集命題的邏輯組合，單變量模糊集是針對X的各個分量定義的，并且通常以下面邏輯與的形式給出

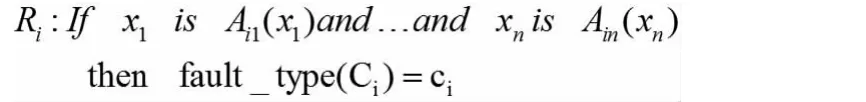
在這種情況下，數據xk相對于故障聚類Ci的故障度DoFi(xk)可被定義為投射空間中各隸屬度的乘積

而在笛卡爾乘積空間中，DoFi(xk)可以被簡單地定義為多維模糊集Ci的隸屬度

總結以上可以得出以下結論：

對于任意數據 Data(i)，如果{DoFj(Data(i))≥TH(j)，(j=1，2，…，C)}（TH為預先定義的一個常數閥值向量），那么Data(i)∈Cj；否則Data(i)?Cj。 通過 DoFj(Data(i))j=1，2，…，C，數據樣本 Data(i)的最終類型綜合為下面的兩種情況：

1）存在一個或多個 DoFj(Data(i))，使

DoFj(Data(i))≥TH(j)，j=1，2，…，C

這種情況下，如果所有聚類規則的后件值(即聚類中心的vi，n+1和分量)都相等或近似相等 那么取具有最大DoF(Data(i))值的聚類，j作為數據Data(i)所屬的類；否則，數據Data(i)就被看成是無法識別的數據點。

2）不存在 DoFj(Data(i))，使得

DoFj(Data(i))≥TH(j)，j=1，2，…，C

這意味著沒有檢測到故障，系統工作狀態正常。

4 實例分析

采用某裝置電源系統的故障診斷進行本文算法的仿真研究。表1為由故障仿真平臺產生的測量數據集，共15組采樣數據，最后一列是故障類型：1-能量衰減故障，2-線性分路電流控制器故障，3-無故障。

表1 電源系統故障診斷的數據集

對該數據集選擇屬性Icna和Icnb建立故障診斷模型，得到7個故障模式類，如表2所示。于是，根據表2，獲得電源系統的故障診斷規則如下：

當設定tolV=0.01及tolSig2=0.01時，上述模糊故障診斷模型對訓練數據表1的識別精度達到100%。由故障仿真平臺另外產生15組數據樣本作為測試數據集，所獲得的故障診斷模型的有效識別精度可達93.3%，實驗結果表明該方法是有效的。

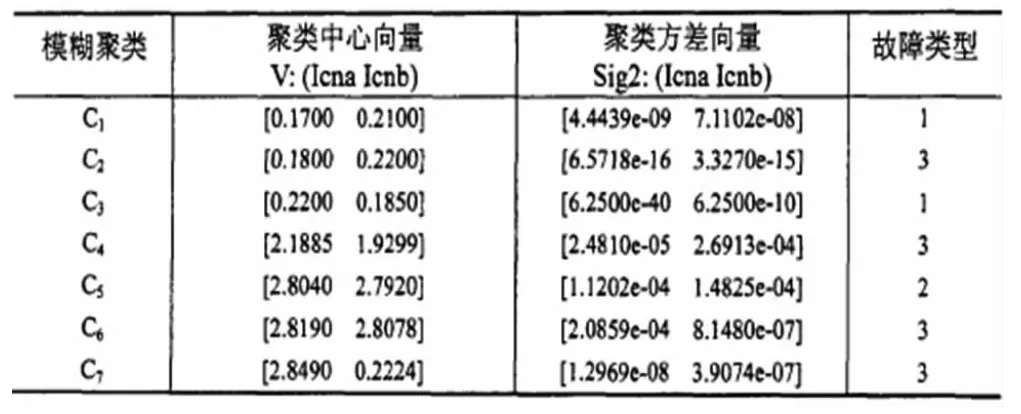
表2 用于故障診斷模型的模糊聚類

5 結束語

利用G-K算法提出了一種在輸入輸出乘積空間中，通過模糊聚類獲得基于知識的故障診斷模型的方法。該方法可以發現數據集中不同形狀和方向的故障模式，同時該方法比傳統的故障診斷模型更具柔性，具有更強的處理噪聲數據的能力。

［1］周東華.國內動態系統故障診斷技術的一些最新進展[J].自動化博覽，2007(10)：16-18.

［2］于春梅，楊勝波，陳馨.多元統計方法在故障診斷中的應用綜述[J].計算機工程與應用，2007，43(8)：205-208.

［3］BO-SUK YANG,XIAO DI,TIAN HAN,Random forests classifier for machine fault diagnosis[J].Journal of Mechanical Science and Technology,2013,22(9)：16-25.

［4］高新波.模糊聚類分析及其應用[M].西安：西安電子科技大學出版社，2004：2-40.

［5］杜運成，石紅瑞，楊曉波.控制系統故障診斷方法綜述[J].工業儀表與自動化裝置，2008(5)：9-13.

［6］Lv Ning,Qiao Yu-jing,Yu Xiao-yang,et al.Building of fault diagnosis model based on Custafson-Kessel fuzzy clustering.Harbin Institute Technology Publishers[C]//Proceedings of the 3th International Symposium on Instrumentation Science and Technology,2004,1：511-516.