橋梁式高架車站的固有頻率及振型分析

孫 艷，李俊杰

（武漢科技大學，武漢 430065）

隨著我國城市化建設步伐的加快，交通擁堵、環境污染、人口密集、土地資源匱乏等諸多城市問題日益明顯，而城市交通問題是較為突出的一個，所以近年來我國城市軌道交通建設速度加快，各大城市也都提出了符合自身實際的城市軌道交通線網規劃和近期建設規劃［1］，各類新型的高架車站也應運而生。高架車站顧名思義就是列車行駛在地面以上的高架結構上，常見的高架車站類型主要有三種：橋梁結構式車站、空間框架式車站、橋建分離式車站。

橋梁結構式車站作為“建橋合一”結構中的一種新型車站，已逐步成為當今城市軌道交通高架車站的主流車站形式，盡管它實質上仍然是橋梁結構，但它兼具了建筑與橋梁的功能，是由一般橋梁結構延伸和拓展而來。大多數的高架橋穿梭于鬧市區和居民區，振動的產生都會對周邊的環境帶來不利的影響，例如：人處于振動環境中，將會引起人體生理和心理的效應，例如感到不舒服、麻感、頭暈、困倦，嚴重時出現出汗、頭痛、心慌甚至損害到人體心臟。當振動頻率為5Hz時，振動加速度達到0.1g時人就感到不舒服，達到0.4g時人就覺得不可忍受了［2］。因此，如何減小結構系統的振動影響具有十分重要的現實意義。

1 工程背景

以重慶軌道交通2號線某輕軌高架車站為背景，車站具有往返雙向車道，采用“T”型獨柱橋墩，站臺、軌道箱型梁、盆式橡膠支座等依次直接支撐在T型橋墩蓋梁上。車站全長63m，寬為18m，機車軌道位于車站中間，站臺分布于橋梁兩側，縱向設置一條伸縮縫；橋墩采用C40混凝土，間距10m，厚度3m，高度10m，所研究分析的車站范圍內共設有7個橋墩；站臺采用C30混凝土，高度1.5m，寬度5.1m，站臺板厚200mm，雙側布置；軌道梁采用連續鋼筋混凝土箱型梁，混凝土材料等級C40，截面形式為單箱單室，梁高2.53m，頂板寬度即為車站寬度，底板寬為7.8m；鋼軌采用60kg/m的重型鋼軌，截面面積77.45cm2，截面慣性矩Iz＝3 217cm4、Iy＝524cm4；道床采用浮置板式軌道結構（兩側和底部均設有橡膠支座），底部設中心水溝，浮置板承軌槽內側預埋PVC泄水管，鋼軌內置，兩側和底部的橡膠墊可以在橫向與縱向提供足夠的彈性，可以達到較好的減振效果。

2 模型的簡化

高架車站模型從上到下依次由站臺、鋼軌、連接鋼軌與軌下墊板的扣件、軌下墊板、浮置板式道床、橡膠墊、軌道梁、盆式橡膠支座、橋墩等幾部分組成，若要對各部分構件詳細準確地建立單元、定義單元參數及類型，將會十分復雜，難以實現，因而需要對整個結構分析模型進行一定程度的簡化與假設。建筑物的振動首先是由機車輪壓作用在鋼軌上，再由鋼軌通過扣件、軌下墊板傳到浮置板式道床，繼而傳到建筑結構上的。因此首先把鋼軌當作振源，將扣件、軌下墊板、浮置板式道床作為一個整體來考慮，在建模過程中用六面體方塊來模擬這個整體，按照0.65m的固定間距沿著車站縱向方向平行布置在橋面路基上，并采用彈簧連接的方式把鋼軌和橋梁結構連接起來；箱型梁與橋墩之間的盆式橡膠支座同樣采用彈簧連接的方式，更能接近實際情況，可以很好地體現出盆式橡膠支座在實際工程中的良好減振效果；將不考慮橋墩基礎的影響，獨柱橋墩與地面采用固結的連接方式。

3 有限單元模型及網格劃分

以大型有限元軟件ANSYS14.0為分析平臺，建立研究分析模型，采用軟件提供的PCG Lanczos法對所建模型進行模態分析。

3.1 模態分析原理

結構模態是結構振動的一種表征特性，分析結構的振動參數，如固有頻率及振型，以用于控制外加動荷載頻率或改變結構固有頻率，以避免共振現象的出現。它也是模態疊加分析方法的基礎［3］。

3.2 結構模型中所選用的單元類型

鋼軌采用三維梁單元BEAM188進行模擬，能夠很好的反映鋼軌在實際使用過程中的各種變形；箱型梁、獨柱橋墩以SOLID187單元來模擬，可以準確地反映箱梁整體性能好、結構變形小的特點；車站上部兩側的站臺結構采用SHELL181單元來模擬，它不僅有較好的彎曲能力，同時還具有良好的膜力；箱型梁與橋墩之間的盆式橡膠支座以及浮置板式道床中鋼筋混凝土支承塊下的大橡膠墊板采用彈簧單元COMBIN14來模擬。由于自振頻率ωd與阻尼比ξ存在關系式，而實際上ξ都很小，一般為0.01～0.1，則，所以結構可按無阻尼系統進行模態分析［4］。

3.3 結構模型的計算參數

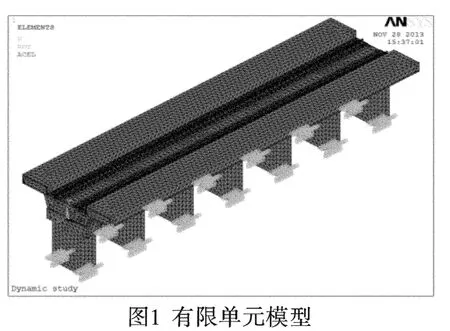
鋼軌的彈性模量為2.1×1011N/m2，泊松比0.3，密度7 850kg/m3；站臺板厚200mm，彈性模量取3.2×1010N/m2，泊松比0.2，設計密度2 500kg/m3；橋體箱型梁彈性模量為3.4×1010N/m2，泊松比0.2，設計密度2 500kg/m3，頂板寬度18m，底板寬度7.8m，梁高2.53m；橋墩彈性模量取3.4×1010N/m2，泊松比0.2，設計密度2 500kg/m3，高度10m；橋墩與箱梁連接處的盆式橡膠支座垂直剛度（彈簧系數）為1.0×1010N/m；鋼軌與橋面路基之間的整體軌道系統垂直剛度為8.0×108N/m；雙向往返車道的軌道間距為5m，扣件間距取0.65m。執行網格劃分后且模態分析前的有限單元模型如圖1所示。

4 結構的固有頻率及振型

由于結構的前幾階固有頻率對結構的振動影響最大，且發生的可能性更高。因此，提取前十階固有頻率及其對應的振型。

4.1 固有頻率

固有頻率是結構的固有屬性，見表1。

表1 固有頻率表

4.2 振型位移圖

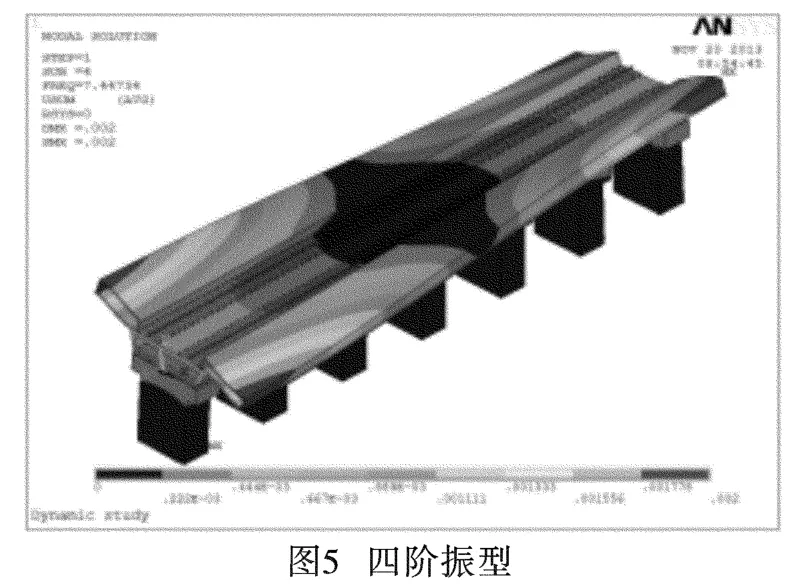
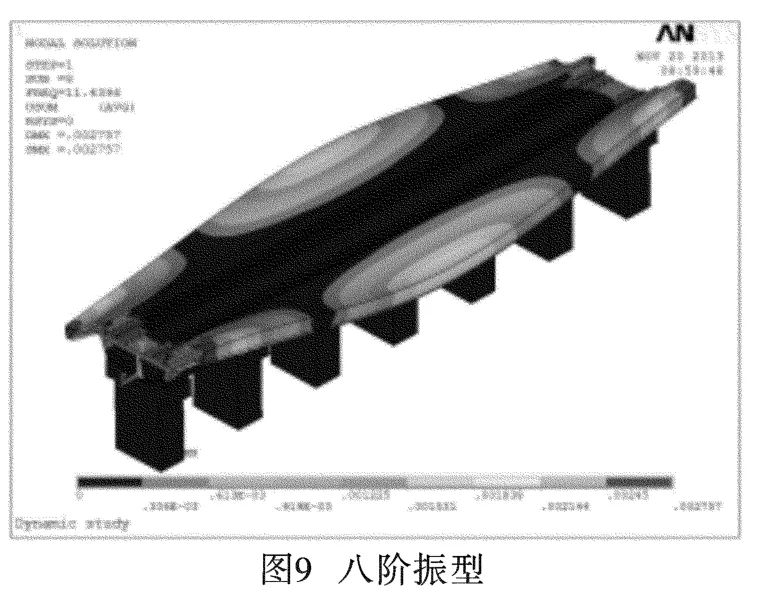
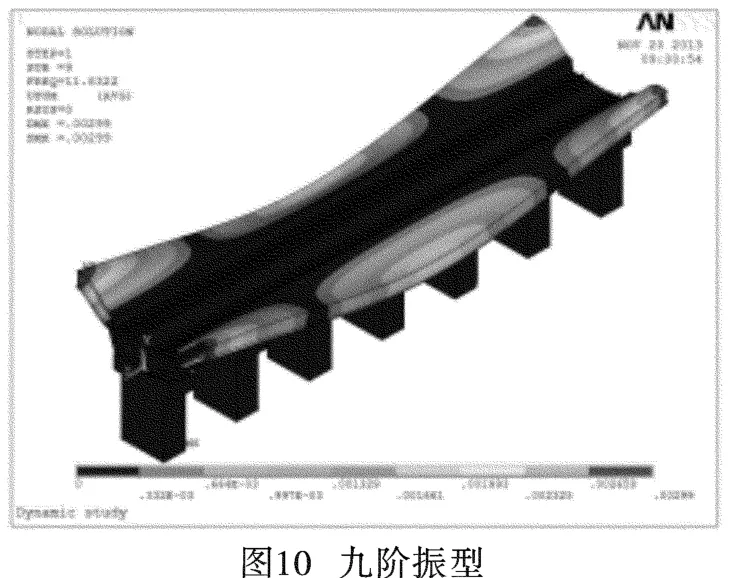
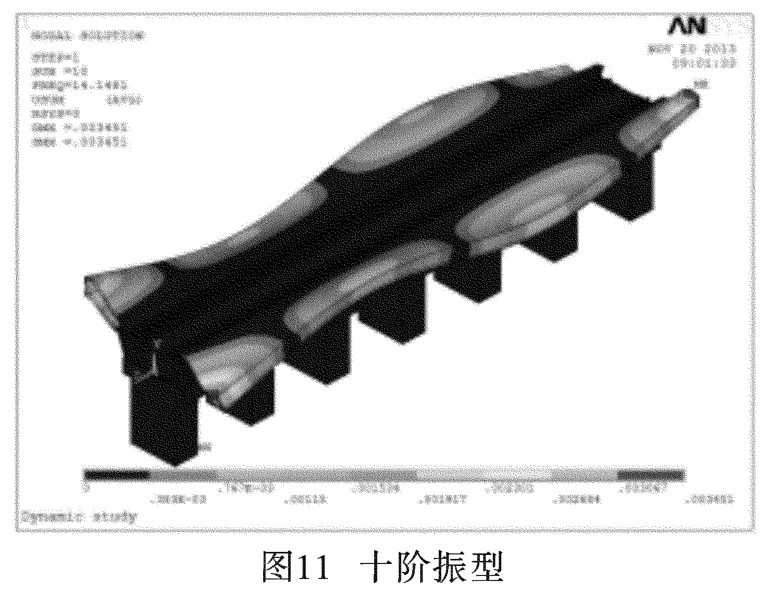
圖2～圖11分別為前十階振型位移圖。

從結構的振動位移圖可以看到，隨著產生位移的能量越來越大，整個結構系統由簡單的整體側移、平移逐漸演變成橋體上部結構的明顯波動變形：一階振型圖表現為結構整體向Z軸正方向（水平方向）側移；第二、三、六階的振型圖主要表現為結構上部兩側的站臺在豎直方向上的上下擺動；第四、五、七、八、九、十階的振型位移圖則主要表現為上部兩側站臺連續板沿著水平方向上的連續波動。結構單元節點的位移及撓曲度隨著階數的遞增而逐漸增大，結構的最大位移發生在站臺外側邊角部。

4.3 鋼軌扣件間距對固有頻率的影響

根據高速鐵路設計規范的建議，分別選取了扣件間距為0.55m、0.6m、0.65m、0.7m［5］、0.725m［6］這5種工況進行比較，分析結果表明，當扣件間距為0.60～0.65m時，結構有更多的低階固有頻率值接近于5Hz，更能滿足乘客的舒適性要求；當扣件間距為0.65m時，節點的最大振動位移值是最小的。因此，根據以上結論并結合鋼軌安全性和工程成本的經濟性，選定0.65m為最佳扣件節點間距。

5 結 語

模態分析作為一種用來確定結構振動特性的技術，通過它可以得到固有頻率、振型和振型參與系數，其中固有頻率和振型是承受動態載荷結構設計中的重要參數，也是動力學分析的出發點。

通過有限元軟件ANSYS對橋梁結構式車站的固有頻率及振型進行了研究分析，探討出不同扣件間距對結構固有頻率及振型的影響，找出最佳間距值，在一定程度上起到了有效的減振作用，更能滿足乘客的舒適性和結構的安全穩定性要求。通過此類高架車站的成功建設與運營經驗，并結合建模過程中的各項計算參數，可以通過選擇合適的鋼軌彈性模量、軌下墊層剛度與阻尼、支承塊質量、橋墩盆式橡膠支座剛度等構件來達到良好的減振效果。

［1］ 張慶賀，朱合華，莊榮.地鐵與輕軌［M］.北京：人民交通出版社，2002.

［2］ 練松良，王午生.軌道工程［M］.上海：同濟大學出版社，2006.

［3］ 彭細榮，楊慶生，孫卓.有限單元法及其應用［M］.北京：清華大學出版社，2012.

［4］ 耿傳智，田苗盛，董國憲.浮置板軌道結構的振動頻率分析［J］.城市軌道交通研究，2007（1）：23.

［5］ 邱金帥，蔡小培，安彥坤.扣件間距對無砟軌道動態軌距的影響［J］.鐵道建筑，2011（8）：106－108.

［6］ 李志紅.城際軌道交通橋梁梁端扣件節點間距研究［J］.鐵道工程學報，2009（8）：64－67.