基于BP神經網絡優化的灰色線性回歸組合模型應用分析

楊世安，周世健，饒國華

(1.東華理工大學測繪工程學院，江西 南昌330013;2.江西省科學院，江西 南昌330096)

0 引言

灰色組合模型是將灰色系統模型(主要是GM(1，1))或灰信息處理技術融入傳統模型后得到的有機組合體。GM模型具有弱化序列隨機性，挖掘系統演化規律的獨特功效，它對一般模型具有較強的融合力和滲透力。將GM模型融入一般模型建模的全過程，實現功能互補，能夠使預測精度大大提高。然灰色線性回歸組合模型可改善原線性回歸模型中沒有指數增長趨勢和GM模型中沒有線性因數的不足，故該組合模型更適用于既有線性趨勢又有指數增長趨勢的序列。

雖然灰色線性回歸組合模型能較好的模擬觀測序列，但為了使模擬更加精確，以進一步提高預測的精度。構建實測值與模擬值之間的比值序列G。目前，人工神經網絡以強大的學習能力和高擬合精度廣泛應用于各大領域，而絕大部分的神經網絡模型是采用BP網絡和它的變化形式，它是前向網絡的核心部分，并體現了人工神經網絡最精華的部分。故本文利用BP神經網絡來優化組合模型預測精度。

1 灰色線性回歸組合原理

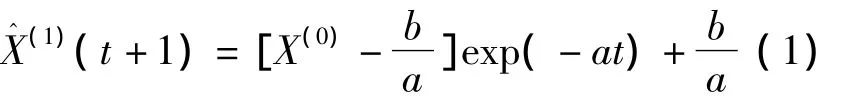
其形式可記為

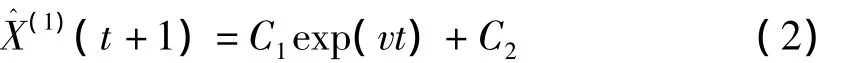
用線性回歸方程與指數方程之和擬合累加生成序列，即

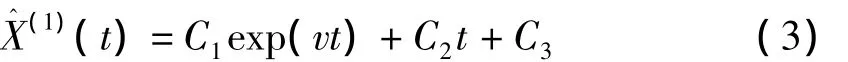
其中參數v及C1，C2，C3待定。

為求以上參數，設參數序列

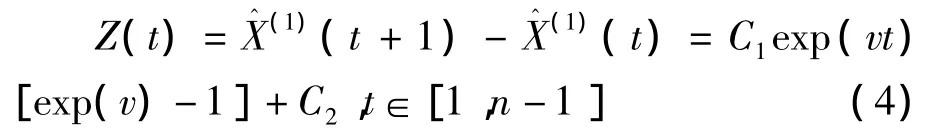
令Ym=Z(t+m)－Z(t)，則可得

由經典GM(1，1)模型［1］的原理可知

將式(4)中的X^(1)換成X(1)，由式(5)可得v的近似解，取不同的m可得不同的，以它們的平均值作為v的估值。經分析m=1，2，…，n－3，計算的的個數為(n－2)(n－3)/2，故得

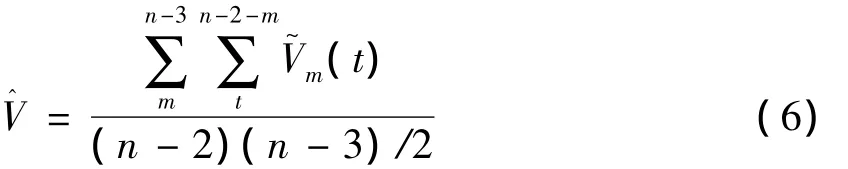
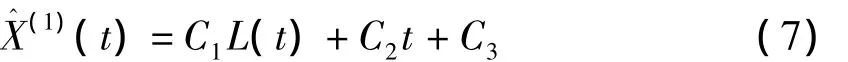
利用最小二乘法求得C1，C2，C3的估值，令

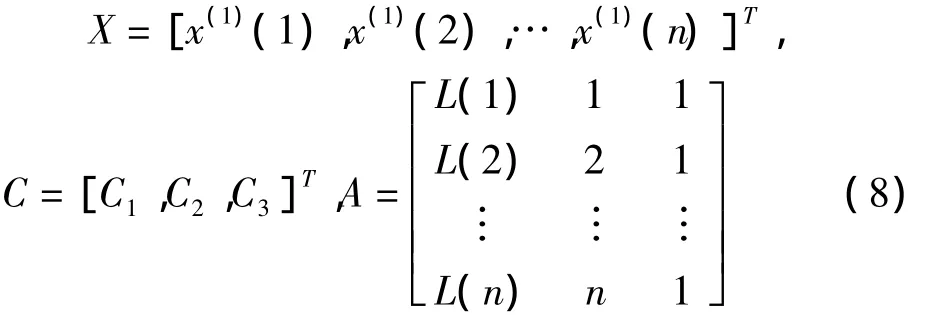
則有Y=AC，從而得

可得到生成序列的預測值為

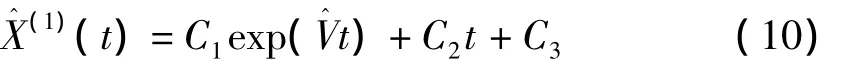
則原始序列的預測值為

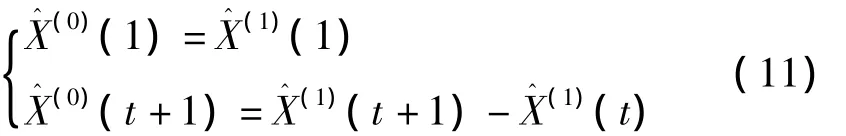
2 BP神經網絡及優化過程

BP算法的基本思想［2，3］是，學習過程有信號的正向傳播與誤差的反向傳播2個過程組成。正向傳播是，輸入樣本從輸入層傳入，經各隱層逐層處理后，傳向輸出層。若輸出層的實際輸出與期望輸出不符，則轉入誤差的反向傳播階段。誤差反向是將輸出誤差以某種形式通過隱層向輸入層逐層反傳，并將誤差分攤給各層的所有單元，從而獲得各層單元的誤差信號，此誤差信號即作為修正各單元權值的依據。這種信號正向傳播與誤差反向傳播的各層權值調整過程，是周而復始地進行的。權值不斷調整的過程，也就是網絡的學習訓練過程。此過程一直進行到網絡輸出的誤差減少到可接受的程度，或進行到預先設定的學習次數為止。

優化思想:對于初始序列X(0)，進行灰色線性回歸組合建模預測得到模擬值與預測值，針對不同的t時刻下的初始值與對應的模值有個比值關系G(t)，暫稱之為吉比率即:

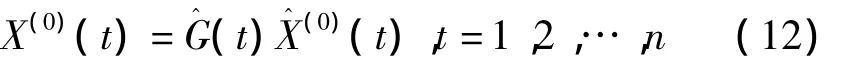
G(t)是一個新的時間序列，由于灰色線性回歸組合模型的特性，該序列表現出值大多在1附近波形震蕩變化。嘗試利用MATALB中的人工神經網絡工具箱對吉比率序列G(k)進行BP神經網絡建模，得到新的吉比率G^，在設計BP網絡時，使用5個隱含神經元，一個輸出神經元，以前兩期預測后一期做訓練。則優化后的新預測值為

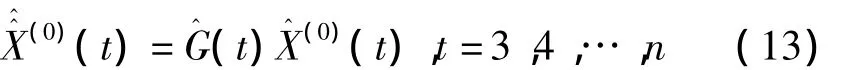
3 MATLAB實現步驟

經過以上論述，概括基于BP神經網絡優化的灰色線性回歸組合模型的MATLAB［4，5］實現的建模流程如下:

(1)1-AGO處理，將原始數據序列X0進行1次累加得X1;

(2)求解Z，由式(4)可得Z;

(5)構造X、A和C;

(6)依據最小二乘求解系數C1，C2，C3的估計值，參考式(9);

(7)由式(10)計算時間響應序列X2，將其緊鄰差分可得X0的模擬值X3，其中，X3(1)=X1(1)參考式(11);

(8)由式(12)計算吉比率G序列;

(9)由BP神經網絡對G序列進行訓練和預測;

(10)由式(13)還原出X0的新模值X4;

(11)檢驗誤差，計算殘差，方差、相對誤差和平均相對誤差。

4 數學實例分析

選取的實驗數據是，南昌市某段公路邊坡的某測樁從2012年9月至2012年1月觀測的10期沉降累計量，利用前8期建立灰色線性回歸組合模型，預測后兩期，并進行精度評定，時間相應序列為

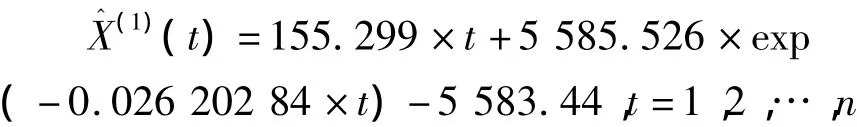
計算G(t)后，利用BP神經網絡建模，并還原出新的預測值。將優化前后的模值列于表1中，并繪制數據對比線化圖，如圖1所示。

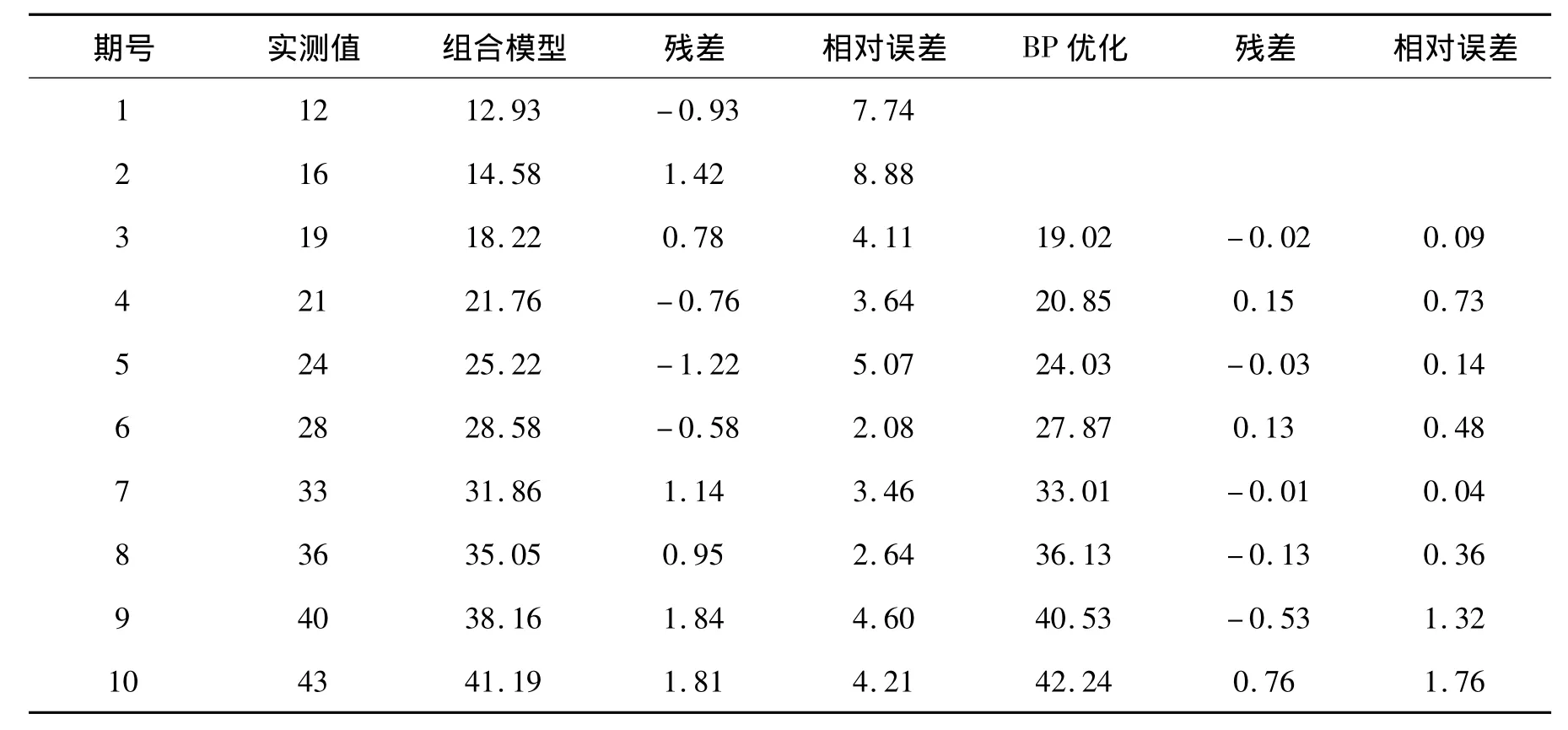
表1 灰色線性回歸組合模型預測和基于BP神經網絡優化后的數據/mm

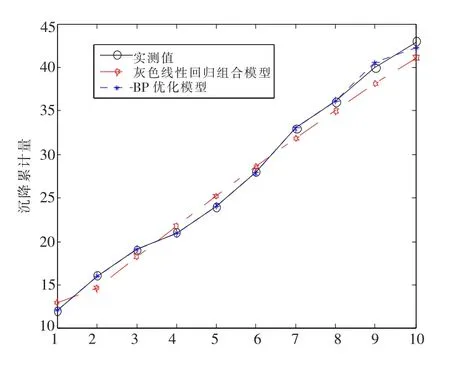
圖1 灰色線性回歸組合模型優化前后數據對比線化圖

利用灰色線性回歸組合模型建模的擬合平均相對誤差為4.69%，預測的第9、10期相對誤差為4.6%、4.21%，而使用BP神經網絡優化的擬合平均相對誤差為0.31%，預測的第9、10期的相對誤差為1.32%、1.76%。圖1同樣顯出BP優化后的數據曲線更加吻合原數據曲線。

5 結束語

用MATLAB實現灰色線性回歸組合模型算法，程序簡潔、算法清楚。并利用其自帶的神經網絡工具箱進行BP神經網絡優化，方便快捷。通過本文的數學實例證明:當實測值與預測值之間出現波動擬合時，它們的比值序列也同樣具有波動性，此時采用BP神經網絡對比值序列進行非線性擬合，具有非常高的預測精度;最后優化后的組合模型無論是擬合精度還是預測精度均比優化前的高出很多。這說明本文的優化模型用于改進灰色線性回歸組合模型是可行有效的，同樣也對變形監測數據的分析和預測具有參考價值。

［1］ 劉思峰，謝乃明.灰色系統理論及其應用［M］.北京:科學出版社，2008.

［2］ 田雨波.混合神經網絡技術［M］.北京:科學出版社，2009.

［3］ 朱 凱，王正林.精通MATLAB神經網絡［M］.北京:電子工業出版社，2010.

［4］ 唐麗芳，賈冬青，孟慶鵬.用MATLAB實現灰色預測GM(1，1)模型［J］.滄州師范專科學校學報，2008，24(2):35－37.

［5］ 胡曉東，董辰輝.MATLAB從入門到精通［M］.北京:人民郵電出版社，2010.