關于復正規矩陣的2個不等式

沈 浮，夏必臘，周堂春

(解放軍陸軍軍官學院數學教研室，安徽 合肥230031)

0 引言

矩陣不等式是矩陣理論中的一個很重要內容。隨著矩陣理論的迅速發展及其在自然科學、工程技術和社會經濟等領域的廣泛運用，關于矩陣不等式的新結果層出不窮。文獻［1］中的定理3.9指出:當A是Hermite矩陣時，則有λmin(A)E≤A≤λmax(A)E。文獻［2］中定理6.2.2又指出:當A和B為2個非負定的Hermite矩陣時，則有0≤trAB≤λmax(A)trB≤rtA·trB。這2個結果都是針對Hermite矩陣的，本文對復正規矩陣進行了研究，得出了更進一步的結論。

本文中，用Re(z)表示復數z的實部，用λmin(A)和λmax(A)分別表示Hermite矩陣A的最小特征值和最大特征值，用λRmin(A)和λRmax(A)分別表示復矩陣A實部最小的特征值和實部最大的特征值，用tr(A)記矩陣A的跡，向量x的共軛轉置用xH，E表示n階單位矩陣。

1 基本概念及相關引理

定義1:設A∈Cn×n，若對任意非零列向量x∈Cn×1，都有

則稱A為復正定矩陣(或復非負定矩陣)，記作A＞0(或A≥0)。

顯然，當A為Hermite正定(非負定)矩陣時，它也是復正定(非負定)矩陣。

定義2:設A、B∈Cn×n，如果A－B是復正定矩陣(或復非負定矩陣)，則稱復矩陣A大于復矩陣B(或稱復矩陣A大于或等于復矩陣B)，記作A＞B(或A≥B)。

本文要用到復正定(非負定)矩陣以下幾個重要結果，把它們作為引理1。

引理1［1］:(1)設A=(aij)n×n∈Cn×n，且A是復正定矩陣(或復非負定矩陣)，則Re(aii)＞0 (或Re(aii)≥0)(i=1，2，…，n)。

(2)A是復正定(非負定)矩陣的充要條件是:A+AH為Hermite正定(非負定)矩陣。

(3)復對角矩陣A=diag(λ1，λ2，…，λn)是復正定(非負定)矩陣的充要條件是:Re(λi)＞0 (Re(λi)≥0)，i=1，2，…，n。

(4)設A、B∈Cn×n，若A＞B，P為n×m的列滿秩矩陣，則PHAP＞PHBP;當P不是列滿秩時，由A≥B只能推出PHAP≥PHBP。

定義3:如果方陣A∈Cn×n滿足AAH=AHA，則稱A為正規矩陣。

引理2［3］:A∈Cn×n，則A酉相似于對角矩陣的充分必要條件是:A為正規矩陣。

引理3［4］:設A∈Cn×n是正規矩陣，則A為復正定(非負定)當且僅當A的特征值實部皆為正(非負)。

引理4［5］:設A、B∈Cn×n都是正規矩陣，則A、B可同時酉對角化的充要條件是AB=BA。

2 主要結果

下面的定理1、定理2及其推論就是本文的主要結果。

定理1:設A∈Cn×n是正規矩陣，則λRmin(A) E≤A≤λRmax(A)E。

證明:A是正規矩陣，由引理2知，存在酉矩陣U，使A=Udiag(λ1，λ2，…，λn)UH，這里λ1，λ2，…，λn必是A的n個特征值。于是由引理1的(3)、(4)知

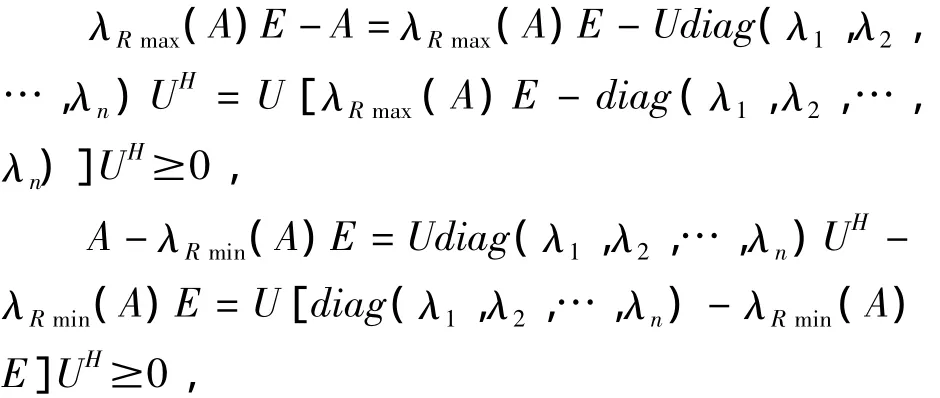
即λRmin(A)E≤A≤λRmax(A)E。

由于復正定(非負定)的正規矩陣特征值實部全為正(非負)，所以由定理1便得如下推論。

推論:設A∈Cn×n是復正定(非負定)的正規矩陣，則

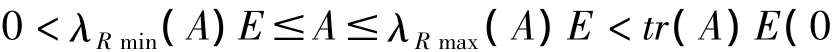
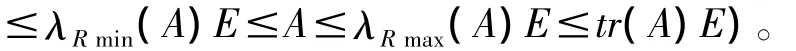
定理2:設A、B∈Cn×n是復正規矩陣，AB= BA，A、B的特征值分別為λ1，λ2，…，λn和μ1，μ2，…，μn，則當Re(λRmin(A)μj)≤Re(λjμj)≤Re (λRmax(A)μj)(j=1，2，…，n)時，Re(λRmin(A) trB)≤Re(trAB)≤Re(λRmax(A)trB)。

證明:因A、B可交換的正規矩陣，由引理4知:A、B可以同時酉對角化，即存在酉矩陣U，使得A=Udiag(λ1，λ2，…，λn)UH，B=Udiag(μ1，μ2，…，μn)UH。于是有

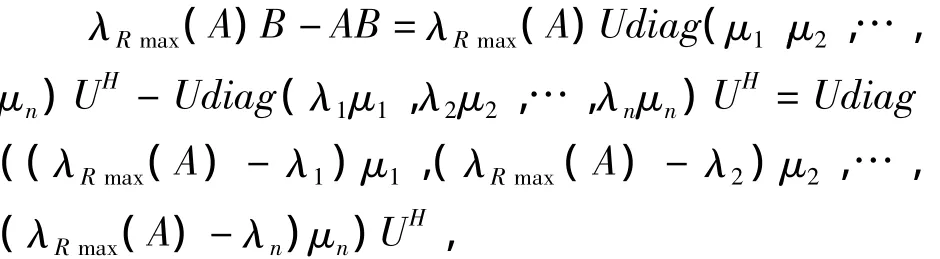
即λRmax(A)B－AB酉相似于對角矩陣。由于Re (λjμj)≤Re(λRmax(A)μj)(j=1，2，…，n)，故對角矩陣的對角元的實部全非負，從而λRmax(A)B≥AB。類似可證:當Re(λRmin(A)μj)≤Re(λjμj)(j =1，2，…，n)時，λRmin(A)B≤AB。于是得

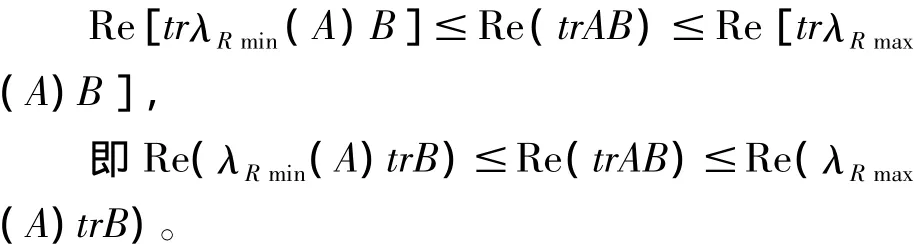
推論1:當A∈Cn×n是復正規矩陣，B∈Cn×n為非負定的Hermite矩陣時，AB=BA，Re(λRmin(A)) ·trB≤Re(trAB)≤Re(λRmax(A))·trB。

證明:設A、B的特征值分別為λ1，λ2，…，λn和μ1，μ2，…，μn，因B是非負定的Hermite矩陣，所以其特征值μi(i=1，2，…，n)非負，于是在定理2證明中出現的(λRmax(A)－λi)μi(i=1，2，…，n)實部全非負，從而λRmax(A)B≥AB，類似地可以證明:λRmin(A)B≤AB。故

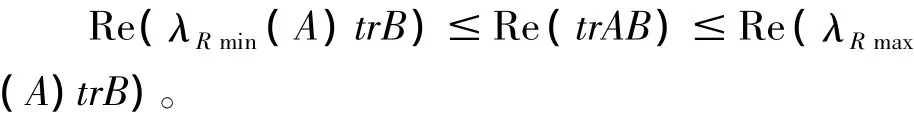
注意到trB≥0，便得Re(λRmin(A))·trB≤Re(λRmax(A))·trB。

推論2:設A∈Cn×n是非負定的正規矩陣，B∈Cn×n為非負定的Hermite矩陣，AB=BA，則0≤Re (λRmin(A))·trB≤Re(trAB)≤Re(λRmax(A))· trB。

證明:由推論1知，Re(λRmin(A))·trB≤Re (trAB)≤Re(λRmax(A))·trB顯然成立。再由trB≥0及Re(λRmin(A))≥0，便可得出推論2。

推論3:設A∈Cn×n是非負定的Hermite矩陣，B∈Cn×n為非負定的正規矩陣，AB=BA，則 λmin(A)·Re(trB)≤Re(trAB)≤λmax(A)·Re(trB)。

證明:在定理2中，如果設

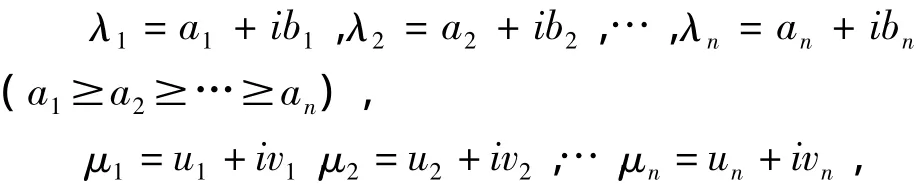
則定理2的條件Re(λRmin(A)μj)≤Re(λjμj)≤Re(λRmax(A)μj)(j=1，2，…，n)就變成

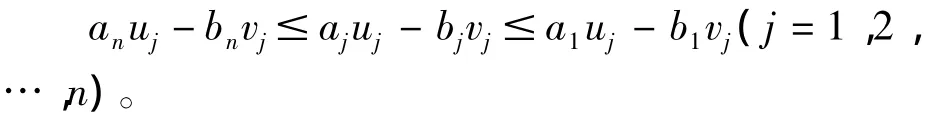
在本推論中，依條件及引理3知:所有的aj≥0，bj=0，uj≥0，(j=1，2，…，n)，所以條件

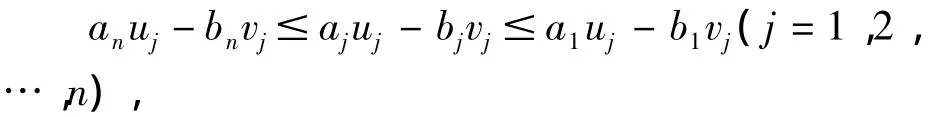
相當于

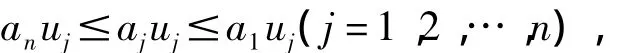
此不等式顯然成立。于是由定理2得:

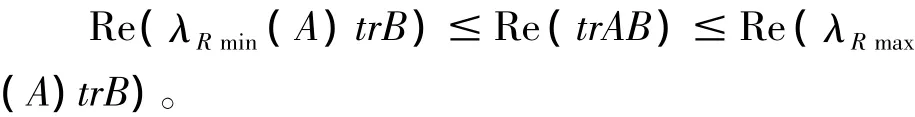
注意到A是非負定的Hermite矩陣，即λRmin(A)=λmin(A)，λRmax(A)=λmax(A)，便得

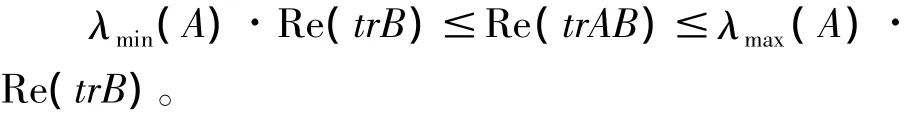
［1］ 方寶镕，周繼東，李醫民.矩陣論［M］.北京:清華大學出版社，2004:110－116.

［2］ 王松桂，吳密霞，賈忠貞.矩陣論不等式(第二版)［M］.北京:科學出版社，2006:129－131.

［3］ 程云鵬，張凱院，徐 仲.矩陣論(第3版)［M］.西安:西北工業大學出版社，2006:100－106.

［4］ 袁暉坪.關于復矩陣乘積的正定性［J］.數學的實踐與認識，2006，36(11):202－206.

［5］ 史榮昌，魏 豐.矩陣分析(第3版)［M］.北京:北京理工大學出版社，2010:115－125.

［6］ 詹興致.矩陣論［M］.北京:高等教育出版社，2008: 39－45.

［7］ 金 能.關于復正定矩陣乘積跡的估計［J］.工科數學，2002，18(4):106－108.