基于積分的數值微分算法

徐會林，郜星軍

(河南理工大學數學與信息科學學院，河南 焦作454000)

0 前言

數值微分，即由給定函數的測量數據近似求其導數，這類問題在科學研究及工程實踐中有廣泛的應用價值。如在磁共振電阻抗成像技術(MREIT)中，介質的導電率是利用生物組織內部電流產生的磁場信息重建的。基于主磁場方向磁感應強度的調和Bz算法是當前主流的導電率重建算法，而如何由磁感應強度的測量數據計算其二階導數是關鍵步驟［1］，數值微分的具體應用還體現在數字圖像特征檢測問題［2］、期權定價問題［3］、放射性廢棄物的存儲問題［4］等方面。

數值微分問題的求解，除標準的正則化方法外［5～8］，還有一些其特有的方法，如有限差分法［9］、平滑化方法［10］等。眾所周知，微分和積分是互逆的2種基本運算。積分的計算通常要借助微分實現，反過來，也可利用積分求微分，其實質是將微分運算等價轉化為第一類積分方程的求解問題［11，12］。

本文將基于微分與積分之間的互逆關系，構造數值微分的實現算法。通過把數值微分問題等價轉化為第一類積分方程的求解問題，給出了一元函數前兩階導數的近似計算方法，并通過數值算例說明了解的數值有效性。

1 一階數值微分算法

設一元函數f(x)∈C1［0，1］，u(x)為其一階導函數，即u(x)=f'(x)∈C［0，1］，則函數u和f滿足第一類的Volterra型積分方程

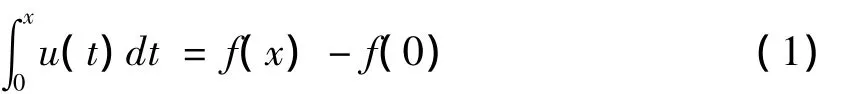
不失一般性，設f(0)=0，則有

此時，求導數u的問題就轉化為積分方程(2)的求解問題［11］。在實際問題中，函數f(x)的表達式一般是未知的，已知的只是其在某些離散點上的取值。此時，導數u或等價的積分方程(2)的求解需引入數值算法。為此，引入數值積分公式將方程(2)左端的積分項進行離散，將積分方程的求解近似為線性方程組的求解，這就是求解積分方程的數值積分法［13］。

首先將區間［0，1］進行n等分，得n+1個離散節點xi=ih，i=0，1，…，n，其中h=1/n為離散步長。為方便記號，將f(x)和u(x)在離散節點上的取值分別記為fi=f(xi)，ui=u(xi)。當x= x1時，引入梯形求積公式可得

當x=xi，2≤i≤n時，引入復化梯形求積公式可得

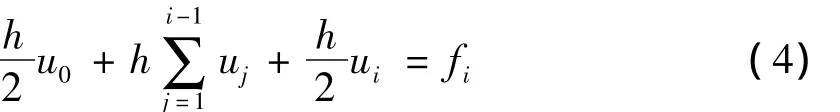
聯立式(3)、式(4)可得如下線性方程組

當u0=u(0)=f'(0)已知時，求解可得

實際計算時，u0往往是未知的，它的求解需借助其它方法，如利用向前差分格式求解可得u0= f(x1)/h。

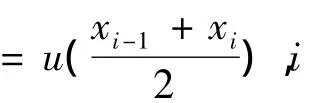
當x=xi，2≤i≤n時，引入復化中點求積公式可得

聯立式(7)、式(8)可得如下線性方程組

求解線性方程組(9)可得一階導數在中點處的近似值。

2 二階數值微分算法

設f(x)∈C2［0，1］，u(x)為其二階導數，即u (x)=f″(x)∈C［0，1］。不失一般性，總是可以假設f(0)=f(1)=0，否則f(x)－f(0)+x(f(0)－f (1))滿足該假設且與f(x)有相同的二階導數。因此有

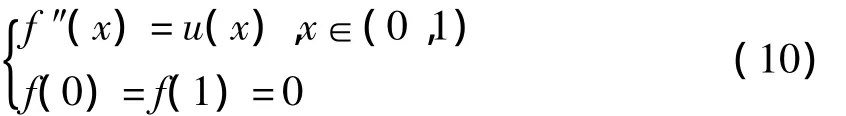
求解該常微分方程可知函數f(x)及其導數u(x)滿足如下關系［14］

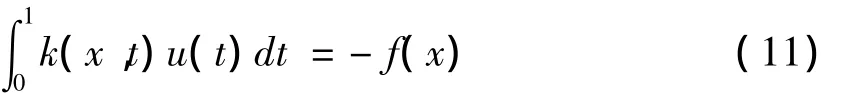
方程(11)為第一類的Fredholm型積分方程，引入復化梯形求積公式可得，當x=xi，0≤i≤n時，

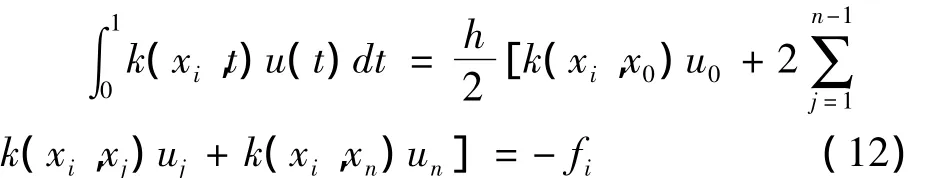
當i取0，1，…，n時，可得n+1個方程，聯立得如下線性方程組

注意到x0=0，xn=1，所以左端系數矩陣的第一行、第一列、最后一行以及最后一列的元素均為零，將方程組(13)簡化可得

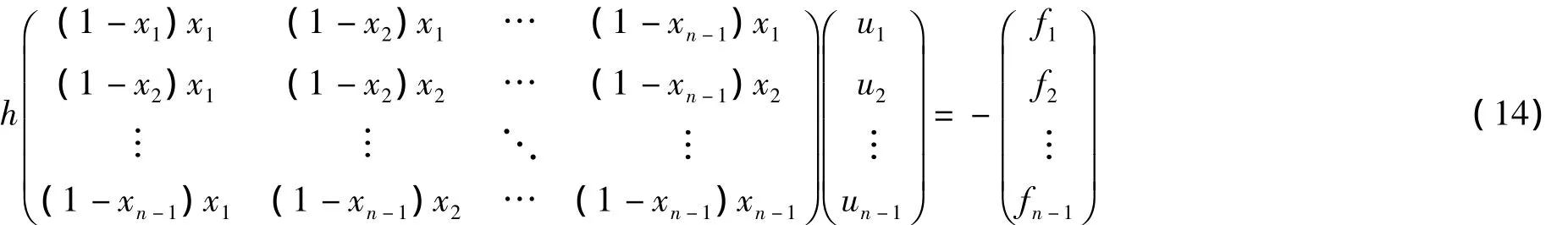
求解可得二階導數在離散節點處的近似值。

3 數值實驗

在前兩節中，分別給出了基于積分的一階及二階數值微分算法。在本節中，將通過算例說明上述算法的數值有效性。

算例1:已知函數f(x)=x4－2x2+x，x∈［0，1］，求其前兩階導數。

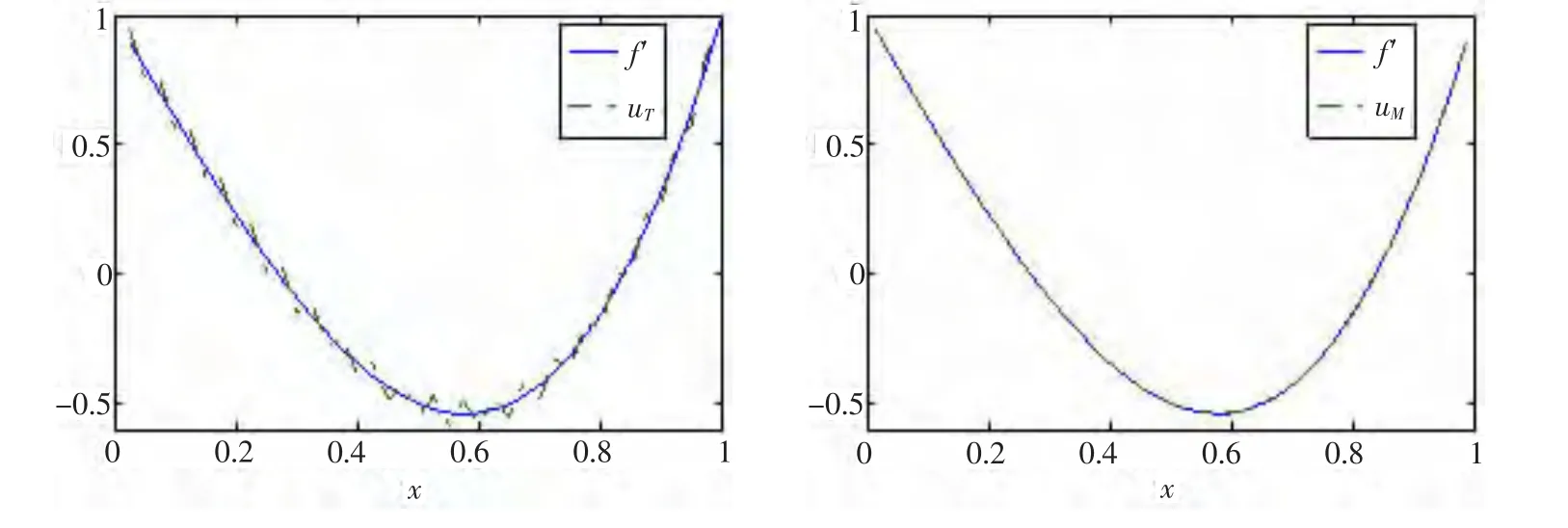
圖1 n=40時，分別利用式(5)和式(9)求得的一階導數的近似值uT，uM以及精確的一階導數f'的圖像

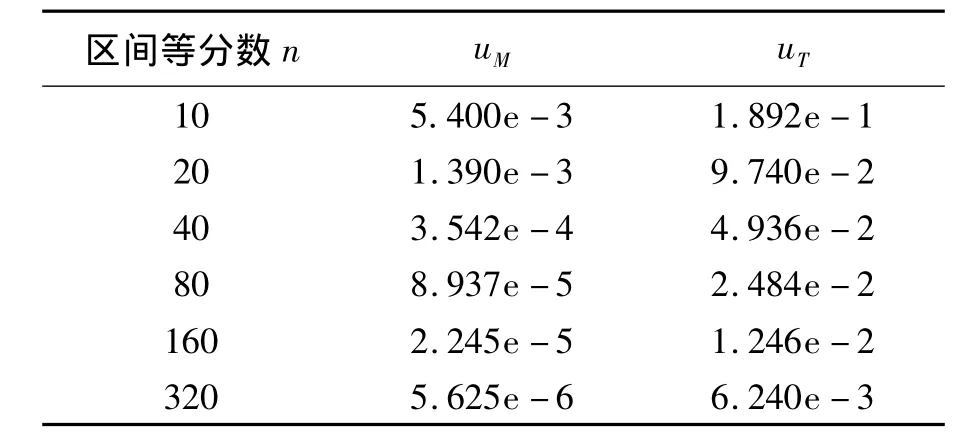
表1 算例1中等分數n取值不同時，一階導數的近似值uM和uT的誤差水平

下面，利用式(14)計算二階導數的近似值。在圖2中，給出了當n=40時，利用式(14)求得的二階導數的近似值u及精確值f″的圖像。從圖2中可以看出，二階導數的近似值與精確導數是基本吻合的。進一步，在表2中給出了二階導數的近似值的誤差水平，從中可以看出近似解的計算是二階收斂的。

算例2:已知函數f(x)=sin(5πx)，x∈［0，1］求其前兩階導數。

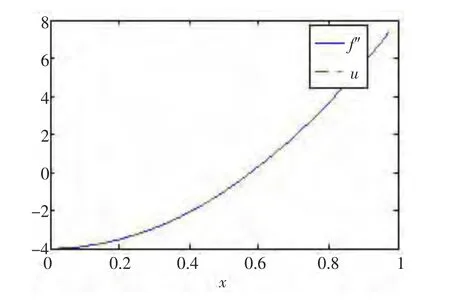
圖2 n=40時，利用式(14)求得的二階導數的近似值u及精確的二階導數f″的圖像

首先，分別利用式(5)和式(9)計算一階導數的近似值。在圖3中，給出了當n=40時，分別利用式(5)和式(9)求得的一階導數的近似值uT，uM以及精確的一階導數f'的圖像。從中可以看出，近似解uM在數值計算中的優越性。進一步，在圖4中給出了當n=40時，利用式(14)求得的二階導數的近似值u及精確的二階導數f″的圖像。從中可以看出，二階導數的近似值與精確導數是基本吻合的。近似導數的誤差分析與算例1是類似的，在此不再贅述。

表2 算例2中等分數n取值不同時，二階導數近似值u的誤差水平

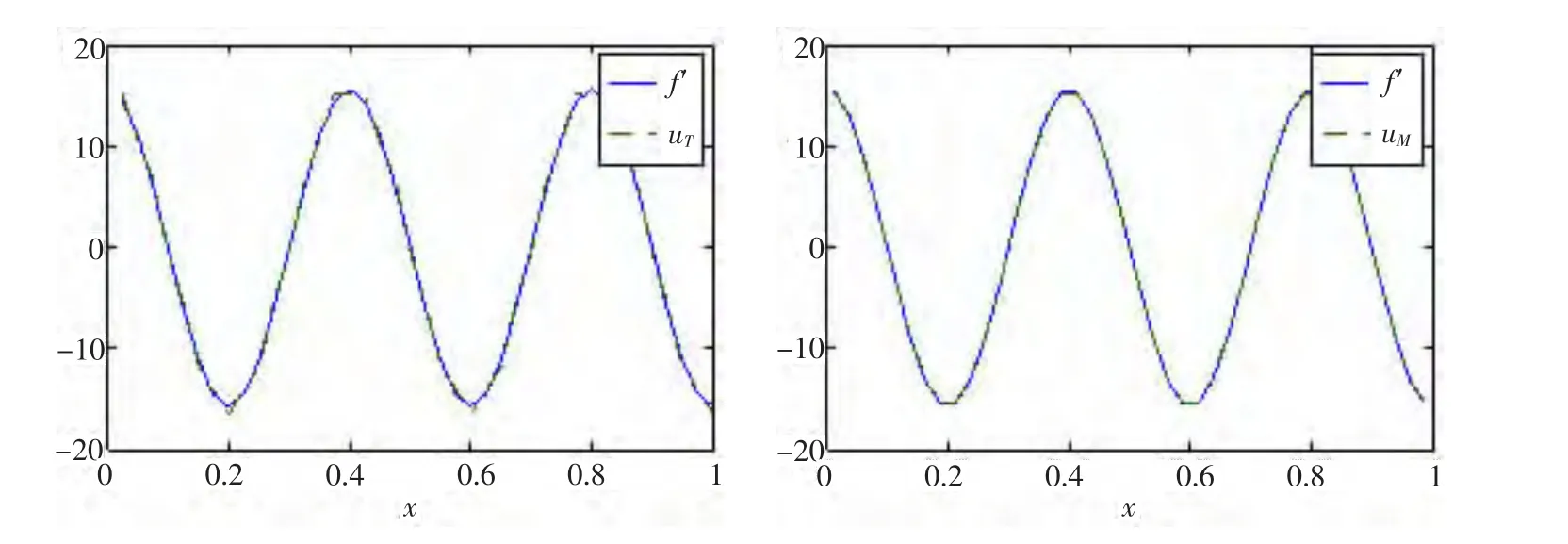
圖3 n=40時，分別利用式(5)和式(9)求得的一階導數的近似值uT，uM以及精確的一階導數f'的圖像

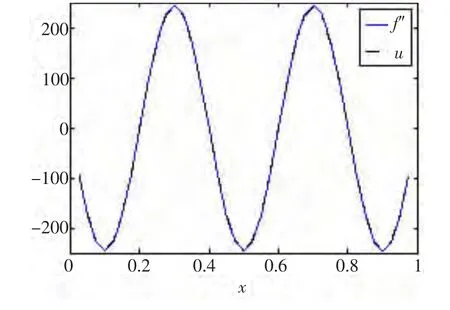
圖4 n=40時，利用式(14)求得的二階導數的近似值u及精確的二階導數f″的圖像

［1］ Seo J K，Woo E J.Magnetic resonance electrical impedance tomography(MREIT)［J］.SIAM Review，2011，53(1):40－68.

［2］ Demigny D.On optimal linear filtering for edge detection［J］.IEEE Transactions on Image Processing，2002，11(7):728－737.

［3］ Hein T，Hofmann B.On the nature of ill-posedness of an inverse problem arising in option pricing［J］.Inverse Problems，2003，19(6):1319－1338.

［4］ Mohankumar N，Auerbach S M.On the use of higherorder formula for numerical derivatives in scientific computing［J］.Communications in Computational Physics，2004，161(3):109－118.

［5］ Wang Y B，Jia X Z，Cheng J.A numerical differentiation method and its application to reconstruction of discontinuity［J］.Inverse Problems，2002，18(6):1461－1476.

［6］ Wei T，Hon Y C，Wang Y B.Reconstruction of numerical derivatives from scattered noisy data［J］.Inverse Problems，2005，21(2):657－672.

［7］ Wang Z Z，Wen R S.Numerical differentiation for high orders by an integration method［J］.Journal of Compu-tational and Applied Mathematics，2010，234(3):941－948.

［8］ 王澤文，溫榮生.一階和二階數值微分的Lanczos方法［J］.高等學校計算數學學報，2012，34(2): 160－178.

［9］ Lu S，Pereverzev S V.Numerical differentiation from a viewpoint of regularization theory［J］.Mathematics of Computation，2006，75(256):1853－1870.

［10］ Murio D A，Mejia C E，Zhan S.Discrete mollification and automatic numerical differentiation［J］.Computers and Mathematics with Applications，1998，35(5): 1－16.

［11］ Ahn S，Choi U J，Ramm A G.A scheme for stable numerical differentiation［J］.Journal of Computational and Applied Mathematics，2006，186(2):325－334.

［12］ Xu H L，Liu J J.Stable numerical differentiation for the second order derivatives［J］.Advances in Computational Mathematics，2010，33(4):431－447.

［13］ 沈以淡.積分方程(第三版)［M］.北京:清華大學出版社，2012.

［14］ 徐會林，王澤文.二階數值微分的積分方程方法［J］.江西科學，2009，27(1):108－112.

［15］ 孫志忠，袁慰平，聞震初.數值分析(第二版)［M］.南京:東南大學出版社，2002.