基于引力搜索算法的含分布式電源配電網重構

韋勝旋，劉前進，施 超，許慧銘

(華南理工大學 電力學院，廣東 廣州510640)

0 引言

配電網具有閉環設計、開環運行的特點。配電網重構是在滿足系統正常運行允許的條件下，通過控制分段開關或聯絡開關的通斷來改變饋線的拓撲結構，并保持網絡的輻射狀而沒有孤立節點，實現減少功率損耗、提高可靠性、平衡負荷等目的［1］。分布式電源(Distributed Generator，DG)接入配電網已成為研究熱點和必然趨勢，大量DG 接入改變了配電網結構，會使配電系統的網損、電壓分布、電壓穩定性、短路電流等發生變化，這種變化與DG 的安裝位置、容量直接相關。目前的DG 規劃主要在網絡拓撲結構不變的情況下選址和定容，為保證配電網時刻運行在最優狀態，應根據網絡結構的變化相應的調整可調度DG 的出力。

配電網絡重構是一個復雜的多目標非線性整數組合優化問題，國內外學者對此進行了大量研究。文獻［2］采用傳統的啟發式算法對配電網絡進行重構求解，此類算法計算速度快，但一般只能得到次優解。為了獲得最優解，文獻［3］采用自適應遺傳算法、文獻［4］提出基于節點集的蜜蜂進化型遺傳算法、文獻［5，6］分別提出基于類電磁機制和基于全有效解整數微分進化算法的配電網重構。文獻［7］考慮了不同類型DG 的影響，采用領域免疫搜索算法來尋優。文獻［8］建立了含分布式電源的基于多種負荷方式的配電網重構模型，采用了二進制粒子群算法;文獻［9］將基于多Agent 聯盟機制的相關理論引入到含DG 配電網重構研究中。上述文獻大多以降低網損為優化目標，較少涉及對系統供電可靠性的優化。在實際運行中，供電部門對供電服務越來越重視，因此在配電網重構中應該對網損及可靠性的影響。

本文提出以一種新的進化算法，引力搜索算法(Gravitational Search Algorithm，GSA)來解決含分布式電源的配電網多目標重構問題。它已被證明可以獲得比粒子群算法更好的最優解［10］。多目標優化中各目標具有不同的量綱和數量級，因此引入隸屬度對各目標進行模糊化處理，然后根據決策函數從帕累托前沿中擇取最優解。對IEEE33 節點配電網絡系統進行計算，比較分析了不同的優化方案和不同算法的運算結果，仿真結果驗證了所提出模型和求解方法的正確有效。

1 含DG 配電網重構的數學模型

1.1 目標函數

(1)系統有功損耗

式中:Ii和Ri分別是第i 條支路的電阻和流過的電流;SWi是第i 條支路聯絡開關或分段開關的狀態;Nbranch是帶開關支路數，0 和1 分別表示開關斷開和閉合;PDGi是第i 個功率可調DG 發出的有功功率;NDG為可調度DG 的個數。

(2)系統缺供電量

缺供電量是反應中低壓配電網可靠性的重要指標。設一個配電網含有n(n ＞1)個節點，0節點代表源節點。其余節點為負荷節點，有功功率為Pi，i ∈(1，2，…，n- 1)。第i 節點的ENS 可以用式(2)計算［11］:

式中:Pi是節點i 的負荷的有功功率;V∈(0，1，…，n-1)表示配電網中各節點的支路的集合;Ui，j是所有與i 節點連接支路的與故障修復時間有關的可靠性參數;U'i，j是所有與i 節點連接支路的與故障定位時間有關的可靠性參數。Ui，j和U'i，j與下列因素有關［12］:

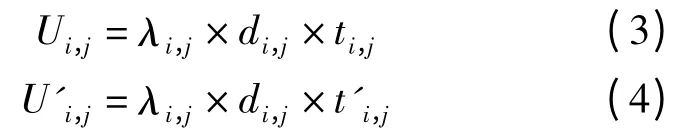
式中:λi，j和di，j分別是節點i 和節點j 之間支路的故障率和長度;ti，j和t'i，j分別是節點i 和節點j 之間支路的平均故障修復時間和平均故障定位時間。

例如，一個簡單的配電網結構如圖1 所示。對于節點3 的ENS，如果支路1 或支路2 發生故障，那么節點3 的停電時間為故障支路的修復時間;如果支路3 發生故障，那么節點3 的負荷的停電時間為故障定位和非故障線路合閘所需要的時間。因此，節點3 的ENS 為:

因此，整個系統的ENS 可以表示為:

圖1 簡單配電網單線圖

1.2 約束條件

配電網重構需滿足以下約束條件:(1)拓撲約束:重構后的配電網必須為輻射狀結構;(2)供電約束:配電網必須滿足負荷的供電，不能有孤立節點;(3)電壓幅值:各節點的電壓不能超過正常運行允許的上下界，Vmin≤Vi≤Vmax;(4)支路容量:支路傳輸的實際功率不能超過其允許容量，Imin≤Ii≤Imax。

在配電網的潮流計算中，DG 一般可以建模為PV 節點或PQ 節點。當DG 被建模為PV 節點時，它必須吸收一定的無功功率來保持電壓恒定。因此，在本文中采用DG 的PQ 模型來進行潮流計算。

2 改進引力搜索算法

簡單介紹GSA 算法的流程如下。

假設在d 維搜索空間里有N 個粒子，第i 個粒子的位置為，根據牛頓引力定律，第i 個粒子受到第j 個粒子的作用力為:

式中:t 為算法的迭代次數;Maj為第j 個粒子的主動引力質量;Mpj為第j 個粒子被動引力質量;G(t)為引力時間常數，以下列方式更新:

式中:G0為初始時刻引力常數，一般取值100;α一般取20;T 為算法最大迭代次數。

然后，計算粒子i 的適應度函數值fi(t)，將第t 次迭代時的最優適應度和最差適應度分別記為Fbest(t)和Fworst(t)，通過下式計算每個粒子的質量:

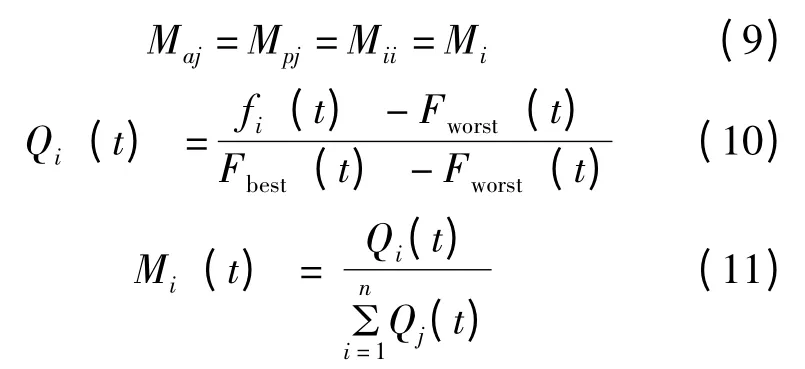
對第i 個粒子，受到來自其他粒子引力合力用引力的隨機加權和表示為:

式中:rand1是介于0 到1 之間的隨機數。

根據牛頓第二定律，粒子運動的加速度為:

那么，粒子運動速度及位置根據下式更新:

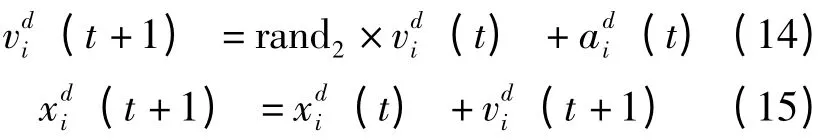
式中:rand2是介于0～1 之間的隨機數。

GSA 算法與傳統的PSO 算法相比，有以下優勢:在粒子群算法中，粒子的運動方向僅與粒子個體極值Pbest和群體極值Gbest有關，而GSA 算法中，粒子的運動與所有粒子的合引力有關，這樣可以有更高的收斂速度且不容易陷入局部最優。

3 多目標求解方法

3.1 模糊化處理多目標函數

在多目標函數的優化求解中，各子目標的相關性低甚至相互矛盾，要使多個子目標同時達到最優值比較困難。模糊集合理論以適當的隸屬度函數，建立模糊集合，可以有效地處理優化過程中的不確定現象［13-14］。

多目標中的第i 個目標Fi的隸屬度如下:

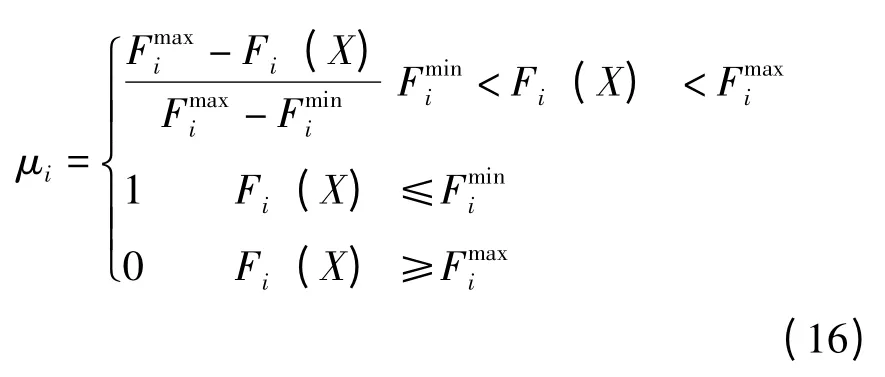
3.2 Pareto 最優解

本文運用Pareto 最優解理論來分析多目標優化的可行解之間的關系。Pareto 最優解理論是基于“支配”的概念，在多目標優化問題中，如果解X1和X2滿足以下關系時，則稱解X1支配X2。

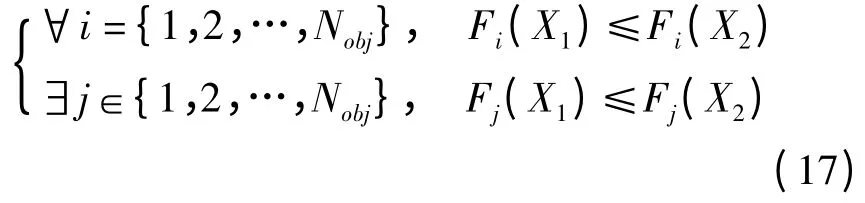
式中:Nobj是優化函數中目標的個數。

3.3 模糊決策

在最終得到的Pareto 前沿中選取最具有實際工程價值的最優解，可以采用模糊決策的方法。將每次迭代計算獲得的非支配最優解集綜合起來，通過決策函數來擇取最優解［15］。根據下式從非支配最優解集中選取最優解:

式中:Nobj是目標個數;βk是第k 個目標的權重;m 是非支配解的個數。

根據各目標的重要程度設置各目標的權重，選取具有最大隸屬度函數值的Nμ作為最優解。

整個算法流程如圖2 所示。

圖2 引力算法搜索流程圖

4 算例分析

為了檢驗本文提出方法的有效性，本文采用IEEE33 節點配電網絡系統，系統結構圖如圖3 所示。圖中，分支33～37 裝設常開聯絡開關，其余分支裝設分段開關。負荷、網絡參數以及與系統ENS 有關的可靠性參數見文獻［15］。

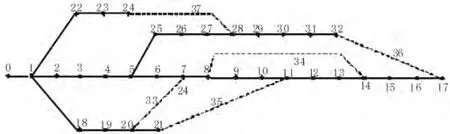
圖3 IEEE33 節點測試系統圖

通過優化計算，將以單目標和多目標的優化結果列于表1。從表1 中可知，分別以網損最小、ENS 最小以及綜合考慮兩種指標的配電網重構結果。當僅以有功網損最小為目標時，網損從201．24 kW 下降到138．04 kW，并且ENS 也明顯降低。值得注意的是:僅以ENS 最小為優化目標時，網損反而比初始網絡有所上升，并且開關操作次數為8 次。綜合考慮兩種優化目標時，算法搜索到的非劣解如圖4 所示，圖中非劣解構成了帕累托面。當兩個優化目標的權重因子β1=β2=0．5，根據式(18)擇取最優解列于表1 第3 行?？捎^察到網損和ENS 同時降低，表明優化算法取得了比較好的結果。

表1 以網損最小為目標的重構結果

圖4 非劣解空間分布

在算例原有基礎上接入4 個DG，DG 的最大輸出容量均為500 kW。其中，節點5 和節點15接入功率恒定類型DG，節點11 和節點30 接入功率可調類型DG。

接入DG 后配電網的優化重構結果如表2 所示。由表2 可知，經過配電網重構并優化可調度DG 的有功輸出，可使網損相比于重構前大幅降低，ENS 顯著下降。但是，當僅以降低網損或ENS 為優化目標時，勢必引起另一目標值的惡化。因此，應當引入帕累托前沿來為實際運行提供足夠的參考?？筛鶕繕说闹匾栽O置權重，本例中仍然設權重因子β1=β2=0．5，然后根據式(18)選取最優解列于表2 中。結果表明，網絡重構后網損和ENS 值有較大幅度降低。通過配電網重構，并優化可調度DG 的有功輸出，加入DGs的配電網達到了最優網架結構。

表2 以網損最小為目標的重構結果

為比較GSA 算法在復雜問題尋優過程的優勢，圖5 中給出了含分布式電源配電網優化重構、以網損最小為目標時，GSA 算法、PSO 算法和GA算法的收斂曲線。從圖中可知，GSA 算法在5 次迭代之后即可達到最優解，收斂速度高于其他兩種算法。

圖5 IEEE33 節點測試系統

5 結論

本文以網損和缺供電量最小為目標，以開關組合以及分布式電源注入功率為控制變量，提出一種新的算法用于含分布式電源的多目標配電網重構。根據所獲得的帕累托最優解，按目標權重因子利用模糊決策擇取最優解。通過算例表明結果滿足系統正常運行要求，并且具有較高的速度。

［1］鄧桂秀，江修波，蔡金錠．基于混沌二進制粒子群算法的配電網重構研究［J］．電力科學與工程，2013，29(9):34-37．

［2］González Alezeia，Echavarren F M，Rouco L，et al．A sensitivities computation method for reconfiguration of radial networks［J］．IEEE Trans．on Power Systems，2012，27(3):1294-1301．

［3］許奎，楊波，李錄兵，等．改進自適應遺傳算法在配電網重構中的應用［J］．電力科學與工程，2012，28(2):37-40．

［4］王超學，呂志奇，董慧，等．基于改進蜜蜂進化型遺傳算法的含分布式電源的配電網重構［J］．電力系統保護與控制，2012，40(15):52-56．

［5］李如琦，李芝榮，凌武能，等．基于類電磁機制算法的配電網重構［J］．電力系統保護與控制，2012，40(14):116-120．

［6］曹文輝，彭春華，郭劍峰，等．基于全有效解整數微分進化算法的含分布式發電配網重構［J］．電力系統保護與控制，2013，41(11):105-110．

［7］劉暢，黃民翔．含多種分布式電源的配電網重構優化研究［J］．電力系統保護與控制，2013，41(6):13-18．

［8］劉宏江，李林川，張長盛．基于多種負荷方式的含分布式電源的配電網重構［J］．電力系統保護與控制，2012，40(11):117-121．

［9］雷振，韋鋼，言大偉，等．基于多Agent 聯盟算法的含分布式電源配電網重構［J］．電力系統保護與控制，2012，40(10):95-100，105

［10］Rashedi E，Nezamabadi-pour H，Saryazdi S．GSA:a gravitational search algorithm［J］．Inf．Sci．，2009，179(13):2232-2248．

［11］Endreneyi J．Reliability modeling in electric power systems［M］．NewYork:Wiley，1978．

［12］Càrcamo-Gallardo A，García-Santander L，Pezoa J E．Greedy reconfiguration algorithms for medium-voltage distribution networks［J］．Power Delivery，IEEE Transactions on，2009，24(1):328-337．

［13］郭創新，游家訓，彭明偉，等．基于面向元件神經網絡與模糊積分融合技術的電網故障智能診斷［J］．電工技術學報，2010，25(9):183-190．

［14］洪蘆誠，石立寶，姚良忠，等．計及風電場發電功率不確定性的電力系統模糊潮流［J］．電工技術學報，2010，25(8):116-122，130．

［15］Niknam T．An efficient multi-objective HBMO algorithm for distribution feeder reconfiguration［J］．Expert Systems with Applications，2011，38(3):2878-2887．