太陽能換熱系統的機理建模及研究

曹丁元，金秀章，孫小林，謝澤坤

(華北電力大學 控制與計算機工程學院，河北 保定071003)

0 引言

近些年環境污染、資源短缺一直是人們討論的熱門話題，具有無污染、可再生、經濟、清潔等優點的太陽能成為專家學者的研究對象。西安交通大學的魏進家教授提出了復合拋物面聚光器(CPC)型太陽能光伏/光熱聯合利用(PV/T)系統［1］。采用CPC 聚光器的光電和光熱相結合的PV/T 系統，當聚光比確定后，影響系統性能的主要參數是太陽電池的工作溫度。因此，確定太陽電池的工作溫度對于系統設計具有指導意義。目前為止，國內外很多學者對CPC-PV/T 系統的性能分析進行了不少研究［2～6］，但是涉及CPC-PV/T 綜合系統中太陽電池溫度的建模報道尚少。本文將對系統中太陽電池工作溫度的機理模型建立進行討論。機理建模［7］是在充分了解了受控對象、執行機構及系統內一切元件的運動規律，將這些運動規律用數學模型表示出來的過程。機理建模一直以來廣泛應用于各個領域［8，9］，具有理論依據嚴密，在任何狀態下使用都不會引起定性錯誤的優點。

1 數學模型分析

CPC-PV/T 系統簡圖如圖1 所示，它主要由兩部分構成:太陽能光電系統以及太陽能換熱系統。太陽能光電系統是PV 電池板接收到來自聚光器的光照而產生電能的系統;太陽能換熱系統是下層流道中的流體吸收PV 電池板的廢熱，從而使電池板溫度處在最佳工作點，同時產生可利用的熱能的系統。本文主要對太陽能換熱系統的模型進行分析。

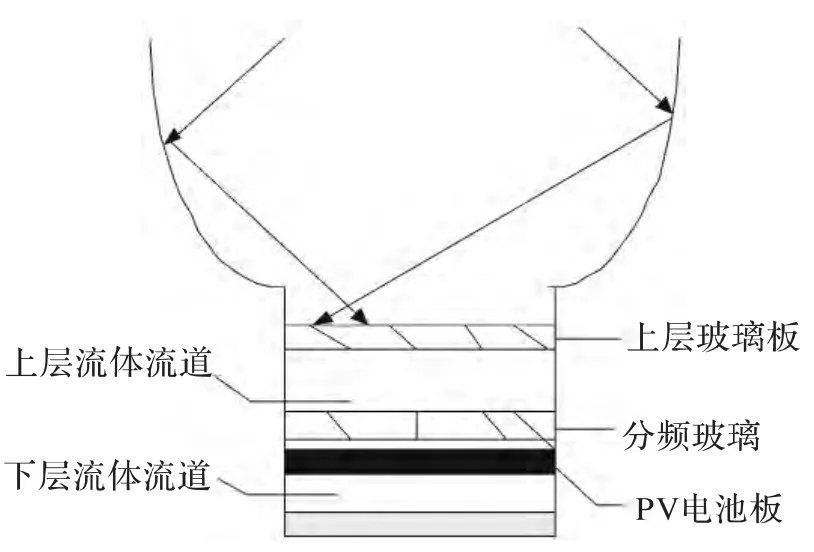
圖1 CPC-PV/T 系統簡圖

電池板的溫度主要受太陽輻射和下層流體流量的影響。太陽輻射照射到光伏電池上，會使電池板的溫度升高，從而影響到系統的光電效率。為了降低電池板的溫度，使其處在最佳的工作溫度下，本課題采用了平板PV/T 集熱器，當下層流體流過電池板，帶走電池板的廢熱，即降低了電池板的溫度，又提高了流體的溫度，實現了熱量的充分利用。

對于下層流體與電池板的熱交換部分，建模方法分為集總參數建模法［10，11］和分布參數建模法［11，12］。在流體與電池板導熱過程中，流體與電池板的狀態參數不僅是時間而且還是空間的函數，具有明顯的分布參數特點。這種分布參數的動態模型都是非線性偏微分方程組，這些偏微分方程組含有長度和時間兩個自變量。這樣一個分布參數系統的非線性模型是十分復雜的，計算也有一定難度。為了簡化問題，在建立數學模型時，將下層流道內的介質狀態參數看成是均勻一致的，并在空間位置上選定一個有代表性的點，利用這一點介質的參數作為環節的集總參數。在這種簡化假定下建立的模型就是集總參數模型。

為了便于分析，需要對換熱管道作幾個合理的簡化假設:

(1)電池板無軸向導熱;

(2)下層流道內液相介質為不可壓縮流體;

(3)忽略流體的軸向傳熱;

(4)電池板與下層流道的換熱系數為常數;

(5)同一橫截面的流體的參數相同;

(6)電池板沿下層流道長度方向的放熱量均勻。

1.1 分布參數建模

電池板與下層流道簡圖如圖2 所示，在上述簡化假設條件下，可列出距入口x 處的微分流道段dx 中在單位時間內的熱平衡方程如下:

圖2 電池板與下層流道簡圖

下層水熱平衡方程為:

式中:ρw，cw，t1分別為下層水的密度、比熱容、入口溫度;tc為電池板的溫度;Aw為流體流道換熱面積;f 為流體流道內橫截面積;h 為電池板導熱系數;L 為電池板長度;D 為下層流體的質量流量。上式整理后得

對于電池板，其能量平衡方程為:

式中:mc，cc分別為電池板的質量和比熱容。

電池板吸收的太陽輻射的熱量:

式中:ηth為光伏電池光熱轉換效率;S 為玻璃蓋板對太陽光的透射率;ηc為分頻玻璃的分頻效率;k 為聚光比;Ac為電池板的面積;G 為太陽輻射強度，可測量。

將(2)式代入上式，整理后得

電池板的溫度變化的原因可以來自于下層流道流體的流量(流體的初始溫度為恒定值)或者光照強度。在不同的擾動下，電池板溫度的動態特性是不同的。文獻［13～15］等分別針對不同的擾動因素，通過拉普拉斯(Laplace)變換，求出方程組的解析解。本文對不同擾動同時發生求出解析解。

對式(1)、(3)兩式化為增量形式，然后進行二元拉氏變換，消去中間變量Δt1(x，s)得:

對(4)式進行求解得到電池板初始溫度、流量和光照強度3 項擾動同時存在時的疊加響應為:

式中:tc0(s)為電池板初始溫度。

為了得到各個擾動對系統的獨立作用，分別令其他兩個擾動為零。對于初始溫度擾動，令D(s)=0，G(s)=0，最后得到其傳遞函數為

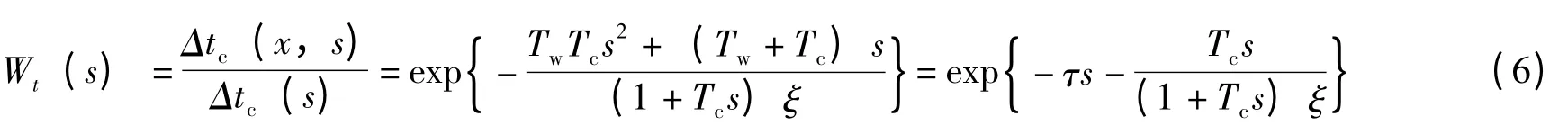
同理，可以得到太陽光照強度ΔG(s)和水工質流量ΔD(s)擾動下的傳遞函數分別為

由于式(6)～(8)均為超越型傳遞函數。計算起來很不方便，因此，采用低階逼近將它們進行簡化［2，3］。具體方法是將上述傳遞函數在s=0 附近的領域內展開為泰勒級數的形式，并與假設的傳遞函數相應的展開式進行比較，從而確定假設的傳遞函數的各項數。

假設各個擾動下的傳遞函數為

2017年，IPO審核加速帶動了創投基金的募集、投資和退出，政府引導基金的進一步擴容引導了社會資金更多地流進創投基金和實體經濟，港股、美股的窗口期為具有國際視野的創投基金帶來更大的機會，整個中國創投行業呈現出良好的發展態勢。無疑，創投行業的快速發展，已經成為破解中小企業“融資難”問題、加快金融供給側改革的重要手段。

對于電池板初始溫度擾動，將式(6)與式(9)均在s=0 點處展開泰勒級數，取其前三項相等得到式(9)的系數分別為:，T。指數n 總是四舍五入取整數。

對于太陽光照強度G 擾動，將式(7)與式(9)均在s=0 點處展開泰勒級數，取其前三項相等得到(9)式的系數的系數分別為:K=。指數n 總是四舍五入取整數。

對于水工質流量d 擾動，將式(8)與式(9)均在s=0 點處展開泰勒級數，取其前三項相等得到式(9)的系數分別為:，n=2，T。指數n 總是四舍五入取整數。

1.2 集總參數建模法

水的能量平衡:

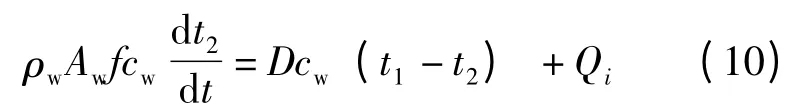
式中:Qi為水與電池板之間的換熱量;t1，t2分別為水的進出口溫度。

電池板對水的放熱量:

式中:tc為電池板的溫度。

電池板的能量平衡方程:

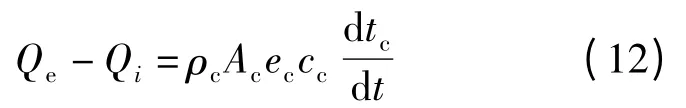
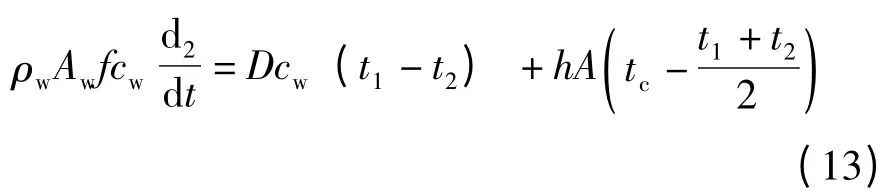
由式(2)、(11)、(12)可得:

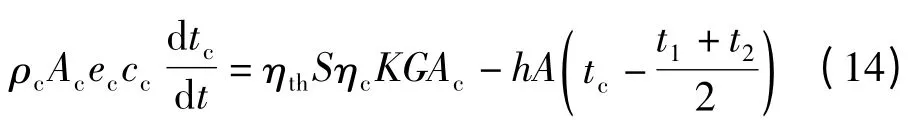
對上述式(13)、(14)分別作拉氏變換，經推導得溫度、流量和光照強度擾動的傳遞函數模型:

電池板初始溫度擾動:

水工質流量D 擾動:

太陽光照強度G 擾動:

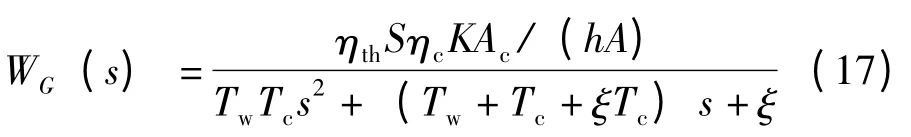
2 模型仿真與分析

根據表1 中的原始數據和簡化結果得到分布參數模型在各個擾動下的傳遞函數為:

表1 參數物理意義

電池板初始溫度擾動:

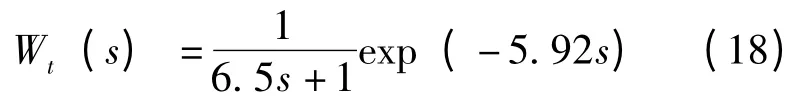
太陽光照強度擾動:

水工質流量擾動:

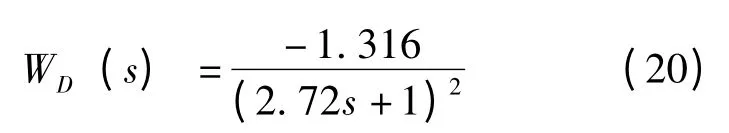
根據表1 中的原始數據和式(15)～(17)得到集總參數模型在各個擾動下的傳遞函數為:

電池板初始溫度擾動:

太陽光照強度擾動:

水工質流量擾動:

求取以上各傳遞函數的階躍響應曲線，如圖3，4，5 所示，(a)圖均為分布參數模型，(b)圖均為集總參數模型。由圖3 可以看出，當光照強度增加1 W/m2，電池板的溫度大約增加0．024 K;由圖4 可以看出，當流體流量增加1 kg/s，其他擾動為零時，電池板溫度下降大約1．35 K;由圖5 可以看出，當電池板初始溫度增加1 K，其他擾動為零時，電池板最終溫度在一定的時間范圍內上升1 K。綜上，當光照強度增加時電池板的溫度會升高。當流體的質量流量增加時，會帶走更多的熱量，從而電池板的溫度會有所下降，由此可判斷流量越快，電池板降溫越快。當電池板的初始溫度發生變化的時候電池板的最終溫度會變化相同的幅度。對比分布參數模型和集總參數模型的曲線可以看出分布參數模型能更好地反映系統的動態性能，但是分布參數法計算復雜。

圖3 電池板溫度在光照強度擾動下的響應

圖4 電池板溫度在流體流量擾動下的響應

圖5 電池板溫度在初始溫度擾動下的響應

3 結論

通過對復合拋物面聚光器(CPC)型太陽能光伏/光熱聯合利用(PV/T)系統生產工藝的研究，本文利用能量守恒定律得出了PV/T 系統的分布參數模型和集總參數模型，分別給出了在不同擾動下電池板溫度的傳遞函數，并且進行了仿真。仿真結果表明，這兩種機理建模方法都能夠很好地反映系統的動態性能。由模型可以看出，流體流量是控制電池板溫度在最佳工作點的主要因素。機理模型的確定為CPC-PV/T 系統的進一步優化奠定了理論依據，為CPC-PV/T 系統控制算法的研究提供了技術支撐。

［1］魏進家，謝胡凌，敬登偉．一種太陽能聚光分頻光伏光熱聯產裝置［P］．中國專利．CN201210224815．9，2012．

［2］劉亞雷，張紅，許輝，等．CPC 型聚光光伏光熱系統的性能分析［J］．可再生能源，2011，29(1):1-5．

［3］崔文智，于松強，廖全．聚光型混合光伏光熱系統熱電性能分析［J］．重慶大學學報，2009，32(1):86-90．

［4］孫健，王艷香，施明恒．復合拋物面聚光太陽能PV/T 系統的實驗研究［J］．太陽能學報，2012，33(1):86-91．

［5］Amrizal N，Chemisana D，Rosell J I．Hybrid photovoltaic-thermal solar collectors dynamic modeling［J］．Applied Energy，2013，101:797-807．

［6］Mohd Yusof Hj Othman，Baharudin Yatim，Kamaruzzaman Sopian，et al．Performance analysis of a double-pass photovoltaic/thermal(PV/T)solar collector with CPC and fins［J］．Renewable Energy，2005，30(13):2005-2017．

［7］韓璞，董澤，王東風，等．智能控制理論及應用［M］．北京:中國電力出版社，2012．

［8］李雅哲，塔式太陽能熱發電蒸汽系統建模與控制［D］．北京:華北電力大學，2011．

［9］馬進，劉長良，李淑娜．穩壓器壓力水位控制系統建模與仿真［J］．核科學與工程，2010，30(1):9-14．

［10］康英偉，薛陽，黃偉．電站鍋爐過熱器的集總參數動態建模與仿真［J］．計算機仿真，2012，29(9):332-334．

［11］阮剛，羅自學，周懷春．鍋爐過熱蒸汽溫度控制新策略動態仿真研究［J］．華中電力，2004，17(5):1-4．

［12］周少祥，胡三高，宋之平．管式換熱器分布參數模型的分段線性化方法研究［J］．中國電機工程學報，2002，22(6):123-125．

［13］李旭．蒸汽發生器的動態特性——模型、結構參數的影響和控制［D］．北京:清華大學，1988．

［14］倪維斗，徐向東，李政，等．熱動力系統建模與控制的若干問題［M］．北京:科學出版社，1996．

［15］(美)E0．道別林，童鈞芳．系統的建模和響應—理論及實驗方法［M］．關國樞譯．上海:科學技術文獻出版社，1984．