關于不定方程組x±1=6pqu2，x2?x+1=3υ2 的整數解

杜先存， 孫映成， 萬 飛

(1．紅河學院 教師教育學院 云南蒙自661199;2．鹽城師范學院數學科學學院 江蘇鹽城224002)

0 引言

關于三次不定方程

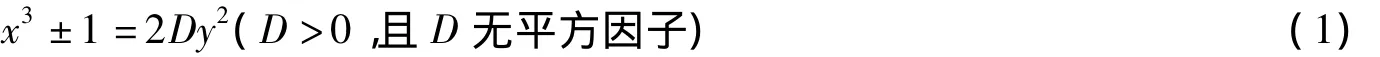
的整數解的問題一直是數論研究者關注的問題．文獻［1－5］給出了一些結果．

就起著重要的作用．然而關于不定方程組(2)的整數解的情況，目前僅就D為素數時，有一些結論:文獻［6］得出了方程組x+1=6Du2，x2－x+1=3v2無正整數解;文獻［7］得出了x－1=6Du2，x2+x+1=3v2僅有整數解(D，x，u，v)=(D，1，0，±1)，(13，313，±2，±181)．

本文將利用遞歸序列、Pell方程的解的性質、Maple小程序，得出當D含兩個互異的6k+1型素因子時方程組(2)的解的情況．

1 主要引理

引理1［8］設p是一個奇素數，則丟番圖方程4x4－py2=1除開p=3，x=y=1和p=7，x=2，y=3外，無其他的正整數解．

引理2［8］方程 x2－3y4=1 僅有整數解

2 主要定理及證明

定理1 設p，q為互異的奇素數，p≡q≡1(mod 6)，則不定方程組

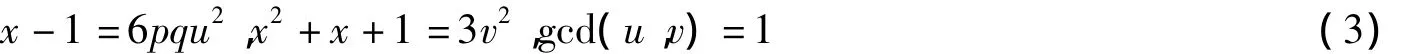
只有平凡解(x，u，v)=(1，0，±1)．

證明 1)先證存在性

將式(3)的x=1+6pqu2代入x2+x+1=3v2，整理得

設(xn，yn)(n∈Z)為Pell方程X2－3Y2=1的任意整數解，顯然 2 +是Pell方程X2－3Y2=1的基本解．于是式(4)的一切整數解可表示為

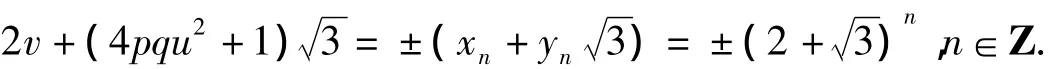
因此，4pqu2+1= ±yn(n∈Z)，即4pqu2= ±yn－1．又 y－n= －yn，所以只需考慮

由式(5)，得 yn≡1(mod 4)．

容易驗證下列各式成立:

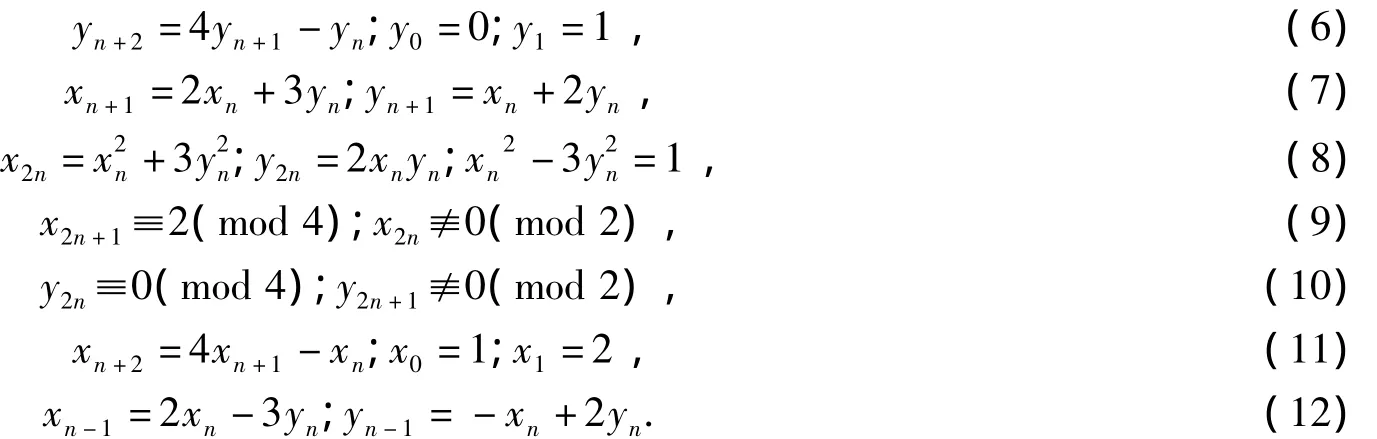
對遞歸序列(6)取模4，得周期為4的剩余類序列，且僅當n≡1(mod 4)時，有yn≡1(mod 4)，所以只有當n≡1(mod 4)時式(5)才成立．

當 n≡1(mod 4)時，不妨令 n=4m+1(m∈Z)，則由式(5)、(7)和(8)得

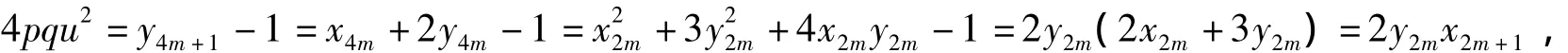
即2pqu2=x2m+1y2m．

由式(7)得，gcd(x2m+1，y2m)=gcd(2x2m+3y2m，y2m)=gcd(2x2m，y2m)=gcd(2，y2m)=2．又由式(9)、(10)得，x2m+1≡2(mod 4)，y2m≡0(mod 4)，所以下列情形之一成立:

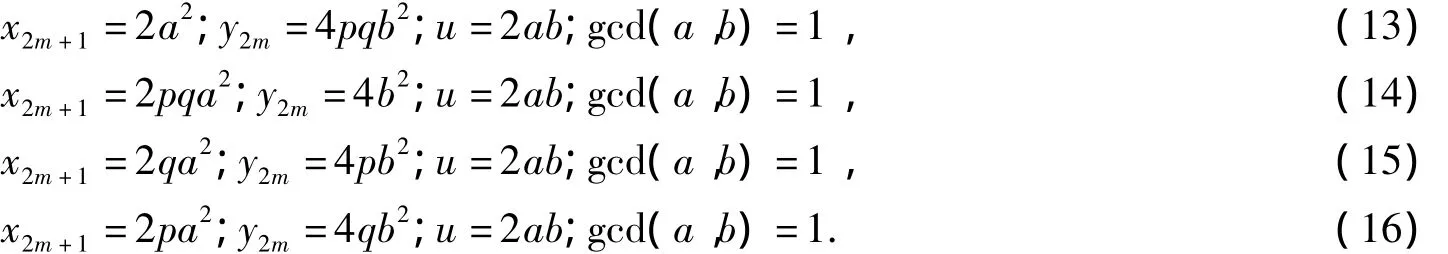
將式(13)中x2m+1=2a2代入x22m+1－3y22m+1=1，得4a4－3y22m+1=1．根據引理1知，a= ±1，此時x2m+1=2，則 m=0．再由式(6)得 y0=0，故由式(13)中 y2m=4pqb2，得 4pqb2=0，則 b=0，故 u=0，于是得到方程組(3)的平凡解(x，u，v)=(1，0，±1)．

2)再證唯一性

由式(14)的 y2m=4b2得 xmym=2b2，又由式(10)知 ym?2(mod 4)，而 gcd(xm，ym)=1，故 xm=2c2，ym=d2，因此有4c4－3y2m=1．根據引理1 知，c= ±1，ym= ±1．則由 c= ±1 得，xm=2，故 m=1．此時由式(11)得x3=26，故由式(14)的 x2m+1=2pqa2，得26=2pqa2，所以 a=1，pq=13，這與“p，q為互異的奇素數”矛盾．所以該情形方程組(3)無整數解．

由式(15)的y2m=4pb2得xmym=2pb2，又由式(10)知ym?2(mod 4)，而 gcd(xm，ym)=1，所以下列情形之一成立:

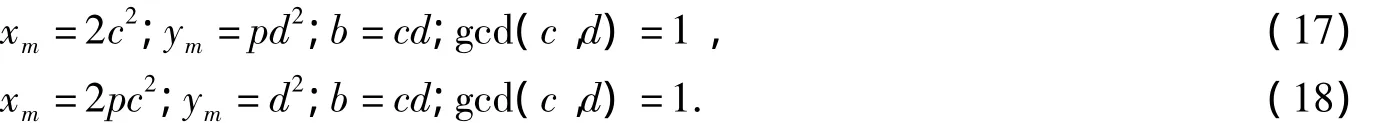
若式(17)成立，則有4c4－3y2m=1．由引理1 知，ym= ±1，則由式(18)ym=pd2，得1=pd2，則有p=1，這與“p為奇素數”矛盾，所以該情形方程組(3)無整數解．

若式(18)成立，則有 x2m－3d4=1．由引理2 知，xm= ±1，±2，±7，故由式(18)xm=2pc2，有 2pc2=2，則p=1，這與“p為奇素數”矛盾，所以該情形方程組(3)無整數解．

由式(16)的y2m=4qb2，仿式(15)的討論知，該情形方程組(3)無整數解．

綜上1)和2)可知，定理1成立．

從2018年初開始，合作社不再聘請執行理事，所有經營管理由村兩委負責。合作社每年將召開全體成員大會一次，向全體社員匯報年度的重要工作、財務收支、股權分紅以及下一年度工作計劃。

定理2 設p，q為互異的奇素數，p≡q≡1(mod 6)，則不定方程組

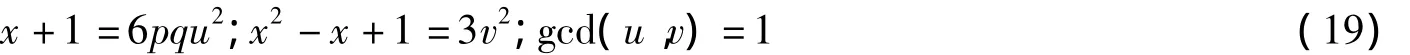
僅有平凡解(x，u，v)=(－1，0，±1)．

事實上，將x=6pqu2－1代入x2－x+1=3v2，整理得

仿照定理1的證明可知式(20)的一切整數解可表示為

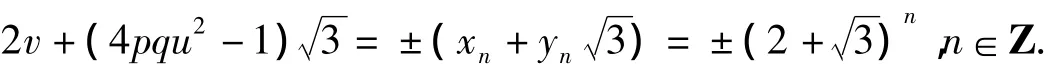
為此也只需考慮

由式(21)，得 yn≡ －1(mod 4)．

對遞歸序列(6)取模4，得周期為4的剩余類序列，且僅當n≡－1(mod 4)時，有yn≡－1(mod 4)，所以只有當n≡－1(mod 4)時式(21)才成立．

當 n≡ －1(mod 4)，令 n=4m －1(m∈Z)，則由(8)、(12)和(21)得

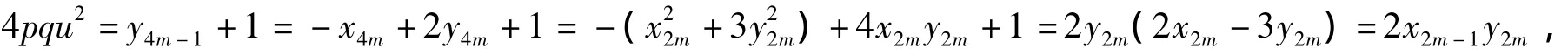
即

由式(6)知僅當m=0時，y2m=0．又由式(11)知對于任意整數m，均有x2m－1≠0，所以僅當 m=0時，x2m－1y2m=0．

(i)m=0 時，由式(22)得，u=0，此時得出方程組(19)的平凡解(x，u，v)=(－1，0，±1)．

(ii)m≠0時，仿定理1的證明可知不定方程組(19)無整數解．

綜上，定理成立．

對于方程組(2)的整數解的情況，本文僅僅給出了D含兩個互異的6k+1形素因子時的解的情況，對于D含3個及以上互異的6k+1形素因子時方程組(2)的解的情況還有待于進一步研究．

［1］ 柯召，孫琦．關于丟番圖方程 x3±1=Dy2［J］．中國科學，1981，24(12):1453 －1457．

［2］ 黃壽生．關于指數 Diophantine方程 x3－1=2py2［J］．數學研究與評論，2007，27(3):664 －666．

［3］ 管訓貴．關于 Diophantine方程x3±1=2py2［J］．云南民族大學學報:自然科學版，2012，21(6):438 －441．

［4］ 張海燕，王連芳．關于丟番圖方程x3±1=2Dy2［J］．哈爾濱理工大學學報:自然科學版，1997，2(6):85 －87．

［5］ 杜先存，趙東晉，趙金娥．關于不定方程x3±1=2py2［J］．曲阜師范大學學報:自然科學版，2013，39(1):42－43．

［6］ 田曉霞．關于不定方程組 x+1=6py2，x2－x+1=3z2［J］．四川理工學院學報，2009，22(1):30 －31．

［7］ 牟全武．對文“關于指數Diophantine方程x3－1=2py2”的注記［J］．西安文理學院學報:自然科學版，2008，11(4):43 －45．

［8］ 曹珍富．丟番圖方程引論［M］．哈爾濱:哈爾濱工業大學出版社，1989．