改進的分水嶺算法在圖像分割中的研究

王改云，楊小娟

（桂林電子科技大學 電子工程與自動化學院，廣西 桂林 541004）

圖像分割是計算機視覺研究中的一個極為重要的基本問題，是由圖像處理到圖像分析的關鍵步驟“分割結果的優劣直接影響到隨后的圖像分析!理解和景物恢復問題求解的正確與否”圖像分割技術的發展與許多其它學科密切相關，例如電子學，計算機科學，醫學，數學等學科等隨著各學科新理論和新方法的提出，人們也提出了許多結合一些特定理論方法和工具的分割技術[1]。

雖然目前上千種圖像分割算法但還沒有一種普適性方法來解決所有圖像分割問題，而且迄今為止，也沒有一種完善的理論來指導如何根據圖像特點來選擇合適的分割方法。國內外學者在對圖像分割方法的不斷研究中，主要將傳統圖像分割方法進行不斷的改進，以及結合新理論新概念研究出新的可行的分割方法[2]。

經過研究發現目前普遍的分水嶺算法存在如下缺點：1）對圖像中的噪聲極敏感，輸入圖像通常是圖像梯度，而原始圖像中的噪聲能直接惡化圖像的梯度，易于造成分割輪廓偏移；2）易于產生過分割。由于受噪聲、量化誤差以及區域內紋理細節的影響，因此會產生很多局部最小值，在后續分割中將出現大量細小區域；3）對低對比度圖像易丟失重要輪廓。在此情況下，區域邊界像素的梯度值也較低，那么目標的重要輪廓容易丟失[8]。

基于分水嶺算法的圖像分割逐漸受到了人們重視，它是幾年發展起來的形態學分割方法，它的分割思想至今仍是廣大學者關注的研究熱點，在圖像分割方法中占有一席之地。

1 分水嶺算法

分水嶺分割方法是近些年被人們廣泛應用的一種基于拓撲理論的數學形態學的分割方法，基本思想是把圖像看作是測地學上的拓撲地貌，圖像中每一點像素的灰度值表示該點的海拔高度，每一個局部極小值及其影響區域稱為集水盆，而集水盆的邊界則形成分水嶺。分水嶺的概念和形成可以通過模擬浸入過程來說明。在每一個局部極小值表面，刺穿一個小孔，然后把整個模型慢慢浸入水中，隨著浸入的加深，每一個局部極小值的影響域慢慢向外擴展，在2個集水盆匯合處構筑大壩，即形成分水嶺。分水嶺的計算過程是一個迭代標注過程，比較經典的計算方法是L.Vincent提出的。分水嶺算法包含排序和浸水2個過程，其中排序過程按照像素的灰度進行排序，以便直接訪問同一高度的像素：在浸水過程中，假設高度小于等于h的像素的貯水盆地已經標記出來了，則在處理高度為h+1的像素時，將這一層中與已標記的貯水盆地相鄰的像素送入先入先出隊列，再由這些像素開始，根據測地距離,將已經標記的貯水盆地擴展至h+1層；然后，通過掃描，將h+1層中可能存在的區域最小值賦予新的標號；最后，在分水嶺變換的結果中，同一標號的像素屬于同一貯水盆地,而將距不同貯水盆地距離相等的像素標為分水嶺點。分水嶺變換得到的是輸入圖像的集水盆圖像，貯水盆之間的邊界點，即為分水嶺[3]。

顯然，分水嶺表示的是輸入圖像極大值點。因此，為得到圖像的邊緣信息，通常把梯度圖像作為輸入圖像，即數學表達如下：

式中，f（x，y）表示原始圖像，grad（，）表示梯度運算。

令 M1，M2，…，MR 為表示圖像 g（x，y）的局部最小值點的坐標的集合。令G（Mi）為一個點的坐標的集合，這些點位于與局部最小值Mi（回想無論哪一個匯水盆地內的點都組成一個連通分量）相聯系的匯水盆地內。符號min和max代表g（x，y）的最小值和最大值。最后，令 T[n]表示坐標（s，t）的集合，其中 g（s，t）＜n，即

在幾何上，T[n]是 g（x，y）中的點的坐標集合，集合中的點均位于平面g（x，y）=n的下方。隨著水位以整數量從n=min+1到n=max+1不斷增加，圖像中的地形會被水漫過。在水位漫過地形的過程中的每一階段，算法都需要知道處在水位之下的點的數目。從概念上來說，假設T[n]中的坐標處在g（x，y）=n平面之下，并被“標記”為黑色，所有其他的坐標被標記為白色。然后，當我們在水位以任意增量n增加的時候，從上向下觀察xy平面，會看到一幅二值圖像。在圖像中黑色點對應于函數中低于平面g（x，y）=n的點。這種解釋對于理解下面的討論很有幫助。

令Cn（Mi）表示匯水盆地中點的坐標的集合。這個盆地與在第n階段被淹沒的最小值有關。參考前一段的討論，Cn（Mi）也可以被看做由下式給出的二值圖像：

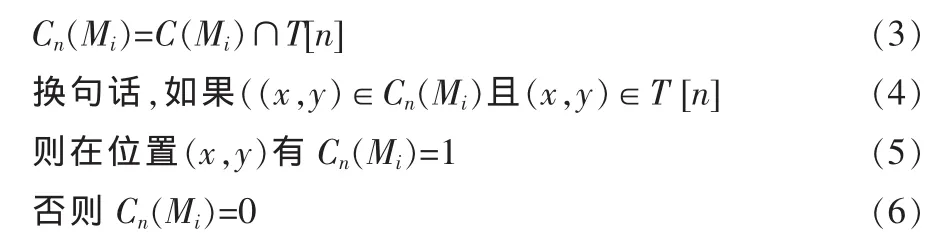
對于這個結果幾何上的解釋是很簡單的。只需在水溢出的第n個階段使用“與(AND)”算子將T[n]中的二直圖像分離出來即可。T[n]是與局部最小值Mi相聯系的集合。接下來，令C[n]表示在第n個階段匯水盆地被水淹沒的部分的合集：

然后令C[max+1]為所有匯水盆地的合集：

可以看出處于Cn（Mi）和T[n]中的元素在算法執行期間是不會被替換的，而且這2個集合中的元素的數目與n保持同步增長。因此，C[n-1]是集合C[n]的子集。C[n]是T[n]的子集，所以，C[n-1]是T[n]的子集。從這個結論得出重要的結果：C[n-1]中的每個連通分量都恰好是T[n]的一個連通分量。

找尋分水線的算法開始時設定C[min+1]=T[min+1] （9）

然后算法進入遞歸調用，假設在第n步時，已經構造了C[n-1]。根據C[n-1]求得C[n]的過程如下：令Q代表T[n]中連通分量的集合。然后，對于每個連通分量q∈Q[n]，有下列3種可能性：

根據C［n-1］構造C［n］]取決于這3個條件。當遇到一個新的最小值時符合條件（a），則將 q 并人 C［n-1］構成 C［n］。當q位于某些局部最小值構成的匯水盆地中時，符合條件（b），此時將 q 合并入 C［n-1］構成 C［n］。 當遇到全部或部分分離2個或更多匯水盆地的山脊線的時候，符合條件（c）。進一步的注水會導致不同盆地的水聚合在一起，從而使水位趨于一致。因此，必須在q內建立一座水壩（如果涉及多個盆地就要建立多座水壩）以阻止盆地內的水溢出。正如前一節中的解釋，當用3×3個1的結構元素膨脹q∩C[n-1]并且需要將這種膨脹限制在q內時，一條一個像素寬度的水壩是能夠構造出來的。通過使用與g（x，y）中存在的灰度級值相對應的n值，可以改善算法效率；根據g（x，y）的直方圖，可以確定這些值及其最小值和最大值[4]。

此次研究是基于數學形態學的分割算法，在對圖像去噪的前提下進行分水嶺圖像分割方法處理，可以比較有效的消除過分割現象。

2 仿 真

本文中以土豆圖像為例，該圖像中多個對象相連,我們所要達到的目的就是在圖像分割后被分割成多個獨立對象,由于選取的圖片本身比較模糊，要先進行處理，原圖如圖1所示。

圖1 原始圖像Fig.1 Original image

圖2 經過預處理的對比圖Fig.2 After comparing the graph preprocessing

中值濾波效果較好，經過中值濾波后原先模糊的圖片可以變得更清晰，方便后續處理。如圖3運用巴特沃斯低通濾波和中值濾波，接下來利用函數Info=im finfo（filename）；

從圖3看到形象生動的原始分水嶺圖像和中值濾波處理后的分水嶺圖像，接下來構造結構元素（Structuring element），用分水嶺來增強圖像中感興趣的對象，結構元素就是好比是一張小圖像，通常用于圖像的形態學運算（如膨脹、腐蝕、開運算、閉運算）[5]。在此次研究中，先設置參數，創建se=stel（‘disk,40）結構，再對去噪后圖像進行銳化增強，并且用bottom-hat來增強圖像對比度。利用Itop函數處理如圖4所示。

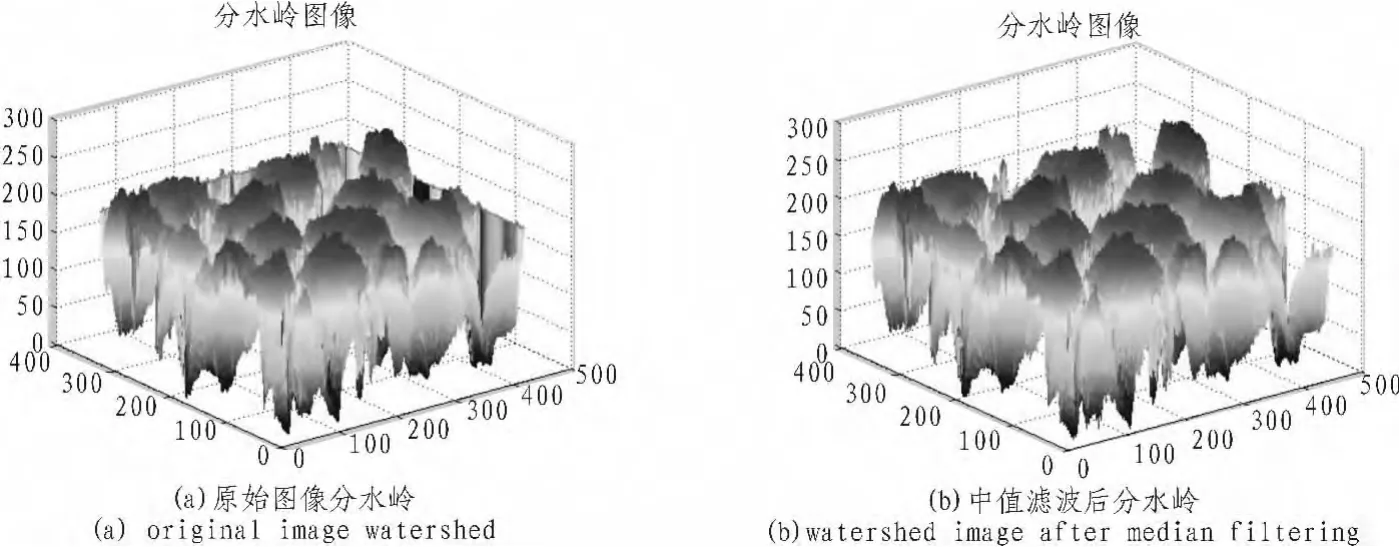
圖3 分水嶺對比圖Fig.3 Comparison chart ofWatershed

圖4 增強處理Fig.4 Enhancement

可是會從圖4發現，對象間隙比較緊密，為了達到更好分割效果，我們要增大間隙，還要再用imcomplement函數增強圖像中感興趣對象。

圖5 增大間隙和感興趣對象Fig.5 Increase the gap and the objectof interest

由圖5（a）發現圖像對象間隙明顯增大，較好的達到了預期效果。再利用rgb函數所得分水嶺如圖7所示。

圖6 temin圖和rag分水嶺圖Fig.6 temin image and ragerwater image

圖7 濾波前后對比圖Fig.7 Filter before and after comparison chart

由圖7可以看出經過上述一系列處理后分割的更清楚，而且分水嶺分割會將本來連在一起的圖像分開成單獨的圖像，達到較為理想的效果。

3 結束語

為了克服傳統分水嶺算法的缺點，已經有很多學者努力進行了相關研究，并且提出了一些改進型分水嶺算法，并成功應用到相關應用領域。例如一些將分水嶺算法與其他方法相融合，為解決項目中遇到的實際問題提供了思路。不過因為在初始分割時盡量抑制噪聲和細密紋理的影響，同時還要保留重要輪廓，這將成為解決傳統分水嶺算法問題的根本途徑，相信隨著人們的不斷深入探索和進一步研究，會出現更多更好更有效的解決方法。

[1]王鳳娥.改進后的分水嶺算法在圖象分割中的應用研究[D].濟南：山東大學，2008.

[2]徐琳俊.數字圖像分割算法研究[D].濟南:山東大學，2013.

[3]徐偉，王希常，鄭志寬.一種基于改進分水嶺算法的圖像分割算法[J].計算機技術與發展，2008，18（12）:38-40.XU Wei， WANG Xi-chang， ZHENG Zhi-kuan.A segmentation algorithm for image based on improved watershed algorithm[J]. Computer Technology and Development，2008，18（12）:38-40.

[4]Rafael C.Gonzalez.Richard E.Woods數字圖像處理[M].北京：電子工業出版社，2011.

[5]唐曉強，賴惠成.形態學結構元素選取算法的研究[J].通信技術，2010，223（7）：161-162.TANGXiao-qiang，LAIHui-cheng.Research on communication technology of[J].algorithm selects the structure element of mathematicalmorphology，2010，223（7）:161-162.

[6]羅勇.改進后的分水嶺算法在圖象分割中的應用研究[D].哈爾濱：哈爾濱工業大學，2003.

[7]YongRui，HuangTS.Content-Based Image Retrieval with Relevance FeedbackinMARs[J].ICIP， 1997，2:815-818.

[8]刁智華，趙春江.分水嶺算法的改進研究[J].計算機工程，2010，36（17）:10-12.DIAO Zhi-hua，ZHAO Chun-jiang.Study on the improvement ofwatershed algorithm[J].Computer Engineering， 2010， 36（17）:10-12.

[9]岡薩雷斯.數字圖像處理（MATLAB版）[M].北京：電子工業出版社，2005.