淺談初中數學概念教學的六種方法

張明寧

【摘 要】 在教學過程中，通過生活實例引入概念法、理解為先掌握概念法、識記掌握概念法、比較掌握概念法、反復練習鞏固概念法、巧設問題引入概念法，把概念教學落到實處，讓學生清晰地掌握數學概念。

【關 鍵 詞】 概念教學；識記比較；導入練習

在現在的新教材里，數學概念已占據了較多的內容，大部分教師在教學過程中，只注意知識的傳授，而忽視了對學生思維能力的培養和整體素質的提高。概念是數學思維的細胞，數學概念是數學基礎知識的重要組成部分，是學習數學知識的基石。在過去的一段時間里，教師上課時始終圍繞例題講述，采取“零售”數學知識的辦法，把數學概念當作“齊讀或勾畫”來處理，沒有發揮概念教學的優勢，在各種題型的練習中，以題海戰術為重點，而老師也整天在題庫里忙忙碌碌的鉆研，學生也同時昏昏欲睡的被埋到解題中。而事實證明：只要求學生學會解題，而不給學生講透實質問題；只給學生一把對號開鎖的鑰匙，而不給學生講解剖鎖的結構原理。因此，我認為在教學過程中，首先應進行概念教學，使學生掌握系統的數學知識，透切理解數學概念的含義和重要性。

下面就結合教學實踐，談談我在數學概念教學中的一些做法與體會。

一、生活實例引入概念法

概念屬于理性認識，它的形成依賴于感性認識，學生的心理特點是容易接受和理解具體的感性認識的。教學過程中，各種形式的直觀教學是提供豐富、正確感性認識的主要途徑。所以在講述新概念時，除引導學生觀察和分析有關具體實物外，同時告訴概念的本質和特征。如一段鐵路上兩條筆直的鐵軌可作為平行線的原型，人字架屋頂可作為等腰三角形的原型，溫度計作為數軸的原型，正方形的對角線的長度與其一邊的比可作為無理數的原型。在講解“梯形”的概念時，我結合學生的生活實際，引入梯形的典型實例（如梯子、堤壩的橫截面等），再畫出梯形的標準圖形，讓學生獲得梯形的感性知識。再如，講“數軸”的概念時，我模仿秤桿上用點表示物體的重量。秤桿具有三個要素：①度量的起點；②度量的單位；③明確增減方向，這樣以實物啟發人們用直線上的點表示數，從而引出數軸的概念。（規定了原點、正方向和單位長度的直線叫做數軸）。這種形象的講述符合認識規律，學生容易理解，給學生留下的印象也較為深刻。

二、理解為先掌握概念法

概念的理解是概念教學的中心環節，概念的獲得是學生經過分析、綜合、比較、抽象概括的結果。在每個概念導入后，教師應認真剖析，在剖析的過程中讓學生理解并掌握概念的本質。如對“正弦”函數進行剖析，它涉及到比的定義、角的大小、相似三角形、函數概念等知識，正弦的值本質上是一個“比值”。為突出這個本質，可引導學生思考：正弦是一個比，這個比是？∠A的對邊與斜邊的比值；這個比值隨∠A大小的確定而確定，與∠A的對邊與斜邊的長度無關；由于是對邊與斜邊的比，所以這個比值不超過1。經過對正弦概念的本質屬性分析后指出：直角三角函數只有六個，這便是三角函數的外延，在初中我們僅學習了其中三個（正弦、余弦，正切）。

三、識記掌握概念法

目前，在教學中有一種錯誤的觀點認為，素質教育就可以削弱學生記憶背誦的部分。其實如果不通過有效的背誦記憶，概念雖然理解了，若不能完整的記憶，則仍無法掌握。英國科學家培根曾說：“一切知識莫過是記憶，而創造不可是運用知識。”由此可見，在學習中記憶是不可缺少的重要過程。如前面提到的正弦的概念，雖然理解了其中的核心項內容，但如果不及時加以牢記，遇到問題的時候仍會抓不住問題的本質，造成答非所問、句不達意。當然，記憶的過程應建立在充分理解的基礎上，理解和記憶是相互促進和制約的，切不可偏一而為。所以在教學過程中，必須給學生記憶概念的時間。

四、比較掌握概念法

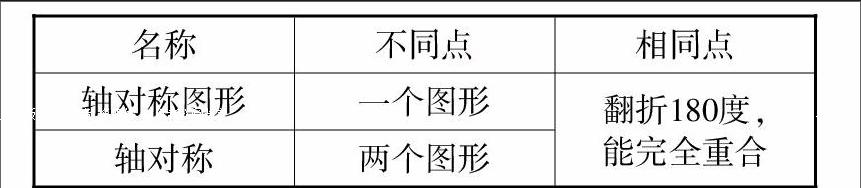
要牢固地記住一些基本概念，適當的比較是不可缺少的。有比較才有鑒別，數學的各種知識應讓學生在比較中去思考、去認識。數學的一些概念和規律，理論性較強而且比較抽象。如果把它與學生熟悉的（已知的）相關實體（事物）進行比較，可以幫助學生找出其特點，如它相同點、不同點。由其特點來進行分析、比較，使學習的記憶過程得到強化。如關于“軸對稱”和“軸對稱圖形”兩個概念，學生較難理解，可以讓他們觀察常見的汽車標志（如大眾、桑塔納）或商標等，發現它們的共同特性：沿某條直線翻折，直線左右兩旁能完全重合，這樣學生就容易理解軸對稱概念。同樣，可以讓學生觀察中國民間剪紙、窗紙、人的兩只手等，便可發現：一個圖形沿某條直線翻折，能與另一個圖形完全重合，得到“兩個圖形成軸對稱”。于是有：

[名稱＼&不同點＼&相同點＼&軸對稱圖形＼&一個圖形＼&翻折180度，

能完全重合＼&軸對稱＼&兩個圖形＼&]

反過來，如果把一個軸對稱圖形，對稱軸兩旁的部分分別看成兩個圖形，那么它們成軸對稱，把兩個成軸對稱的圖形看成一個圖形，那么它就成了軸對稱圖形，這樣學生對成“軸對稱”和“軸對稱圖形”兩個概念就得到了透徹的理解。

五、反復練習鞏固概念法

要想使所學知識消化吸收，鞏固應用自如。首先，應在初步形成概念后，引導學生正確復述概念；其次，要運用變式加深理解，在此過程中培養學生的應用能力。特別是一些抽象的基本概念，更應從不同角度去練習掌握。

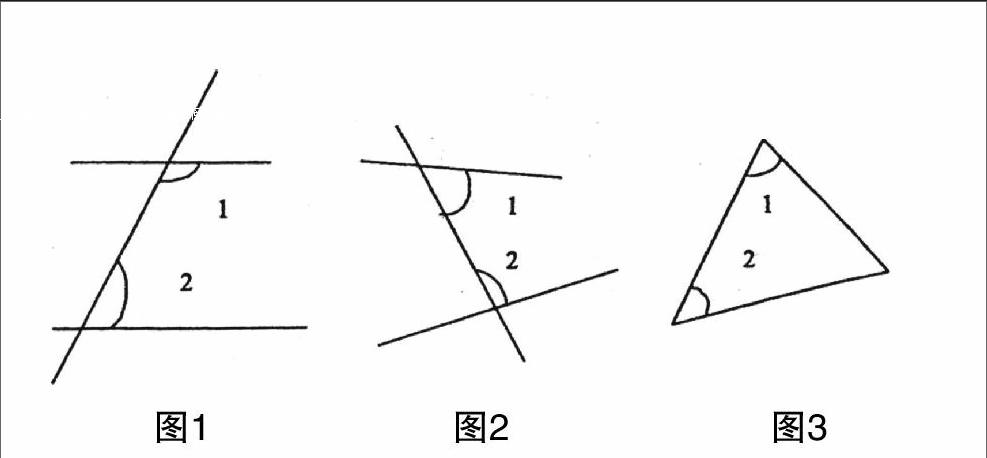
如為了幫助學生認識“同旁內角”的本質特征。教師可以提供一組“形變而質不變”的感性材料：

然后讓學生分析圖中的1、2是什么位置關系的角，這樣學生不但能找出標準圖形（圖1）中的同旁內角，進而能有效地排除變式的干擾，對概念的理解更加深刻。

[圖1 圖2 圖3]

如果經常進行有關概念的練習，就可以使基本概念在學生的練習中得到強化，并熟練每個概念在不同條件下的應用和適用范圍，真正懂得概念的深度和廣度。

六、巧設問題引入概念法

在數學概念的教學中，教師可創設一系列小問題，制造認知沖突，使學生感到所面臨的問題是熟悉的、常見的，同時又是新奇的、富有挑戰性的，使這些連續的階段問題能持續地激發學生的學習熱情和探索知識的興趣，促使學生情緒達到最佳境界。如教學“方程”這一概念時，設置了如下問題：①怎樣才能使天平保持平衡？②天平保持平衡說明了什么？③你能用式子來表示天平左邊和右邊重量的關系嗎？④式子中能不能含有求知數？⑤如果含有求知數，那么這種式子又稱為什么？這樣讓學生帶著問題操作天平、討論并解決以上問題，從而順利得出方程的概念。

對概念的理解絕不是簡單地要求學生死記硬背，而是讓學生在復述過程中把握概念的重點、要點、本質特征，同時注重應用概念的變式練習，恰當運用變式，能使思維不受消極定勢的束縛，實現思維方向的靈活轉換，使思維呈發散狀態。如在“有理數”與“無理數”的概念教學中，舉出“丌與3.14159”為例讓學生判斷，通過這樣的訓練，能有效地排除外在形式的干擾，對“有理數”與“無理數”的理解更加深刻。

“授之以魚，不如授之以漁”，教師只有平時重視對數學概念的教學，才能培養出學生的應變能力，才能讓學生建立起整個初中知識的結構圖，才能讓學生真正學會分析問題、比較問題和解決問題，才能讓學生從茫茫題海中解脫出來，也才能真正做到“快樂數學”！

【參考文獻】

[1] 趙順發. 淺談初中數學概念教學[J]. 學苑教育，2013（7）.

[2] 龔運勤. 數學課堂教學設計方法論[M]. 北京：北京理工大學出版社，2011.

[3] 黃先勇. 初中數學概念教學改革與探索[J]. 教育教學論壇，2013（33）.