一種基于最大信雜比的MTD濾波器設(shè)計算法

(中國電子科技集團(tuán)公司第三十八研究所,安徽合肥230088)

0 引言

在實際環(huán)境中,雷達(dá)接收信號不但含有來自運(yùn)動目標(biāo)的回波信號,也有從地物、云雨以及人為施放的箔條等物體散射產(chǎn)生的雜波信號。由于雜波往往比目標(biāo)信號強(qiáng)得多,雜波的存在會嚴(yán)重影響雷達(dá)對運(yùn)動目標(biāo)的檢測能力。因此,自適應(yīng)雜波抑制是雷達(dá)信號處理的重要內(nèi)容[1-4]。

在自適應(yīng)雜波抑制方法中,動目標(biāo)檢測(MTD)是一種利用多普勒濾波器來抑制各種雜波,以提高雷達(dá)在雜波背景下檢測運(yùn)動目標(biāo)能力的技術(shù)[1-4]。目前,MTD濾波器組常采用FFT濾波器組或有限脈沖響應(yīng)(FIR)濾波器組實現(xiàn)。與FFT濾波器組相比,FIR濾波器組中某些濾波器的(幅度)頻率響應(yīng)能夠在零頻附近靈活地形成較深的零陷,用于抑制零頻附近雜波。

對于FIR濾波器的設(shè)計,常規(guī)自適應(yīng)濾波器設(shè)計通常具有較高的旁瓣電平,抑制雜波的能力較差。為了降低旁瓣電平,可考慮加窗,如切比雪夫窗。加窗操作可以降低濾波器頻譜中旁瓣的衰減,但無法在零頻附近靈活地形成零陷。為了在零頻附近靈活地形成零陷,文獻(xiàn)[5]將空間陣列方向圖合成中的數(shù)字綜合算法[6]和常規(guī)自適應(yīng)濾波器相結(jié)合,討論了一種MTD濾波器設(shè)計算法。在該算法中,需要假設(shè)雜波的功率譜為高斯型,濾波器的初始頻率響應(yīng)旁瓣電平較高,濾波器系數(shù)求解需已知雜波的協(xié)方差矩陣,干擾功率需在整個濾波器頻譜的阻帶范圍內(nèi)調(diào)節(jié)。這些條件的限制會嚴(yán)重地影響算法的計算效率。

針對上述問題,本文直接借鑒文獻(xiàn)[6-7]中方向圖數(shù)字綜合算法的思想,提出了一種基于最大信雜比準(zhǔn)則的MTD濾波器設(shè)計算法。該算法直接將雜波建模為大量窄帶雜波的線性疊加,無需對雜波功率譜進(jìn)行假設(shè),濾波器的初始頻率響應(yīng)采用加窗處理,干擾功率僅需在零陷區(qū)域內(nèi)調(diào)節(jié)。與文獻(xiàn)[5]中算法相比,所提出的算法具有更快的收斂速度。

1 最大信雜比準(zhǔn)則

考慮N階FIR濾波器,其濾波器的系數(shù)向量可表示為

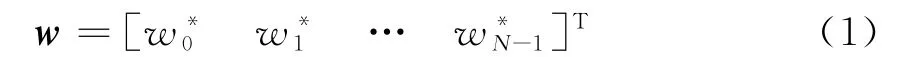
設(shè)FIR濾波器的各個抽頭組成的輸入向量為

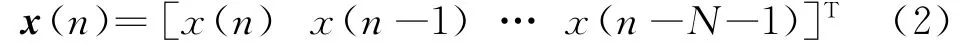
則FIR濾波器的輸出可表示為

在實際接收系統(tǒng)中,輸入信號是由期望信號、雜波和噪聲的線性疊加,即

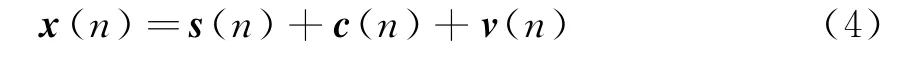
式中,s(n)為期望信號向量,c(n)和v(n)分別為雜波和噪聲向量。為了獲得最佳的FIR濾波器系數(shù),期望濾波輸出信號的信雜比最大,即使

達(dá)到最大。在公式中,Rs=E{s(n)sH(n)}為期望信號的自相關(guān)矩陣,Rcv是噪聲和雜波的自相關(guān)矩陣,它定義為

式中,Rc=E{c(n)cH(n)}為雜波的自相關(guān)矩陣,Rv=E{v(n)vH(n)}為噪聲的自相關(guān)矩陣。

若期望信號向量可表示為

式中,a為頻率向量,定義為

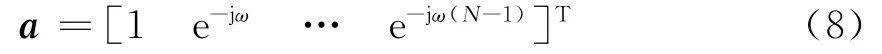
則由最大信雜比準(zhǔn)則獲得的最優(yōu)濾波器系數(shù)[8]為

式中,α為標(biāo)量,并不影響輸出的信雜比,在實際應(yīng)用中,通常取α=1。

2 MTD濾波器設(shè)計算法

基于信雜比準(zhǔn)則的MTD濾波器的設(shè)計思想是假設(shè)雜波由均勻分布在重頻范圍內(nèi)的許多窄帶雜波組成,調(diào)節(jié)各窄帶雜波的功率大小,使得濾波器系數(shù)在滿足期望阻帶衰減的同時,獲得最大的輸出信雜比。

設(shè)濾波器的期望阻帶衰減為D(ω)dB,則對應(yīng)的實際值為d(ω)=10D(ω)/20。假設(shè)系統(tǒng)噪聲為白噪聲,M個窄帶雜波均勻分布在整個重頻范圍內(nèi),且通帶內(nèi)的窄帶雜波功率固定為0。則雜波和噪聲的自相關(guān)矩陣為

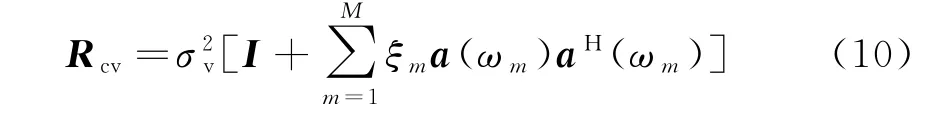
式中,σ2v為噪聲功率,實際應(yīng)用中,常取σ2v=1;ξm為第m窄帶雜波功率與噪聲功率的比值;ωm為第m窄帶雜波所在的中心頻率。為了使窄帶雜波不在各自中心頻率上獨(dú)立形成自適應(yīng)零陷,M應(yīng)取足夠大,一般建議取為濾波器自由度的2～3倍[6]。

窄帶雜波的功率調(diào)節(jié)的基本依據(jù)是,當(dāng)窄帶雜波位于濾波器通帶內(nèi)時,令其功率為零;當(dāng)濾波器的阻帶范圍內(nèi)某個頻點(diǎn)ωm處的衰減G(ωm)大于期望的阻帶衰減d(ωm)時,增加該頻點(diǎn)處的雜波功率;反之,減小該頻點(diǎn)處的雜波功率。如此不斷調(diào)節(jié),直到得到期望的阻帶衰減,最后一次調(diào)節(jié)對應(yīng)的自適應(yīng)權(quán)向量即為所求的最佳濾波器系數(shù)。

由于在每次調(diào)節(jié)后得到的濾波器通帶寬度會發(fā)生變化,而通帶內(nèi)不允許引入窄帶雜波,因此需要在每次調(diào)節(jié)時確定通帶的范圍,即確定頻譜第一零點(diǎn)ωL,ωH的位置,則通帶范圍為ωL≤ω≤ωH。另外,窄帶雜波功率不能為負(fù)數(shù),若在調(diào)節(jié)過程中,得到的阻帶區(qū)域內(nèi)雜波功率為負(fù),則令其等于零。

由以上分析可得,窄帶雜波功率由第k次到第k+1次調(diào)節(jié)時的更新公式

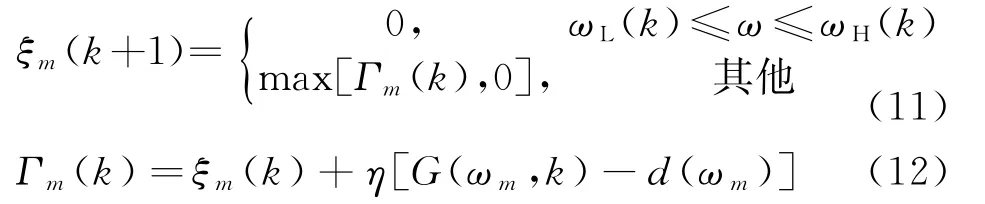
式中,η為調(diào)節(jié)因子,通常采用實驗獲得。第k次調(diào)節(jié)的濾波器系數(shù)為

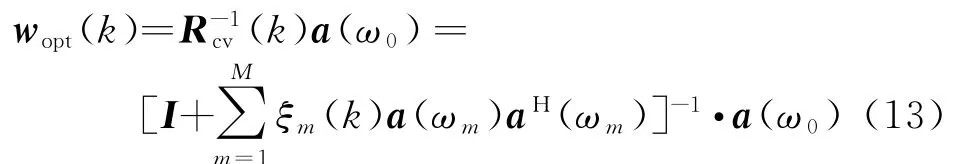
基于以上討論可得,基于信雜比準(zhǔn)則的MTD濾波器組的設(shè)計步驟如下：

步驟1 給定某個濾波器的中心頻率ω0,初始化濾波器系數(shù)初始化期望阻帶衰減d(ω)=10D(ω)/20和窄帶雜波功率ξm(0)=0,m=1,2,…,M,計算濾波器的初始通帶范圍ωL(k),ωH(k)。

步驟2 根據(jù)式(11)和(12)迭代調(diào)節(jié)窄帶雜波功率,根據(jù)式(13)計算最佳濾波器系數(shù),確定濾波器的通帶范圍ωL(k+1),ωH(k+1)。

步驟3 比較濾波器的實際阻帶衰減與期望阻帶衰減,若滿足要求,則停止;否則重復(fù)執(zhí)行步驟2。

值得注意的是,初始化的濾波器系數(shù)w(0)=a(ω0)對應(yīng)頻譜的第一旁瓣衰減為-13 dB,當(dāng)雷達(dá)系統(tǒng)要求M TD濾波器的阻帶衰減等波紋,且衰減較大時,算法所需的調(diào)節(jié)次數(shù)將增加。為了減少算法的調(diào)節(jié)次數(shù),一種方法是對初始濾波器系數(shù)進(jìn)行等波紋的切比雪夫加權(quán)。為了在零頻附近形成零陷,要求該權(quán)值對應(yīng)的阻帶衰減略大于期望阻帶衰減。當(dāng)對初始濾波器系數(shù)進(jìn)行加窗處理后,式(11)中窄帶雜波功率調(diào)節(jié)公式僅在零陷區(qū)域內(nèi)執(zhí)行,其他區(qū)域的窄帶雜波功率均等于零。

3 仿真實驗

本節(jié)將通過仿真實驗驗證所提算法的有效性。設(shè)MTD濾波器的階數(shù)為12,濾波器總個數(shù)為13,零頻附近4個濾波器的阻帶衰減-35 dB,剩余9個濾波器的阻帶衰減-35 d B,在零頻附近歸一化頻率寬度為0.05時零陷深度低于-60 dB。取調(diào)節(jié)因子為0.1,窄帶雜波個數(shù)為128,采用-40 d B的切比雪夫加權(quán)。

不同迭代次數(shù)時,歸一化中心頻率等于0.26的MTD濾波器的設(shè)計結(jié)果如圖1所示,其中圖中虛線是期望頻率響應(yīng),實線是利用所提方法設(shè)計出的MTD濾波器。圖1(a)是MTD濾波器的初始頻率響應(yīng),經(jīng)一次迭代處理的結(jié)果如圖1(b)所示。圖1(c)給出了3次迭代的結(jié)果,它滿足設(shè)計要求。在文獻(xiàn)[7]中給出了按式(14)初始化,通過迭代獲得等波紋的旁瓣電平的實例。在不產(chǎn)生零陷的情況下,該算法需要100次迭代才能滿足要求。由此可知,本文所提算法具有非常快的收斂速度。

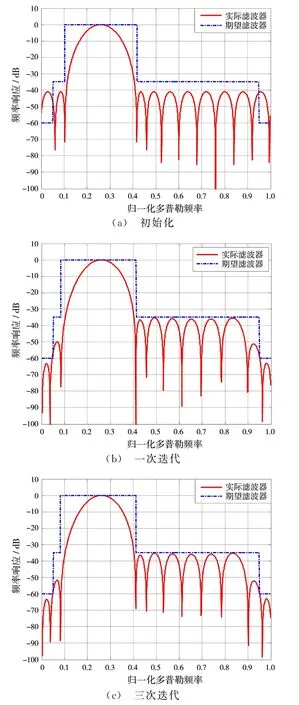
圖1 某一中心頻率處MTD濾波器的設(shè)計結(jié)果

對于零頻附近4個濾波器,令算法中窄帶雜波功率等于零,直接采用-35 dB的切比雪夫加權(quán)進(jìn)行設(shè)計。剩余9個濾波器采用本文算法進(jìn)行設(shè)計,使用-40 dB的切比雪夫加權(quán)。MTD濾波器組的設(shè)計結(jié)果如圖2所示。由圖可知,所提算法設(shè)計出的濾波器完全滿足要求。

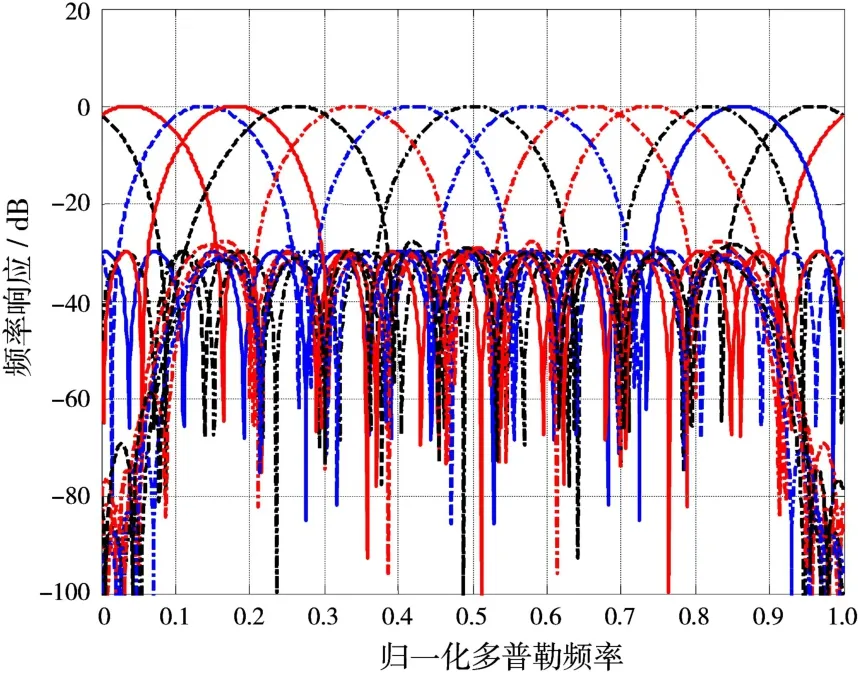
圖2 MTD濾波器組的設(shè)計結(jié)果

4 結(jié)束語

通過將接收雜波建模為大量均勻分布在重復(fù)頻率范圍內(nèi)的窄帶雜波信號的線性疊加,本文提出了一種新的MTD濾波器設(shè)計算法。該算法充分借鑒了陣列信號處理中自適應(yīng)陣列方向圖綜合的思想,利用期望頻響和實際頻響的差值控制窄帶雜波信號的功率強(qiáng)度,根據(jù)最大信雜比準(zhǔn)則獲得最佳濾波器系數(shù),具有較高的實用價值。值得注意的是,算法在窄帶雜波信號功率更新時,調(diào)節(jié)因子需根據(jù)頻率位置,通過實驗人工選擇,降低了設(shè)計MTD濾波器的效率。如何解決這一問題將是接下來的研究工作。

[1]吳順君,梅曉春.雷達(dá)信號處理和數(shù)據(jù)處理技術(shù)[M].北京：電子工業(yè)出版社,2008：105-146.

[2]SPAFFORD L J.Optimum Radar Signal in Clutter[J].IEEE Trans on Information Theory,1968,14(6)：734-743.

[3]陳小龍,關(guān)鍵,郭海燕,等.基于WPT-FRFT的微弱動目標(biāo)檢測及性能分析[J].雷達(dá)科學(xué)與技術(shù),2010,8(2)：139-145.

[4]D'ADDIIO E.Performance Comparison of Optimum and Conventional MTI and Doppler Processors[J].IEEE Trans on Aerospace and Electronic Systems,1984,20(6)：707-714.

[5]谷泓,趙永波,張守宏.一種基于數(shù)字綜合算法的MTD濾波器設(shè)計方法[J].航空計算技術(shù),2002,32(2)：58-62.

[6]OLEN C A,COMPTON R T.A Numerical Pattern Synthesis Algorithm for Arrays[J].IEEE Trans on Antennas and Propagation,1990,38(10)：1666-1676.

[7]王永良,丁前軍,李榮鋒.自適應(yīng)陣列處理[M].北京：清華大學(xué)出版社,2009：220-271.

[8]龔耀寰.自適應(yīng)濾波-時域自適應(yīng)濾波和智能天線(第2版)[M].北京：電子工業(yè)出版社,2003：308-333.