《旋轉試卷講評課》的教學反思

肖瑤

（廣東省廣州市第一一三中學，廣東　廣州　510635）

《旋轉試卷講評課》的教學反思

肖瑤

（廣東省廣州市第一一三中學，廣東廣州510635）

目前許多教師對試卷講評這一特殊課型的重視程度不夠，導致教學效果不佳。本文從《旋轉試卷講評課》的教學目標的分析與確定、教學策略的預設、教學環節和教學效果、成功與不足四個方面進行了反思，希望為如何上好試卷講評課提供借鑒。

旋轉試卷；講評課；教學反思

試卷講評是一個重要而又容易忽視的環節，有針對性地講評試卷，可以查缺補漏，并總結教學的成功與不足之處，以便改進與鞏固提高[1，2]。《新課標》要求把學習過程看作是學生的主體需求的主動體驗和探究過程。以下就是該課的教學反思。

一、教學目標的分析與確定

本節課的重點是找錯因、說考點，培養學生認真審題的習慣；難點是進一步提高學生利用旋轉知識分析了解復雜圖形、動態變化中隱含不變的線段關系。由此確定了該課的教學目標：①知識技能目標：分析學生在做題中的共性問題、錯誤的原因，以錯悟理，強化雙基；針對錯因，加強題型解法引導，滲透數學思想，提高解題能力。②過程與方法考查：設計讓每個學生通過課外獨立思索和小組合作，把握解題思路和方法，解決小組中的部分錯題；課堂展示大部分同學質疑過的錯題，達到查漏補缺的目的。③情感目標：通過講評，培養學生認真審題的習慣，理性看待考試分數，在錯誤中進步，做到不驕不躁，提高學習信心。

二、教學策略的預設

“授人以魚，不如授人以漁”，故本人把重點放在錯題分析和解題思路上，讓學生領悟數學思想和方法在解題中的作用。通過學生自查、析因、糾錯和小組合作交流，培養學生強烈的求對欲，再聽學生代表講評，教師補充、點撥，最后做變式練習，鞏固提高。

三、教學環節和教學效果

1.小結測試，榜樣引入。通過PPT呈現90分以上和進步的同學，營造激勵的學習氛圍，召喚同學們成為優秀生和進步生。

2.小組交流，解決個性錯題。每位同學帶著考卷和自查錯誤反思表，針對尚未解決的問題與小組同學交流，為課堂上解決共性問題做好心理準備。

3.代表講評，變式練習，師生小結。

（1）代表1講評“數軸上點的旋轉”。試卷第10題：數軸上A、B兩點表示的數分別為-1和，點B關于點A的對稱點為C，則點C所表示的數為（ ）。

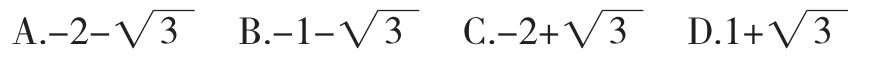
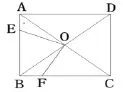
圖1　

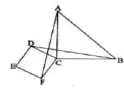
圖2　

（2）代表2講評“旋轉的應用1”：求不規則圖形面積。教師問：沒有平面直角坐標系，如何求不規則四邊形的面積？引入試卷第15題：如圖1，在正方形ABCD中，AC、BD相交于點O，△AOE繞點O逆時針旋轉90°后與△BOF重合，AB=2，則四邊形BEOF的面積是多少？學生邊讀題邊把四邊形BEOF面積涂上陰影，通過旋轉將△BOF搬到△AOE位置，加粗搬動三角形顏色，利用旋轉不變性轉化為求等腰直角△BOF的面積，順利得出答案。本題是針對學生“不會面積轉化”的錯因，點評時強調旋轉前后圖形大小、形狀不變，滲透轉化思想。學生針對試卷第15題做一個相關練習后，教師問：圖形動態旋轉中，如何發現不變規律？

（3）代表3講評“旋轉的應用2”：探索圖形動態中隱含不變的關系。試卷第22題：如圖2，△ABC是等腰直角三角形，其中CA=CB，四邊形CDEF是正方形，連接AF、BD。首先，觀察圖形，猜想AF與BD之間有怎樣的數量關系，并證明你的猜想。若將正方形CDEF繞點C按順時針方向旋轉使正方形CDEF的一邊落在△ABC的內部，請你在原圖下方畫出一個變換后的圖形，并對照已知圖形標記字母。問題①中猜想的結論是否仍成立？若成立，直接寫出結論，不必證明；若不成立，請說明理由。解問題①：學生邊讀題邊把線段的等量關系標在圖形上，要證明線段相等，依次轉為證△ACF≌△BCD和∠ACF=∠DCB，由于∠DCF=∠ACB=90°，所以∠DCF+∠ACD=∠ACB+∠ACD，即∠ACF=∠DCB。解問題②：沒有同學能準確畫出正方形旋轉后的位置，提示正方形的位置變了，但AF=BD關系不變，同樣可以用全等思想證線段相等。本題針對學生“畫圖困難”的錯因，點評時利用幾何畫板動態作圖，告訴學生△BCD可以看成是△ACF旋轉而來，強調旋轉前后圖形形狀、大小不變。學生針對試卷第22題做一個相關練習，教師巡堂，發現大部分學生能利用全等思想。

4.課堂小結，反思歸納。師生一起反思歸納：①圖形的旋轉轉化為__________；②求點的坐標，先定__________，再定________，滲透__________思想；③動態旋轉中，利用________探索不變的面積、線段的相等關系；④通過_____，培養學生認真審題的習慣，貫通學生的知識體系。

5.課后變式作業，鞏固知識。課后布置作業，讓學生獨自審題、思考和探索。

四、成功與不足

1.成功之處。①設計合理，突出重點主線，有針對性。②以學生為主體，體現自主參與性，可激起學生的求知欲望。③利用多媒體和幾何畫板演示，動態直觀，獲得了良好的教學效果，學生在有限的時間內輕松掌握了有關的知識點。

2.不足之處。①心理準備不足：個別學生上臺演示時怯場，影響了效果。②還原考試的情景不足：如設計由不同層次學生分別講述難度不同題目的答題思路，還原考試情境，甚至讓他們提問和質疑，應該更能調動學生的積極性，但事先未考慮到，留下遺憾。

[1]唐先鋒.新課程下初中數學試卷講評課有效性初探[J].教育教學論壇，2010，（9）.

[2]楊艷.初中數學試卷講評課教學策略分析[J].華夏教師，2013，（5）.

G632.0

A

1674-9324（2014）29-0114-02