極區電離層TEC經驗模型的建立及適用性分析

寧新國 安家春 王澤民

（1武漢大學中國南極測繪研究中心，湖北 武漢430079；2長春市測繪院，吉林 長春130021）

0 引言

極區高空大氣是地球大氣層和近地空間最活躍的部分之一，研究極區高空大氣將有助于整體理解太陽風-磁層-電離層-高層大氣-中低層大氣的相互作用［1］。極區電離層作為極區高空大氣的重要組成部分，其監測、建模和預報服務有重要的應用價值。而GPS技術具有成本低、精度高、范圍大等特點，成為研究極區電離層的重要手段。利用GPS觀測數據對電離層TEC（Total Electron Content）進行建模，可以研究電離層的時空變化規律［2-3］，并對GPS信號進行電離層改正［4］。依靠若干GPS觀測站數據可以建立起覆蓋一定區域的電離層模型，與Klobuchar［4］、IRI［5］、Bent［6］等全球電離層模型相比，基于GPS的電離層模型在一定區域的適用性更強。常用的區域電離層經驗模型有多項式模型［7］、廣義三角級數函數模型［8］、低階球諧函數模型［9］、改進的球諧函數模型（又稱偽球諧函數模型）［10］、球冠諧函數模型［11］。為了分析比較以上各種經驗模型在極區的適用性情況，本文利用南極地區2010年40多個測站的GPS數據分別實現了以上五種模型。

1 GPS區域電離層建模方法

1.1 多項式模型

多項式模型是一種結構簡單，顧及到電離層隨緯度、太陽時角變化特征的一種模型，被廣泛地應用于區域電離層模型的建模分析，能夠在一定的時間段以及一定范圍內取得較好的結果。該模型是以穿刺點與區域中心的太陽時角和緯度差作為參量，其表達式如下［7］：

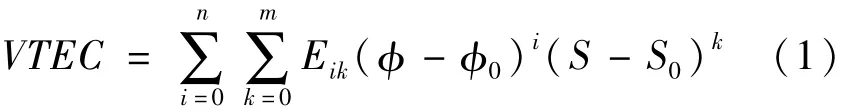
式中Eik即為所要求解的模型系數，φ和S是穿刺點處的地理緯度坐標和太陽時角，φ0和S0是區域中心的地理緯度坐標和太陽時角。……