土石復合介質電阻率特性理論及應用研究

汪 魁，趙明階

(重慶交通大學 水利水運工程教育部重點實驗室,重慶 400074)

0 引 言

近年來，隨著地球物理勘探方法在巖土工程中的不斷普及，電阻率測試技術作為一種最為常用的物探方法，被廣泛應用于各類土石工程的隱患檢測和質量評價中。利用電阻率測試技術對土石工程進行診斷和評價的基礎是巖土介質電阻率特性及理論模型的研究，自從1942年美國測井工程師G.E.Archie[1]利用雙對數坐標研究了飽和砂巖巖樣的電阻率和孔隙度之間的關系以來，國內外已經開展了大量的純土或者巖石介質電阻率特性的研究，其電阻率理論的結構體系相對完善[2-5]，如H.Waxman，等[2]通過試驗研究，提出黏性土顆粒通過表面雙電層的陽離子交換進行導電，將土體的電流傳播假定為是同時通過土顆粒和孔隙水兩條路徑進行的，在此基礎上得到了適用于非飽和黏性土的電阻率模型；國內學者查甫生，等[3-4]在Mitchelll土的三元導電模型的基礎上，推導了非飽和黏性土的電阻率結構模型；劉國華，等[5]通過考慮成巖過程中地層水的變化和陽離子的交換吸附作用, 提出泥質砂巖含水飽和度的雙孔隙導電體積解釋模型。

總之，單純的土體或巖石的電阻率理論已經得到了大量的研究，使得電阻率測試技術在土或巖石的結構性研究中應用均能獲得較滿意的結果[6-9]。然而由于土石復合介質顆粒組成廣泛，粒徑變化較大，其電阻率特性受顆粒的性質和大小、粗顆粒的含量、含水量、壓實干密度等多種因素的影響，相對于純巖石介質或者土體介質，其電阻率理論有著顯著的不同。因此，利用現有的巖石或土體的電阻率理論難以準確地對土石復合介質的物理特征參數進行評價。

鑒于此，筆者在前人研究的純土或者巖石介質的電阻率結構模型的基礎上，基于多相土石復合介質的組成特征，通過建立土石復合介質宏觀導電的物理結構模型，推導土石復合介質的電阻率理論模型，并基于理論模型研究了土石復合介質的電阻率和物理特征參數之間的相關關系。

1 土石復合介質導電特性的物理模型

H.Waxman，等[2]通過試驗研究，提出黏性土顆粒通過表面雙電層的陽離子交換進行導電，將土體的電流傳播假定為是同時通過土顆粒和孔隙水兩條路徑進行的，因此這里假定土石復合介質的電流傳播路徑仍然是包含固體顆粒導電和孔隙水導電兩個方面，但是這里的固體顆粒包括土顆粒和石顆粒兩種成分。因此，需要按照土顆粒和石顆粒組成的不同分別考慮土石串聯模型和土石并聯模型。圖1為土石復合介質導電特性的物理模型。

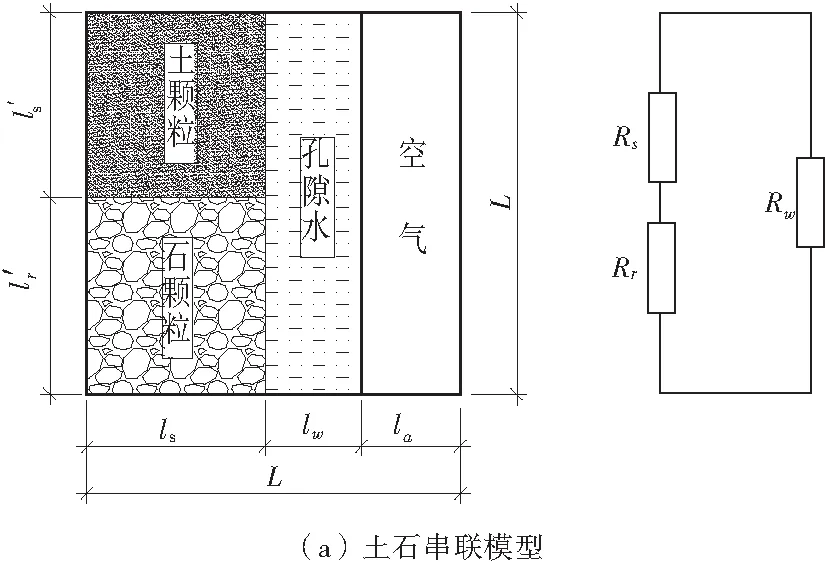
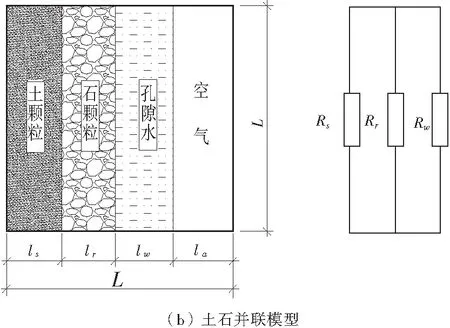
圖1 多相土石復合介質電阻率結構模型Fig.1 Schematic model of the conductivity of multiphase earth-rock mixture

圖1中，假定電流沿著邊長為L的土石混合立方體的豎直方向傳播，假定土石復合介質的總電阻為R，其綜合電阻率大小為ρ，分別根據土顆粒和石顆粒導電的不同組成情況推導土石復合介質的電阻率理論模型。

2 土石復合介質宏觀電阻率理論模型

2.1 土石串聯電阻率結構模型

根據電阻率的定義及歐姆定律由圖1(a)可得關系式(1)～式(5)：

R=ρ

(1)

(2)

(3)

(4)

(5)

式中：Rw，Rs，Rr分別為孔隙水、土顆粒和石顆粒的電阻；ρw，ρs，ρr分別為孔隙水、土顆粒以及石顆粒的電阻率。

利用土石復合介質三相組成的幾何關系推導得到：

ls+lw+la=L=1

(6)

lw+la=nL=n

(7)

(8)

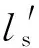
(9)

(10)

式中：n為孔隙率；f為土石體積比；Sr為飽和度。

綜合式(1)～式(10)可得：

(11)

對于多相土石復合介質，其飽和度：

(12)

式中：w為含水量；e為土石復合介質的孔隙比；γde為綜合等效顆粒密度，可以表達為：

(13)

式中：γs為土顆粒密度；γr為石顆粒密度。

孔隙比和孔隙率之間滿足：

(14)

將式(13)、式(14)代人式(12)可得：

(15)

將式(15)代入式(11)可得土石串聯時的電阻率結構模型：

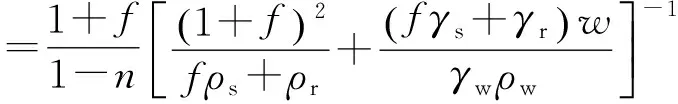
(16)

2.2 土石并聯電阻率結構模型

同理，根據圖1(b)可得土石并聯時的電阻率結構模型為：

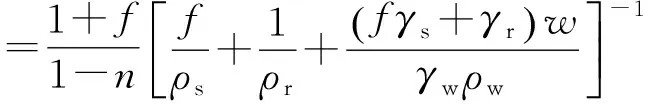
(17)

2.3 土石串聯-并聯混合電阻率結構模型

事實上，土石混合體中土石顆粒的組成應該同時包含串聯部分和并聯部分，若假定土石并聯模型所占比例為ξ，并假定土石串聯和并聯部分符合相同的三相指標關系，則可以建立土石復合介質的串聯-并聯混合導電的電阻率模型為：

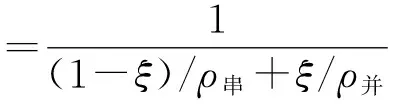
(18)

將式(16)、式(17)代入式(18)可得土石串聯-并聯混合的電阻率結構模型：

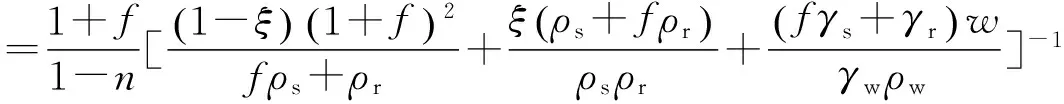
(19)

若取導電結構因子ξ=0.5，則：

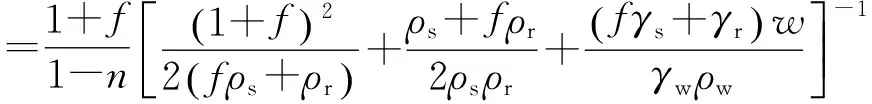
(20)

由式(20)可知，多相土石復合介質電阻率特性主要影響因素包括土、石顆粒的導電性，孔隙水的導電性，土石體積比、孔隙率等。

3 土石復合介質電阻率結構模型的試驗驗證

3.1 試驗設計

配置不同土石比級配良好的土石混合料，通過電動重型擊實儀制作標準的擊實試件(5層56擊，Φ15.2 mm×L11.6 mm)，測試擊實試件的電阻率，分析土石復合介質的電阻率和含水量的相關關系，并與理論計算結果進行對比。

3.2 試驗材料

試驗中的土石混合料為強風化泥巖經風化、剝蝕以及其它物理作用后形成的土石料，首先采用篩分法對天然的土石料的顆粒級配進行分析，如圖2。

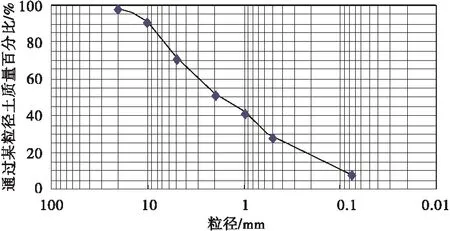
圖2 顆粒粒徑級配Fig.2 Particle size grading

3.3 土石復合介質的界定

土石復合介質是指一種顆粒組成包含土顆粒、石顆粒的土石混合體，其關鍵在于土顆粒和石顆粒粒徑的界定。我國工程中常用固定粒徑5 mm作為粗細顆粒的分界，也就是將<5 mm的顆粒稱為細顆粒、而≥5 mm的顆粒稱為粗顆粒，并且將粗顆粒含量用P5表示。

據M.Edmund[10]、E.S.Linquist[11]和徐文杰，等[12]對土石混合體細觀結構的研究，定義土-石閾值：

dS/RT=(0.05-0.07)Lc

式中：Lc可取測試試樣的直徑。

據此，根據土-石閾值將土石混合體按照顆粒大小劃分成“土”和“石”兩大類：

若按照該標準，以測試試驗的直徑可取土-石閾值為dS/RT=5.8～8.12 mm。

考慮到通過篩分法對土石顆粒進行界定，這里仍然取5 mm作為土石顆粒的界限。

3.4 土石顆粒電阻率的確定

對于土石顆粒的電阻率，H.Waxman，等[2]認為固體顆粒表面吸附了陽離子，而這些被吸附的陽離子可以和孔隙液體中的陽離子進行交換，因此固體顆粒的導電性與可交換陽離子的數量有關，固體顆粒的電導率為：

σs=BQ

(21)

式中：B為雙電層中與土顆粒表面電性相反電荷的電導率,與孔隙水的電阻率密切相關；Q為單位土體孔隙中陽離子交換容量。

實際應用中，要準確的確定巖土體顆粒表面的導電性，需要在合理的假定基礎上通過一定的試驗來獲得。事實上，巖石體的電導率主要取決于孔隙水的含量和導電性，以及固體顆粒表面的導電性等，J.D.Rhoades，等[13]通過室內試驗給出了土體的電導率和孔隙液的電導率以及固體顆粒表面電導率的關系：

σ=aσwθ2+bσwθ+σs

(22)

式中：σ為土體的電導率；σw為孔隙液體的電導率；σs為固體顆粒的電導率；θ為土體的體積含水量。

顯然，巖土體的含水量為0時，其電導率就是固體顆粒的電導率，因此，可通過配制含不同電導性孔隙水(如表1)的土體，測試其電導率(電阻率)，并繪制土體電導率和孔隙水電導率的關系曲線，該曲線在土體電導率軸上的截距就是固體顆粒的電導性。

表1 不同孔隙水的導電性

圖3為土顆粒(粒徑﹤5 mm)、石顆粒(粒徑﹥5 mm)的電導率與孔隙液電導率的關系曲線。

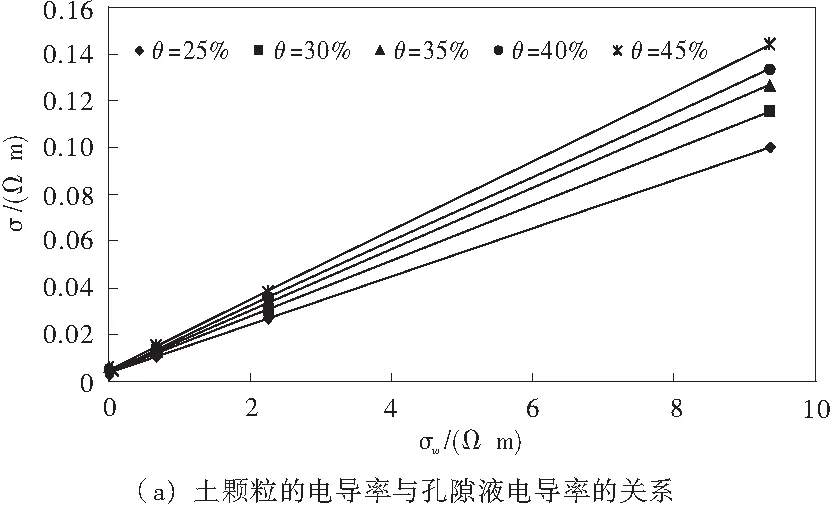
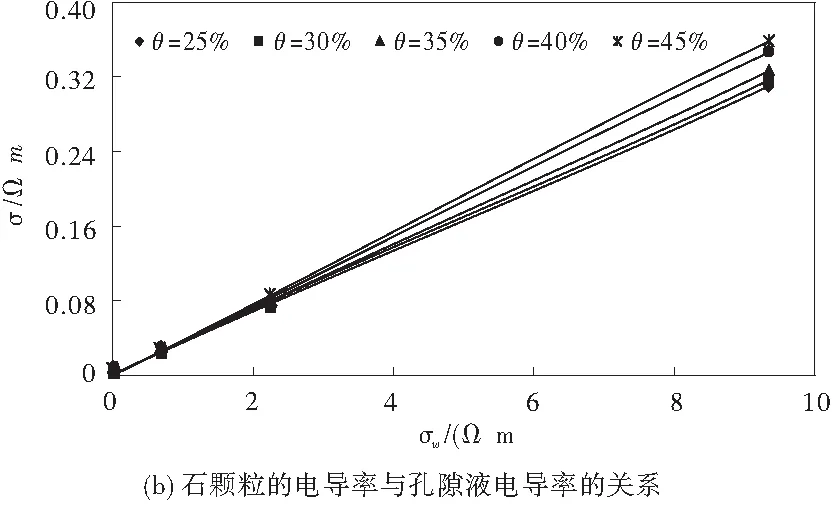
圖3 土石顆粒的電導率與孔隙液電導率的關系Fig.3 Relationship btween electrical conductivity of soil-rock grain and pore water

從圖3(a)可知，到土顆粒的電導率在0.001 7 ～0.003 3 s/m之間變化，取平均值0.002 5 s/m作為土顆粒的電導率，因此，相應土顆粒的電阻率為：

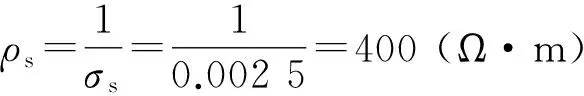
從圖3(b)可知，到石顆粒的電導率在0.001 5～0.002 3 s/m之間變化，取平均值0.001 9 s/m作為石顆粒的電導率，因此，相應石顆粒的電阻率為：

3.5 擊實試件電阻率試驗值和理論值的對比

通過上述試驗方法和數據可得到各個土石比不同含水量下的擊實試件的電阻率實驗值和理論值，如圖4。

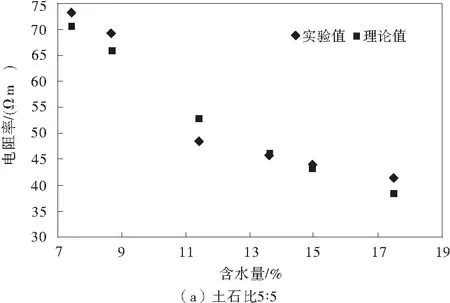
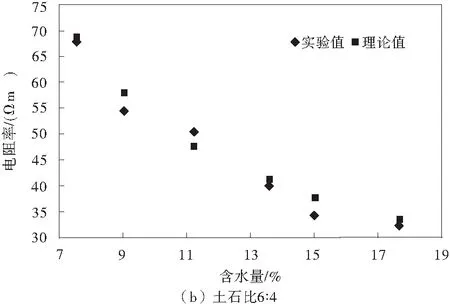
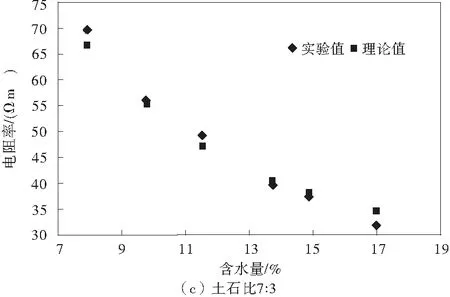
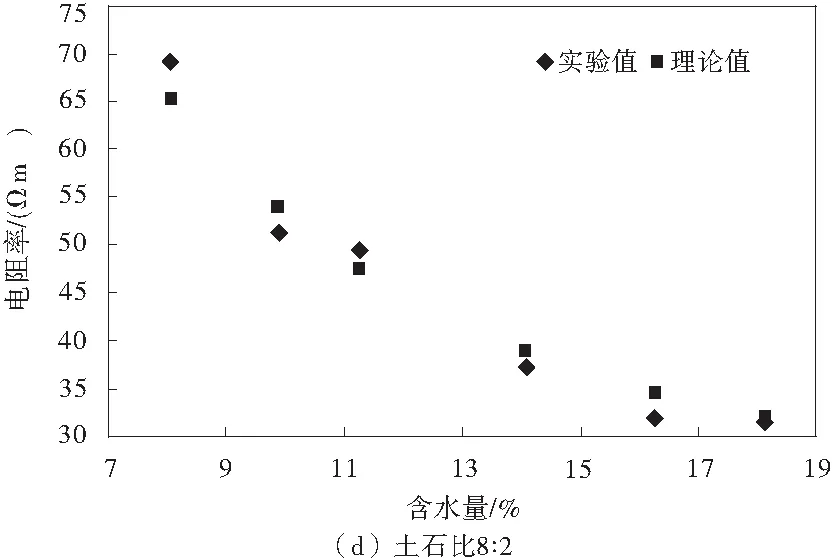
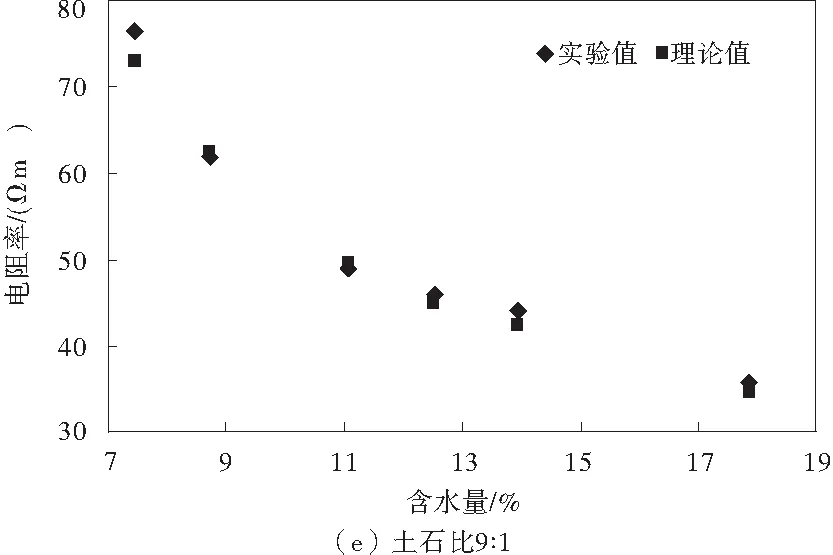
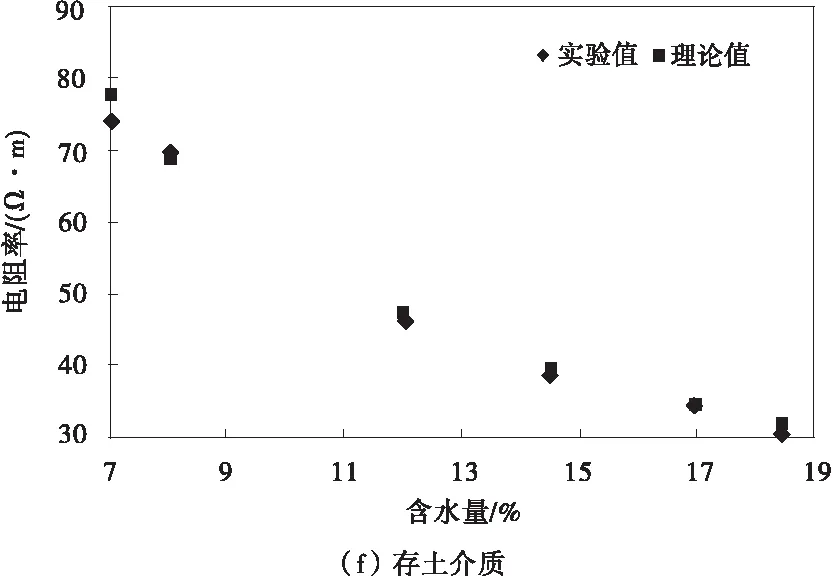
圖4 土石復合介質電阻率理論值與實驗值的對比Fig.4 Comparison btween theoretical and experimental electrical conductivity of earth-rock composite medium

由圖4可知，不同土石比下，各個擊實試件的電阻率理論值和實驗測試值比較接近，而且一般情況下，含水量越大，理論值和實驗值吻合的效果越好，總體來說，式(20)能夠滿足多相土石復合介質電阻率理論測試的精度要求。

4 土石復合介質電阻率結構模型應用

事實上，在巖土工程中，更為關心的是通過電阻率測試能夠反演出的土石物理參數，因此，為了對土石工程的工程特性進行分析，利用文中推導的多相土石復合介質電阻率理論模型對土石工程特征物理參數進行分析。

4.1 含水量的電阻率反演

對于土石填方，如土石地基、土石壩、港區陸域填方等土石工程，每一種填料在相同的壓實條件下，若認為初始孔隙率不變，那么，由多相土石復合介質電阻率理論模型式(20)可得到含水量的表達式：

(23)

同時，有界限含水量：

(24)

若通過電阻率反演出的w>wmax，那么，說明原來的孔隙結構已經發生破壞，土體重新分布。

4.2 孔隙率的電阻率反演

同樣，對于同一填料的土石填方工程，若認為初始含水量是相同的，那么，由多相土石復合介質電阻率理論模型式(20)可得到孔隙率的表達式：

(25)

4.3 干密度的電阻率反演

對于土石填方工程，業界更為關心填方的壓實質量，也就是干密度的大小。對于多相土石復合介質，其干密度的表達式為：

γd=γde(1-n)+nγa

(26)

式中：γa為空氣的密度；n為孔隙率；γd為土石介質的干密度，γde為土石復合介質的等效顆粒密度，按式(27)計算：

(27)

將式(26)表達為：

(28)

由于γa<<γde，因此，式(28)可近似表達成：

(29)

將式(25)、式(27)代入式(29)，可得到干密度的電阻率反演計算公式：

(30)

5 結 論

1)在現有的純土介質電阻率理論基礎上，基于土石復合介質電阻率特性主要影響因素，從固體顆粒成分的組成出發，推導了多相土石復合介質電阻率結構模型，并通過對不同土石比下土石復合介質電阻率的測試驗證了理論模型的可靠性。

2)利用土石復合介質電阻率理論模型，推導了基于電阻率反演土石復合介質特征參數的方法，從而可以針對土石填方工程質量診斷的不同需要(如滲漏診斷、壓實質量評價等)進行定量分析。

3)目前，多相土石復合介質的電阻率理論研究較少，筆者從土石復合介質的等效宏觀特性出發，推導了土石復合介質的電阻率理論模型，建議從土石復合介質的微觀結構出發進一步研究其電阻率特性。

[1] Archie G E.The electric resistivity log as aid in determining for reservoir characteristics [J].Transactions of American Institute of Mining,Metall-Urgical and Petroleum Engineering,1942,14(6):54-61.

[2] Waxman H,Smits L.Electrical conductivity in oil-bearing shaly sand [J].Society of Petroleum Engineers Journal,1968,65(5):1577-1584.

[3] 查甫生,劉松玉,杜延軍.非飽和土電阻率結構模型研究[J].工程勘察,2006(7):1-5.

Zha Fusheng,Liu Songyu,Du Yanjun.Research on electrical resistivity characterization of unsaturated clay [J].Journal of Geotechnical Investigation & Surveying,2006(7):1-5.

[4] 查甫生,劉松玉.非飽和黏性土的電阻率特性及試驗研究[J].巖土力學,2007,28(8):1671-1677.

Zha Fusheng,Liu Songyu.The electrical resistivity characteristics of unsaturated clayey soil [J].Rock and Soil Mechanics,2007,28(8):1671-1677.

[5] 劉國華,王振宇,黃建平.土的電阻率特性及其工程應用研究[J].巖土工程學報,2004,26(1):83-87.

Liu Guohua,Wang Zhengyu,Huang Jianping.Research on electrical resistivity feature of soil and its application [J].Chinese Journal of Geotechnical Engineering,2004,26(1):83-87.

[6] 查甫生,劉松玉,杜延軍,等.黃土濕陷過程中微結構變化規律的電阻率法定量分析[J].巖土力學,2010,31(6):1692-1697.

Zha Fusheng,Liu Songyu,Du Yanjun,et al.Quantitative assessment on change in microstructure of loess during collapsing using electrical resistivity measurement [J].Rock and Soil Mechanics,2010,31(6):1692-1697.

[7] 查甫生,劉松玉,杜延軍.基于電阻率法的膨脹土吸水膨脹過程中結構變化定量研究[J].巖土工程學報,2008,30(12):1832-1839.

Zha Fusheng,Liu Songyu,Du Yanjun,et al.Quantitative research on microstructures of expansive soils during swelling using electrical resistivity measurements [J].Chinese Journal of Geotechnical Engineering,2008,30(12):1832-1839.

[8] 于小軍,劉松玉.電阻率指標在膨脹土結構研究中的應用探討[J].巖土工程學報,2004,26(3):393-396.

Yu Xiaojun,Liu Songyu.Research on application of electrical resistivity indices to the microstructure of expansive soils [J].Chinese Journal of Geotechnical Engineering,2004,26(3):393-396.

[9] 朱家俊,耿斌,耿生臣,等.宏觀導電機理下的泥質砂巖含水飽和度解釋模型[J].石油勘探與開發,2003,30( 4) :75-77.

Zhu Jiajun,Geng Bin,Geng Shengchen,et al.Water saturation explanatory model of argillaceous sandstone under the macroscopically electric conduction mechanism [J].Petroleum Exploration and Development,2003,30(4):75-77.

[10] Medley E.The Engineering Characterization of Melanges and Similar Rock-in-Mixtrix Rocks (Bimrocks) [D].California:University of California-Berkeley,1994.

[11] Lindquist E S.The Strength and Deformation Properties of Mélange [D].California:University of California-Berkeley,1994.

[12] 徐文杰,胡瑞林.土石混合體概念、分類及意義[J].水文地質工程地質,2009,36(4):50-56.

Xu Wenjie,Hu Ruilin.Conception,classification and significations of soil-rock mixture [J].Hydrogeology and Engineering Geology,2009,36(4):50-56.

[13] Rhoades J D,Van Schifgaarde J.An electrical conductivity probe for determining soil salinity [J].Soil Science Society of America Journal,1976,40(5):647-651.