基于類粒子群算法的集裝箱裝載模型優化研究

連志剛，林蔚天，曹 宇，計春雷

(1. 上海電機學院 電子信息學院，上海 201306；2. 上海電機學院 電氣學院，上海 201306)

集裝箱運輸(Container Transport)是指以集裝箱這種大型容器為載體，將貨物集合組裝成集裝單元，以便在現代流通領域內運用大型裝卸機械和大型載運車輛進行裝卸、搬運作業和完成運輸任務，從而更好地實現貨物“門到門”運輸的一種新型、高效率和高效益的運輸方式。學界對集裝箱運輸的相關研究比較豐富，但大部分都集中在泊位指派、船舶的卸載/裝載作業、集卡調度優化、空箱調度、存儲與堆放物流的研究。關于集裝箱內貨物的優化裝載研究還是比較少，并都集中在基于啟發式規則的集裝箱貨物裝載問題[1-4]。基于優化算法和集裝箱貨物裝載的研究較少，并且優化的模型相對簡單[5-6]，離指導實際工作還有很大差距。

通過研究運籌學中集裝箱裝載的經典實例，筆者發現其數學模型有缺欠，按照該模型無法指導集裝箱的貨物裝載，因此，建立了集裝箱裝載模型，并提出求解的方法，利用類粒子群算法對所建模型進行優化。仿真實驗表明，該方法可行有效，對于提高運輸資源利用率和運輸組織效率都具有重要意義。

1 集裝箱裝載實例“數學模型”分析

集裝箱貨物裝載問題常使用的實例見文獻[7]。該實例及數學模型問題詳細分析如下。

某廠擬用集裝箱托運甲乙兩種貨物，每箱的體積、重量、可獲利潤以及托運所受限制如表1，那么兩種貨物各托運多少箱，可使獲得利潤為最大？

表1 承載貨物

依照文獻[7]，該數學模型建立如式(1)。

設甲、乙兩種貨物托運箱數分別為x1，x2，建立的數學規劃如下。

Maxz=20x1+10x2

(1)

模型(1)比較簡單，且有嚴重缺欠。下面用簡單的反例分析上述模型根本不能指導實際，幾乎毫無意義。

反例：某廠擬用集裝箱托運一種貨物，每箱體積、重量、可獲利潤以及托運工具的大小及承重限制如表2，那么該種貨物托運多少箱，可使獲得利潤最大？

表2 承載貨物特征

若參照文獻[7]，設貨物托運箱數為x，則建立的數學模型如下：

Maxz=20x

(2)

若按照模型(2)組織托運，因x=2是該模型(2)的解，即托運貨物2箱，可獲得最大利潤為4 000元。這很顯然存在錯誤，因為托運貨物是箱裝，不能擠壓變形，現實當中是1箱都不能托運，因為貨物超長，根本不能放入。

2 集裝箱貨物裝載數學模型及其優化

2.1 集裝箱貨物裝載數學模型

裝箱問題是指將不同尺寸的物品擺放入有一定容量的容器中, 以獲得某種最佳的效益。裝箱問題是一個具有復雜約束條件的組合優化問題，在理論上屬NP-hard問題。目前所流行的求解集裝箱裝載問題的方法，還沒有一種能有效地求解一切裝箱問題。下面以實例分析，先建立集裝箱貨物裝載問題數學模型。

某廠擬用集裝箱托運貨物，每箱體積、重量、可獲利潤以及托運工具大小及承重限制如表3，那么貨物各托運多少箱，如何裝載可使獲得利潤為最大？

表3 承載貨物清單

設D1，D2，…，Dn貨物托運箱數分別為x1，x2，…，xn，其數學模型如下：

(3)

模型(3)是一個整數規劃，其求解比較復雜，更難的是“裝載的貨物最優擺放后不能超過裝載限制的長、寬、高”。也就是貨物裝載的時候，橫或豎擺放不同直接影響空間的利用效率。不同的擺放方式尋優，其實就是組合優化。下面初步探討模型(3)的求解。

2.2 集裝箱貨物裝載問題求解

集裝箱貨物裝載一般都是從內到外，從下到上，從左到右(從右到左原理相同)依次裝載，至裝滿為止，如圖1。

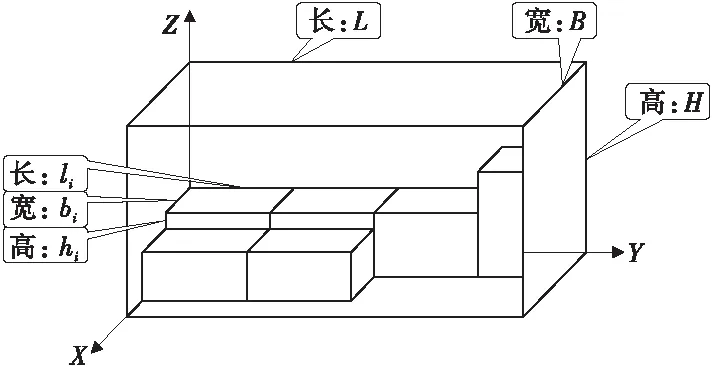
圖1 集裝箱貨物裝載方式Fig.1 Container loading goods mode

針對模型(3)的復雜性，筆者采用迭代進化的方法對其求解。

在數組G1的元素中，可能有m個相同，其表示該裝載方案中有m個相同的貨物；軸對稱相等的邊可以看作是同一條邊；初始解G1表示，以原點為起始點進行裝載，第1個貨物Di的裝載方式為li，bi，hi邊分別與Y，X，Z軸平行；接著裝載貨物Dj，其裝載方式為lj，bj，hj邊分別與Dk貨物的li，bi，hi邊平行；依次類推，直到超出集裝箱的長、寬、高任何一個限制即退出。不妨假設裝載到貨物Dk時，超出了集裝箱長的限制。

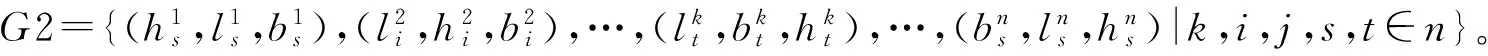
解G2表示以原點為起始點進行裝載，第一個貨物Ds的裝載方式為hs，ls，bs邊分別與Y，X，Z軸平行；接著裝載貨物Di，其裝載方式為li，hi，bi邊分別與Ds貨物的hs，ls，bs邊平行；依次類推，直到超出集裝箱的長、寬、高任何一個限制即退出。不妨假設裝載到貨物Dt時，超出了集裝箱長的限制。重組、迭代時，數組的元素互相“交互”，元素內元素也互相“交換”。

步驟5：當迭代停止條件滿足，輸出數組，即為裝載方案。

下面將用類粒子群優化算法進行詳細模擬，從而徹底解決模型(3)的求解問題。

3 類粒子群優化算法

3.1 類粒子群優化算法編碼

最初提出來的PSO算法是一種基于迭代的優化工具[8-10]。系統初始化為一組隨機解，通過迭代搜尋最優值，并沒有遺傳算法用的交換(Crossover)以及變異(Mutation)，而是粒子在解空間追隨最優的粒子進行搜索。目前已廣泛應用于函數優化，神經網絡訓練，模糊系統控制以及其他遺傳算法的應用領域，但關于OPSO算法應用于NP難的調度問題，報道比較鮮見。

Z.G.Lian，等[11-12]曾用整數編碼方法，借鑒OPSO算法的思想及遺傳算法(Genetic Algorithm, GA)交換(Crossover)操作，采用整數編碼，提出類粒子群算法(Similar Particle Swarm Optimization, SPSO)，并將其應用于有效優化FSSP。劉勇，等[13]利用隨機擴散算法求解二次背包問題。

集裝箱貨物裝載也是一個特殊的背包問題。筆者基于其思想，用類粒子群優化算法解決貨物裝載問題。下面以10箱待裝貨物為例，介紹一些類粒子群算法優化貨物裝載問題的算子操作，其具體編碼如下。

類粒子群算法交換算子操作如圖2。

圖2 類粒子群算法交換操作示意Fig.2 Illustration of the various types of SPSO crossover operators with permutation strings

一段交換(C1)：在父代①和②粒子長度內隨機選擇兩個交換點，將父代①和②交換點內的裝載貨物對應復制到半子代，然后將其互換，如圖2(a)。

兩段交換(C2)：在父代①和②粒子長度內隨機選擇兩對交換點，將父代①和②交換點內的裝載貨物對應復制到半子代，然后將其互換，如圖2(b)。

三段交換(C3)：類似兩段交換，如圖2(b)。

類粒子群算法變異算子操作如圖3。

圖3 類粒子群算法中的變異操作示意Fig.3 Illustration of the shift types of SPSO with permutation strings

一段移動插入(M1)：在父代隨機選擇一段待裝貨物，再移至父代的長度內隨機選擇的插入點后，如圖3(a)。

兩段移動插入(M2)類似于一段移動插入，如圖3(b)。

隨機選擇貨箱翻轉(M3)：在父代粒子長度內隨機選擇幾個待裝貨箱，然后分別隨機選擇翻轉點，將其翻轉點和貨箱長交換，如圖3(c)。

隨機選擇一段貨箱大翻轉(M4)：在父代粒子長度內隨機選擇一段待裝貨箱，將該段內所有貨箱的長、寬、高變為高、長、寬，如圖3(d)。

隨機選擇兩段貨箱大翻轉(M5)類似隨機選擇一段貨箱大翻轉，如圖3(d)。

隨機產生新的待裝貨箱排序(M6)：如產生新種群內新粒子一樣，隨機產生新的貨物裝載序列即可，如圖3(e)。

3.2 類粒子群優化算法遞推方程

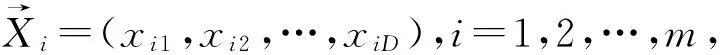
vi(k+1)=pi(k)⊕pg(k)

(4)

(vr1,vr2,…,vrN)(k+1)=M(vr1,vr2,…,vrN)

(5)

xi(k+1)=xi(k)⊕vi(k+1)

(6)

(xr1,xr2,…,xrN)(k+1)=M(xr1,xr2,…,xrN)

(7)

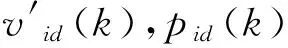
4 類粒子群算法解決貨物裝載仿真

4.1 貨物裝載實例模型

貨物裝載問題為組合爆炸問題，該組合爆炸問題最優解搜索空間非常大，很難搜索到其最優解，有時智能算法搜索到近似解，也很難判斷其是否為最優解。為了檢測筆者提出的類粒子群算法優化貨物裝載問題的可行性，下面給出一個測試實例，進行模擬實驗。為了用數學原理容易找出其最優解，并與筆者提出的智能算法搜索的最優解進行對比，本實例不妨設定的裝載器具、貨物尺寸比較特殊。該實例的集裝箱也可理解為散貨船的船艙，裝載的貨物是不同大小的木箱。該實例及數學模型問題詳細分析如下。

某廠擬用集裝箱托運1種貨物，每箱的長、寬、高、重量、及托運所受限制如表4，那么該貨物最多能托運多少箱？貨物所受體積和重量的最大限制如表4。

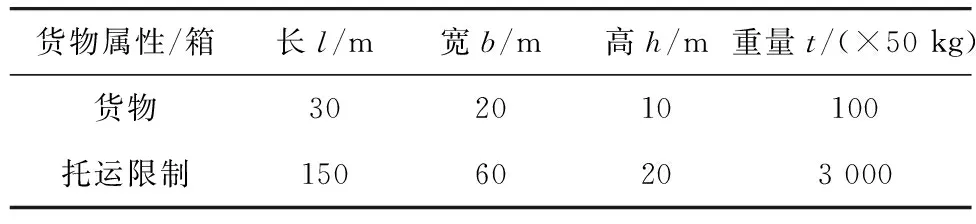
表4 承載貨物實例

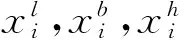
(8)

該問題有許多種裝載方法，為組合爆炸問題。用常用的數學規劃方法解決模型(8)幾乎不可能。筆者采用類粒子群優化算法解決。

4.2 類粒子群算法優化貨物裝載實例模型

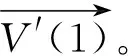
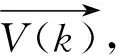
步驟3：輸出pgbest。

用類粒子群優化算法搜索到了模型(8)的最優解，其裝載方法是(30,10,20)針對x,y,z軸的長、寬、高。分別裝長5箱、寬3箱，高2箱，共裝載30箱。筆者用類粒子群算法及遺傳算法對模型(8)進行優化并比較收斂效果，其收斂結果見圖4。

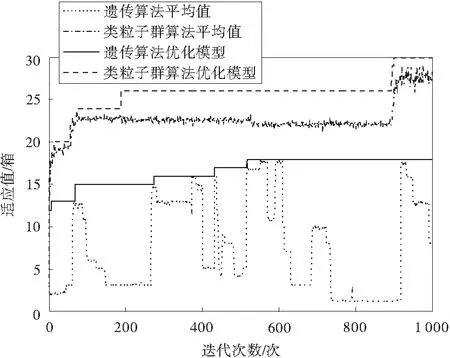
圖4 類粒子群和遺傳算法優化模型(8)的收斂曲線Fig.4 Convergence contrast figure of SPSO and GA algorithmsfor model (8)

從圖4明顯可以看出類粒子群優化貨物裝載模型可行、有效，比GA收斂速度快，并且搜索到得最優解好。

5 結 語

分析發現運籌學中被廣泛使用的一個集裝箱貨物裝載實例數學模型的缺欠，并建立了適合集裝箱運輸實際的集裝箱貨物裝載模型，提出求解所建模型方法，利用類粒子群算法對所建模型進行優化，仿真實驗表明，該方法可行有效，為該類問題的優化尋找了一條新的途徑與方法。

筆者只分析了長方體的同一種貨物在集裝箱中優化裝載的問題。其實當貨物裝載約束條件多時，如不同種類的貨物，大小、重量各異，且貨物托運時某些易損品上面壓力有限制；還有其他球體，錐體及

不規則體等貨物時，其建模及優化更加復雜，是未來研究的一個努力方向。

該文獲得連城物流www.1885656.com;www.11056.net的支持。

[1] George J A,Robinson D F.A heuristic for packing boxes into a container [J].Computers & Operational Research,1980,7(3):147-156.

[2] Pisinger D.Heuristics for the container loading problem [J].European Journal of Operational Research,2002,141(2):382-392.

[3] 劉霞,呂漢興.集裝箱裝載矩形貨物的一種啟發式算法[J].起重運輸機械,2003(1):16-18.

Liu Xia,Lv Hanxing.A heuristic for packing rectangular boxes in a container [J].Hoisting and Conveying Machinery,2003(1):16-18.

[4] 閻威武,邵惠鶴,田雅杰.集裝箱裝載的一種啟發式算法[J].信息與控制,2002,31(4):353-356.

Yan Weiwu,Shao Huihe,Tian Yajie.A heuristic algorithm for three dimension packing problem [J].Information and Control,2002,31(4):353-356.

[5] Gehring H,Bortfeldt A.A genetic algorithm for solving the Container loading problem [J].International Transactions in Operational Research,1997,4(5/6):401-418.

[6] 卜雷,尹傳忠,蒲云.集裝箱運輸多箱三維裝載優化問題的遺傳算法 [J].鐵道學報,2004,26(2):21-25.

Bu Lei,Yin Chuanzhong,Pu Yun.Genetic algorithm for resolution of the three-dimensional multi-bin packing optimization problem in container transportation [J].Journal of the China Railway Society,2004,26(2):21-25.

[7] 錢頌迪.運籌學[M].修訂版.北京:清華大學出版社,2004.

Qian Songdi.Operational Research [M].Revision ed. Beijing :Tsinghua University Press,2004.

[8] Eberhart R,Kennedy J.A new optimizer using particle swarm theory[C]//Proceedings of the 6thInternational Symposium on Micro Machine and Human Science.Nagoya,Japan:IEEE,1995:39-43.

[9] 連志剛,焦斌.一種混合搜索的粒子群算法[J].控制理論與應用,2010,27(10):1404-1410.

Lian Zhigang,Jiao Bin.Particle-swarm optimization algorithm with mixed search [J].Control Theory & Applications,2010,27(10):1404-1410.

[10] 許昆,李智勇.改進的量子粒子群多目標優化算法[J].計算機工程與設計,2009,30 (1):164-167.

Xu Kun,Li Zhiyong.Quantum particle swarm optimization method for multi-objective optimization [J].Computer Engineering and Design,2009,30 (1):164-167.

[11] Lian Zhigang,Gu Xingsheng,Jiao Bin.A similar particle swarm optimization algorithm for permutation flowshop scheduling to minimize makespan [J].Applied Mathematics and Computation,2006,175(1):773-785.

[12] Lian Zhigang,Jiao Bin,Gu Xingsheng.A similar particle swarm optimization algorithm for job-shop scheduling to minimize makespan [J].Applied Mathematics and Computation,2006,183(2):1008-1017.

[13] 劉勇,馬良.隨機擴散算法求解二次背包問題[J].控制理論與應用,2011,28(8):1140-1144.

Liu Yong,Ma Liang.Stochastic diffusion search algorithm for quadratic knapsack problem [J].Control Theory & Application,2011,28(8):1140-1144.