獨立學院大學數學課程成績分析及評價

朱奮秀，汪 韻

（湖北經濟學院 法商學院，湖北 武漢 430205）

獨立學院是我國高等教育發展與改革的重大舉措，對高等教育的普及和發展具有重大的貢獻。但是獨立學院入學的新生與本部大學的學生相比數學基礎存在明顯的差異。而微積分作為經濟管理類學生必修的一門重要的基礎課，擔負著培養學生素養，為后續課程打好基礎并為學生解決實際問題提供必不可少的數學基礎和數學方法，并對專業課的學習有著直接的影響，因此及時對學生的成績進行分析和評價，并對教學工作進行及時的調整就很有必要。

為研究獨立學院的微積分課程學習成績總體情況，以及不同性別，不同的學院，不同教師所帶班級的成績是否有明顯差異，我們不同系里各抽取一部分學生的成績進行分析。本分析研究成果對于學院教學資源的配置，對不同學院，不同性別的學生采用不用的教學方法具有指導意義。

一、原理及分析方法。

SPSS（Statistical Package for the Social Science）社會科學統計軟件是世界著名的統計分析軟件之一，它擁有強有力的數據管理能力，強大統計圖形和制表功能，且擁有專業級的統計分析功能。SPSS還提供一個初級用戶易于學習和掌握的統計分析的用戶界面，簡單的菜單和交互式對話框使得復雜的分析變得簡便，直觀，是我們進行統計分析的理想工具。在本文中，主要使用SPSS軟件的統計分析，獨立樣本T檢驗和單因素方差分析功能處理抽樣所得的數據。

二、數據抽樣

由于我院學習微積分課程的學生較多，如果對所有學生的成績進行普查整理，會加大工作難度，因此采用抽樣的方法進行數據調查。今選取學院2011級第二學期的微積分成績作為本次統計分析的數據，本次抽取四個教學系，七位教師所帶12個班級共569個學生成績。

三、抽樣學生的基本統計分析

基本描述統計量包括平均值，樣本方差，樣本標準差，偏度，峰度，統計結果見表1。

表1 樣本基本統計分析

從統計分析結果來看，學生的平均成績75.95，標準差14.637，樣本方差214.241，偏度-1.109，峰度2.287，可見學生成績分布不是正態分布，呈負偏態分布，也就是成績低于平均值的人數比高于平均值得人數要少。

分析和總結學生成績的呈偏負態分布的原因，我們知道大學期末考試一種合格水平考試，它不同于選撥性考試，它的目的在于考核學生是否達到預定的教學目標和要求，并不要求學生的成績呈現正態分布，反而希望呈現偏負態分布。再者獨立學院的學生數學基礎差，在期末考試之前，任課教師都會學生做大量的模擬練習，認真輔導。教師在命題時，也會考慮到獨立學院的學生的實際情況，題目會出的相對比較簡單，從而導致平時認真學習的學生成績普遍偏高。

四、參數檢驗——檢驗分析學生的性別對學生的成績是否有顯著影響

表2 對男女生兩個獨立樣本參數檢驗

結果表明男女的平均成績分別為70.16和79.14，標準差分別為17.855和11.345，均值誤差為1.256和0.592。在檢驗男女生成績兩總體方程是否相同的檢驗值為33.906，其相伴概率為0，小于顯著性水平0.05，因此拒絕男女生成績方差相等的假設，可以認為男女生成績的方差有顯著性差異，從方差不相等時T檢驗的結果（第二行），T統計量觀測值對應的雙尾概率為0，小于顯著性水平0.05，因此拒絕男女生平均成績相等的假設，也就是說男女生的平均成績存在顯著性差異。上面統計分析結果表明，女生的成績遠高于男生的成績，且比男生的成績穩定。分析造成這種狀況的原因，財經類獨立學院在爭奪優秀生源方面處于弱勢地位，尤其在優秀男生方面的情況更為突出。其次男生在心里發育的成熟度滯后于女生，更容易受外部因素的干擾，容易產生浮躁心態。男生在學習方面缺乏自控能力且不夠努力，而女生在學習方面比男生更加努力和堅持，成績明顯高于男生。

五、單因素方差分析

1.檢驗不同教學系之間學生的成績是否有顯著性差異。

表3 不同系之間學生成績的方差齊性檢驗

方差齊性檢驗的Levene統計量為0.981，所對應的P值為0.401，大于顯著性水平0.05，因此可認為各個系總體方差是相等的。

從方差分析表可以看，方差檢驗的F值為3.921，相伴概率0.009，小于顯著性水平0.05，則拒絕各系學生成績無顯著性差異的假設，也就是說四個教學系中至少有一個教學系的成績與其他教學系的成績有顯著性差異。

表4 不同系之間學生成績的方差分析

從S-N-K法多重比較的結果看到：工商系、國貿系、金融系三個教學系之間，其學生成績無顯著性差異，會計、金融兩個教學系之間，其學生成績無顯著性差異。而會計系學生平均成績與國貿、工商系的學生成績有顯著性差異。

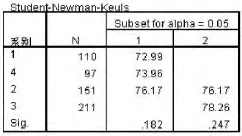
表5 不同系之間學生成績S-N-K多重比較

分析造成系別之間學生成績之間差異的原因，作為財經類獨立學院，學院在會計、金融兩個大方向的實力較強，且會計和金融專業方向的畢業生就業率高，使得大部分成績較好的學生填報會計、金融專業，因此造成在大一的數學課程學習中，這兩個教學系的成績要好于其他系的成績。

2.檢驗教師所帶班級之間學生的成績是否有顯著性差異。

方差齊性檢驗的Levene統計量為0.613，所對應的P值為0.720，大于顯著性水平0.05，因此可認為不同教師所帶班級總體方差是相等的。

表6 不同教師所帶學生成績的方差齊性檢驗

表7 不同教師所帶學生成績的方差分析

從方差分析表可以看，方差檢驗的F值為4.177，相伴概率為0，小于顯著性水平0.05，表示拒絕各個教師所帶班級學生成績無顯著性差異的假設，即七個教師中至少有一個教師所帶班級的成績與其他教師所帶班級的成績有顯著性差異。

表8 不同教師所帶學生成績S-N-K多重比較

通過S-N-K多重比較可得，徐老師所帶班級的平均成績與其他老師所帶班級的平均成績有顯著性差異。通過調查發現徐老師在該學期所帶的這個班是與其他班級合班上課，人數較多，其他老師所帶的班級都是單班上課，人數較少。由此可以看出，大班教學的效果沒有小班教學的效果好。

六、結論

在上述分析過程，我們可以看到，利用SPSS軟件對學生成績的統計分析是非常簡單易行的，通過上面的分析，我們發現女生的成績比男生的成績要好，并且穩定，因此在對待不同性別的學生上，加強對男生學習的管理。不同的教學系之間，會計系的學生成績要顯著的高于其他教學系的成績，說明不同專業的招生的情況對學生成績有顯著的影響。在不同教師之間，由于個別教師大班合班上課，造成大班教學和小班教學之間的成績有顯著差異。因此為了加強課堂的教學管理，提高數學課程的教學質量，培養學生優良的學風，建議數學課程盡量安排小班教學。

[1]王力賓，顧光同.多元統計分析：模型、案例及SPSS應用[M].北京：經濟科學出版社，2010.

[2]陸小華，付申，李媛媛.2003-2004學年高等數學成績分析[J].北京農業職業學院學報，2004，4（18）.

[3]李亞杰.高等院校高等數學課程的成績分析與評價[J].課程教育研究，2012，（2中旬刊）.

[4]劉文艷，龍潤生.SPSS在高等數學成績分析中的應用[J].數量醫藥雜志，2009，3（22）：319-322.