車身小樣本檢測數據多異常值判別方法*
儲國平,韋春洲,鄒景明,尹國麗
(1.上海市數字化汽車車身工程重點實驗室,上海 200240; 2.上汽通用五菱汽車股份有限公司,柳州 545007)
前言
在汽車車身及其分總成和零件的測量數據中,個別測量值在時序上與其他數據有明顯差異,稱之為異常值。異常值產生的原因有兩種,一種由測量粗大誤差引起,如塞尺、面差尺手工測量時的讀數和填寫錯誤,測量儀器的本身缺陷或操作失誤等;另一種由生產過程突變引起,如工人操作失誤,生產環境的突然改變等。異常值若不經恰當處理,會大大影響后續數據處理的精度。而在小樣本狀態下,異常值的檢出更需謹慎,因為數據量較少,一個值對數據整體的影響更大,而且本身樣本量較少,不正確剔除將導致數據量不足,且會丟失重要信息。
常用的異常值判別準則為基于統計的方法[1]有:奈爾檢驗法、拉伊達3σ準則、格拉布斯(Grubbs)準則、狄克遜(Dixon)準則、偏度-峰度檢驗法等。文獻[2]中推導了特殊分布下的異常值檢測方法。文獻[3]中使用Outliar快速算法來檢測離群值,此方法需要大量數據作為計算依據。上述方法都要求數據為正態分布或者分布為已知。但是在車身檢測數據中,由于抽檢頻率低,過程為非平穩,導致在有些時域范圍內數據的分布較為特殊且無法得出分布函數的數學形式[4];有些類型的測量數據受人為調整因素大,例如車門的間隙面差一般需要經過手工調整,或者有些零件經過人為篩選,導致此類數據并不服從正態分布。作為實例,表1列出采用Shapiro-Wilk正態分布檢驗法[5]對車身和發動機蓋零件多個間隙面差測量值的正態性檢驗結果,每次取20個

表1 間隙面差數據正態性檢驗結果
時間點的數據進行檢驗。
由表1可知,有40%左右的間隙面差值不服從正態分布,所以統計法有較大的局限性。
本文中提出了一種基于距離測度的小樣本車身檢測數據異常值的判別方法。每次僅須在時序上提取10個數據進行異常值的判斷,符合小樣本的測量條件,無須預知數據分布情況,可有效處理小樣本(抽檢頻次低,非正態的車身檢測數據)。針對距離測度方法的閾值確定困難問題,提出一種基于排序的閾值確定方法,并通過不同測量位置檢測值之間相關性的比較來區分由生產過程突變造成的異常值和由測量粗大誤差造成的異常值。
1 基于距離測度的異常值檢測
1.1 異常度評價值Fout
在異常值檢測時,首先應確定評價異常度的方法,即一個數據異常程度的度量值Fout。
為判定編號為i的間隙或面差在t時刻的測量值yi,t是否為異常值,在時序上向前取7個點,向后取2個點,總計10個測量值,即[yi,t-7,yi,t-6,yi,t-5,yi,t-4,yi,t-3,yi,t-2,yi,t-1,yi,t,yi,t+1,yi,t+2]
(1)
對上述數據經過標準化處理后得
(2)
計算xi,t與其他測量值的距離:
di,t+k=|xi,t-xi,t+k|(k=-7,-6,…,0,1,2)
(3)
對di,k值進行升序排列,得出新序列Di,k,則xi,t異常程度的度量值為
(4)
稱Fout(i,t)為xi,t的異常度,Fout(i,t)越大則表明異常程度越大。由式(3)和式(4)可知,M決定了多個異常值存在時的檢測能力。例如有xi,t=4.1mm,往前7往后2共取如下10個數據(單位mm):[-1.6,-1.2,-0.7,4.5,0.3,0.9,0.5,4.1,1.3,1.8]
第8個數據為待檢異常值xi,t=4.1mm,但是第4個數據4.5mm也是異常值,即該組數據中共存在兩個異常值,當M=2時,Fout(i,t)=0.149 0;得出的結果是xt的異常度較小,說明此時多個異常值無法檢出;當M=3時,Fout(i,t)=0.224 9;當M=4時,Fout(i,t)=0.260 1,異常度已較高。進一步可得出如下結論。
異常值的個數為N,當M M不應取得過大,否則易受噪聲數據影響,且會造成異常度比較時,不同測量位置檢測值的Fout(i,t)相差很小。 在對車身檢測數據進行處理時,10個時間點的測量數據異常值不應超過兩個,否則視為由生產線故障造成的系統誤差,不屬于異常值范疇,所以選取M=3,可取得較好效果。 計算出某個間隙或面差在t時刻xt的異常度值后,還須判定是否為異常值。 本文中提出一種基于排序的異常值判定方法,通過對多個間隙多個時刻數據的異常度進行排序,挑選出其中異常度較大的值,通過設置閾值Fc,當Fout(i,t)>Fc時判定為異常值,或者選擇排序的前P個作為異常值。本節主要討論Fc的設定方法。 假設在某車型車身(或某分總成、某零件)的歷史數據中間隙檢測點總計有Z個,在時序點上共有T個歷史檢測值,除去最后2個和最早7個,計算每個數據的異常度Fout(i,t)(i=1,2,…,Z;t=8,…,T-2)。由于已經進行過標準化處理,所以相互之間具有可比性,對所有Fout(i,t)按升序排列,總數為Z×(T-9)。以該車型車身兩個月的間隙檢測數據為處理對象,排序后的編號為橫坐標,Fout(i,t)為縱坐標,得出圖1。由圖1可知,在Fc線以上的點為異常度較高的測量數據,軌跡存在明顯的拐點,現在通過設置Fc將這些數據篩選出來。 對上述計算出的Fout(i,t)按異常度畫直方圖得圖2。由圖2可知,在0.2處頻數有明顯下降,經過在某車型車身間隙實測數據中的反復驗證微調,最終取Fc=0.217。 得出Fc后,對于新測量的數據,計算出Fout(i,t)與Fc比較就能分辨出異常值,而無須重新計算Fc。 同一類型的測量數據可共用Fc值,因為同類檢測值的異常值產生原因相同,所以在新車型沒有歷史數據時,可以使用以往車型的同類型數據,但要求這些數據的測量方法相同,以往車型的生產線相似。對于不同類型的測量數據應分別計算其Fc值。 因為測量時極少出現連續出錯的情況,測量粗大誤差產生的異常值主要表現在異常值僅發生在某個間隙或面差處,而附近的間隙面差數據往往正常。 而生產過程突變造成的異常值應歸類為系統誤差,所以在同一個時序點上會有多個相關性較高的間隙面差值同時出現異常值。 據此,區分方法如下。 (1) 對于一組新測量的數據yi,t,間隙面差總數仍為Z個,在同一個時序點t0上從Z個數據中檢出K個異常值。 (2) 兩兩計算K個異常值的相關系數:對于兩個間隙(面差)的異常點,計算方法為先剔除這兩個異常點,分別在兩點各自的時序上向后取4個數據,向前取5個數據組成兩組數據X,Y,每組有9個數據,計算相關系數為 (5) 若前5個數據中存在異常值,則把該異常點所在時序的兩點都剔除,向前取第6個數據遞補。當ρXY≥0.5時,表示兩組數據相關,所以判定這兩個間隙面差間存在相關性,這兩個間隙面差的異常值都由生產過程突變造成。 (3) 若某個異常點在兩兩相關性計算中任一組的ρXY都小于0.5,則說明此異常點由測量原因造成。 表2為上述相同車型車身測試的一批左前照燈與發動機蓋匹配1和2處(圖3)的間隙數據。該車型的間隙異常度閾值已經計算出,適用于該車型車身的Fc=0.217。 表2 左前照燈與發動機蓋間隙的測試數據 mm 兩組間隙數據的第8個點為t時刻待檢測量值,y1,t=8.5mm,進行標準化處理后,間隙1的待檢測量值異常度Fout(1,t)=0.342 8>Fc,判為異常值;y2,t=10.25mm,Fout(2,t)=0.367 4>Fc,也判為異常值。 剔除掉異常點后計算剩余9個數據的相關性ρ12=0.773 5>0.5,所以可以推斷兩間隙的異常值是由生產過程突變,而不是測量粗大誤差造成的。有了這一結果,可快速對異常值來源進行診斷,極大地提高了效率。 表3為上述相同車型車身測試的一批后門與側圍匹配3和4處(圖4)的面差數據。面差的異常度閾值由面差實際數據計算得出Fc1=0.245。本例的車型間隙與面差測量方法不同,所以面差異常度閾值須根據面差測量數據計算,與間隙異常度閾值不能通用。 表3 后門與側圍面差的測試數據 mm 待檢面差測量值為x1,t=4.75mm,計算其異常度Fout(1,t)=0.440 5>Fc1,判為異常值;x2,t=1.5mm,Fout(2,t)=0.088 3 提出一種適用于車身檢測數據特點的異常值判別方法,它對樣本量要求較低,且無須預先假設數據的統計分布特征,從而克服了傳統統計判別方法的缺點。在求得某一類型數據的Fc后,異常值的判別算法簡單有效。以車身前照燈與發動機蓋的實測數據進行了驗證,表明該方法具有較好的實用價值,在某廠車身檢測數據異常值的處理中得到了應用。 參考文獻 [1] 王華.小樣本采樣條件下車身焊裝檢測數據分析與處理研究[D].上海:上海交通大學,2003. [2] 樂立利.觀測數據的異常值統計檢驗方法研究[D].長沙:中南大學,2003. [3] 楊揚,沈紹嶸.白車身尺寸在線檢測的報警算法研究[C].全國質量檢測年會會議論文,2009:37-41. [4] 朱堅民,賓鴻贊.測量數據粗大誤差的非統計判別[J].華中理工大學學報,2000,28(4):17-19. [5] Shapiro S S, Wilkm B. An Analysis of Variance Test for Normality (Complete Samples)[J]. Biometirka,1965,52:591-611.1.2 異常判定閾值
2 異常值產生原因判斷
3 應用實例
3.1 前照燈與發動機蓋間隙異常值判別
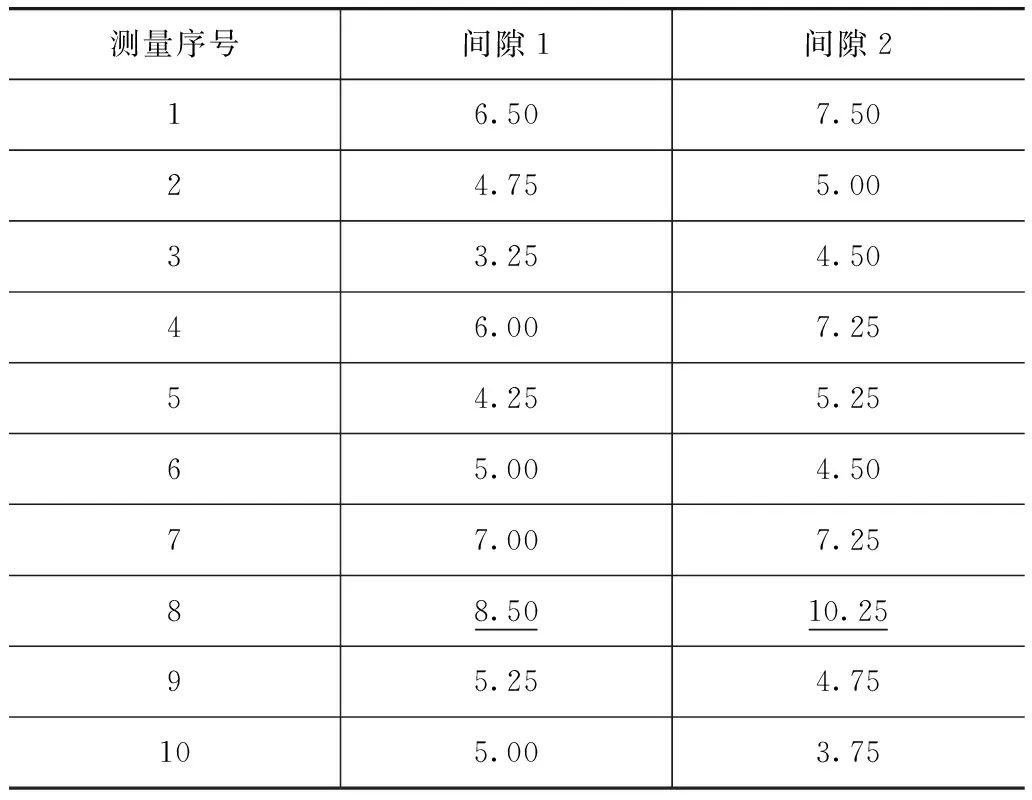
3.2 后門與側圍面差異常值判別
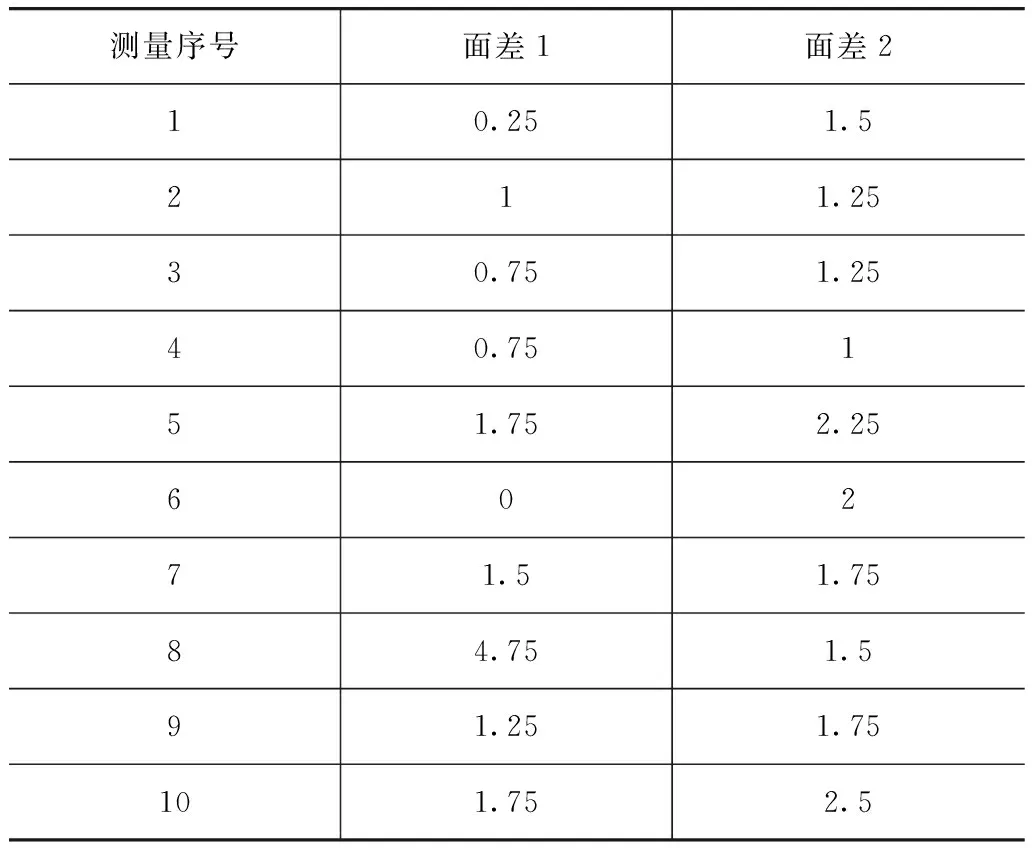
4 結論

