多輪電驅動裝甲車輛車輪防滑控制*

蘇建強，馬曉軍，許世蒙，魏曙光

(1.裝甲兵工程學院控制工程系，北京 100072； 2.66188部隊，張家口 075000； 3.裝甲兵工程學院基礎部，北京 100072)

前言

多輪轂電機驅動裝甲車輛的每個車輪都安裝一個輪轂電機，執行環節只有驅動電機和控制系統，車輛動力學控制的自由度大大增加[1]，對各個車輪的控制提出了更高要求。如車輛在低附著路面加速時，車輪會出現滑轉現象；車輛在過溝過坎時會出現個別車輪懸空，造成車輪傳動系阻力減小，引起車輪“飛車”，故須對車輪實施必要的防滑控制。

汽車電動輪的驅動防滑控制有模糊控制、滑模控制、PID控制和自適應控制等[2-5]。裝甲車輛車輪轉動系統是一個具有參數攝動的大擾動系統，本文中將車輪阻力和車輪參數不確定的部分等效為總擾動，通過擴展狀態觀測器(extend state observe, ESO)估計擾動量，并基于反演(backstepping)逐步遞推思想，將車輪系統簡化為兩個串聯的1階子系統，分別設計滑模控制器。以ESO獲得的擾動估計值代替滑模控制中的切換控制項，抑制傳統滑模控制的“抖振”問題，實現多輪轂電機驅動裝甲車輛車輪的防滑控制。

1 車輪動力學模型

多輪轂電機驅動裝甲車輛裝有8個獨立驅動的輪轂電機，各車輪之間沒有機械連接關系，這就需要對每個車輪都實施防滑控制。車輪在防滑控制時，車輪系統可作為一個獨立的系統。

1.1 車輪轉動模型

車輛在水平路面時的車輪模型為

(1)

式中：m為車輛的總質量；i為電機與車輪之間的傳動比；J為車輪轉動慣量；v為車輛速度；λ為車輪滑移率；r為車輪半徑；ω為車輪角速度；μ(λ)為車輪的附著系數；f為車輪的滾動阻力系數；Te為電機的電磁轉矩；Fz為車輪載荷；ΔFz為車輪動態載荷。

輪轂電機的轉矩瞬態響應性能比車輪的瞬態響應要快幾十倍，將電機的轉矩模型簡化為1階動態系統模型：

(2)

式中：Te_ref為電機參考轉矩；τ為電機轉矩響應時間常數。令x1=ω，x2=Te，u=Te_ref，則可得系統的狀態方程為

(3)

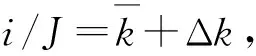
(4)

輪轂電機驅動裝甲車輛的電機轉速很方便測量，轉矩也很容易通過電流計算得到，即狀態變量x1、x2均可實時獲取。

1.2 輪胎模型

通過防滑控制使車輪保持在最佳滑移率附近，使地面提供最大驅動力。根據文獻[6]中縱向Magic輪胎模型：

μ=Dsin{Carctan[Bλ(1-E)+Earctan(Bλ)]}

(5)

式中：μ為縱向附著系數；λ為滑移率；B為剛度系數；C為形狀系數；D為峰值系數；E為曲率系數。圖1為兩種典型路面滑移率與附著系數關系曲線，不同路面的最佳滑移率λd不同，約在10%～25%處。

2 基于ESO的車輪防滑控制器設計

根據上述分析，車輛行駛過程中車輪阻力和垂向載荷變化大，車輪轉動系統是一個具有參數攝動的大擾動系統。滑模控制對參數攝動和外界干擾具有較強的魯棒性，但其切換控制項通過非連續開關切換實現，會引起系統的“抖振”[7]，提出采用ESO估計系統的總擾動，并利用backstepping的逐步遞推思想[8]，將狀態變量x2作為式(4)狀態方程1的虛擬控制量，分別設計兩個狀態方程1階滑模控制器。

2.1 基于ESO的狀態觀測器

擴展狀態觀測器(ESO)將影響被控輸出的擾動擴展成新的狀態變量，用特殊的反饋觀測被擴展的狀態變量(即等效總擾動)。考慮n階系統：

(6)

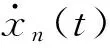
(7)

式中：zi(t)為狀態變量xi(t)的觀測值(i=1,…,n)；zn+1(t)為不確定部分f1(x1,x2,…,xn-1)的觀測值。

由于狀態變量x1、x2均可知，只須對式(4)狀態方程1中F(t)進行觀測。子系統為1階系統，經擴展后為2階系統：

(8)

可得到F(t)的估計值即為z2(t)。

2.2 滑模控制器設計

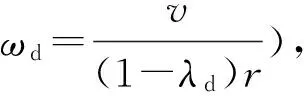
將擾動量觀測值z2(t)代入上式，得到子系統的虛擬控制量：

(9)

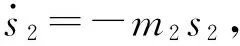
則系統的控制量為

(10)

圖2為系統的控制器結構圖，用ESO對系統中的不確定項F(t)的估計值z2(t)代替滑模控制中的切換項，將狀態變量x2作為系統Ⅰ的虛擬控制量設計了滑模控制器Ⅰ，而后逐步向后遞推，對系統Ⅱ設計了滑模控制器Ⅱ，完成串聯滑模控制器設計。

2.3 控制器穩定性分析

(11)

(12)

3 仿真研究

為驗證控制算法的有效性，對車輛在低附著路面加速和車輪懸空過程進行了仿真。首先通過在給定的固定最佳滑移率下，測試控制的快速性和穩定性；然后在最佳滑移率隨路況變化且輪胎阻力變化較大、車輪轉動慣量攝動的情況下，測試控制器的魯棒性；最后測試車輪懸空時滑移率的控制性能。

仿真前先對車輛的駕駛員加速踏板加以定義：駕駛員需求轉矩Tref=σTmax(n)，σ∈[0,1]為加速踏板的歸一化行程，Tmax(n)為輪轂電機轉矩外特性曲線。輪轂電機的參考轉矩Te_ref=min(Tref,ud)，車輛在高附著路面行駛，車輪實際滑移率很小，防滑控制計算的ud必然大于加速踏板給定的轉矩Tref，此時輪轂電機的參考轉矩由加速踏板給定Te_ref=Tref，防滑不起作用；車輛在低附著路面行駛時，地面不能傳遞駕駛員給定的動力，防滑控制使車輪滑移率控制在最佳范圍，保證車輛以最大動力性能加速。

3.1 最佳滑移率一定的情況下

車輪轉動慣量攝動10%，給定的固定最佳滑移率λ=0.15時，車輛在低附著路面加速仿真如圖3所示。由圖可見，ESO很好地觀測了車輪擾動值F(t)，控制器輸出的輪轂電機轉矩平穩，抑制了滑模控制中的“抖振”問題，滑移率響應快，且滑移率的跟蹤誤差趨近于0，說明前面穩定性分析正確，保證了車輪工作在穩定區，不會在低附著路面出現車輪滑轉現象，車輛以最大驅動力加速。

3.2 最佳滑移率變化的情況下

車輪轉動慣量J攝動10%，地面阻力變化20%，給定最佳滑移率隨路況變化時，車輛在低附著路面加速仿真見圖4。由圖可見，車輪的實際滑移率很好地跟蹤目標滑移率,滑移率的跟蹤誤差趨近于0，抑制了車輛行駛中地面阻力等對車輪的擾動，控制器具有很強的魯棒性。

3.3 車輪懸空的情況下

圖5為車輪懸空時，防滑控制仿真。t=5s時車輪懸空，t=7s時車輪重新落地。防滑控制將車輪在懸空過程中控制車輪在給定車輪最大滑移率，防止車輪“飛車”；在車輪重新接觸地面時，由于地面阻力使車輪的滑移率迅速減小。

通過以上3種情況的仿真，可看出基于ESO的車輪串聯滑模防滑控制器，對系統的大擾動、參數不確定性具有較強魯棒性。滑移率響應快速且無超調，使車輪一直工作在穩定區內，較其他控制方法提高了車輪的穩定裕量和車輛的加速性能；同時也可防止車輪懸空時發生“飛車”現象，提高了車輛行駛的安全性。

4 結論

通過擴展狀態觀測器(ESO)估計車輪轉動時總擾動，利用backstepping的逐步遞推思想，設計了輪轂電機驅動裝甲車輛車輪滑模控制器。以擾動觀測量代替滑模控制器的切換項，抑制了傳統滑模控制的“抖振”問題，且兩個滑模控制器都為1階系統，控制器設計簡單，易于工程實現。

參考文獻

[1] 靳立強,王慶年,岳巍強,等.基于四輪獨立驅動電動汽車的動力學仿真模型[J].系統仿真學報,2005,17(12):3053-3055.

[2] 鄒廣才,羅禹貢,李克強,等.基于模糊DSMC的全輪獨立電驅動車輛滑轉率控制[J].清華大學學報(自然科學版),2008,48(5):860-863.

[3] 趙治國,顧君,余卓平.四輪驅動混合動力轎車驅動防滑控制研究[J].機械工程學報,2011,47(14):83-98.

[4] Lin W S, Chang L H, Yang P C. Adaptive Critic Anti-slip Control of Wheeled Autonomous Robot[J]. IET Control Theory,2007,1(1):51-57.

[5] 周斯加,羅玉濤,黃向東,等.4WD電動車的滑轉率識別及防滑控制[J].華南理工大學學報,2008,36(6):95-100.

[6] 齊志權.汽車ABS/TCS/ASS集成系統中ABS控制技術的研究[D].北京:北京理工大學,2004:21-35.

[7] 左斌,李靜,胡云安.基于反演設計的塊控型極值搜索系統一體化控制方法研究[J].自動化學報,2011,37(9):1115-1129.

[8] Amir Fazeli, Meysar Zeinali, Amir Khajepour. Application of Adaptive Sliding Mode Control for Regenerative Braking Torque Control[J]. IEEE/ASME Transactions on Mechatronics,2012,17(4):745-755.

[9] 韓京清.自抗擾控制技術[M].北京:國防工業出版社,2008:255-263.

[10] 馬曉軍,袁東,李匡成,等.基于擴張狀態觀測器的炮控系統串聯滑模控制[J].光學精密工程,2011,19(10):2409-2418.