電動汽車用感應電機的最小二乘支持向量機逆控制*
陳 龍,孫曉東,江浩斌,徐 興,盤朝奉
(江蘇大學汽車工程研究院,鎮江 212013)
前言
電動汽車由于具有高效率、低污染、低噪聲和電力來源廣等突出優點,被認為是緩解能源危機、改善環境污染的一個重要發展方向,受到了許多國家的高度重視[1-2]。感應電機以其高效方便、體積小、調速范圍廣、調速性能好和控制技術成熟等特點,成為電動汽車主要驅動方案之一。
建立在VC維理論和結構風險最小化原理基礎上的支持向量機(support vector machines, SVM)[3],有效解決了經典機器學習中的局部極小和維數災難等問題,在眾多領域里獲得了成功應用。文獻[4]中提出了一種最小二乘支持向量機(least squares support vector machines, LSSVM)算法,作為標準SVM的一種擴展,在優化指標中采用平方項,用等式約束取代不等式約束,將二次規劃問題轉化為線性方程組的求解問題,因而簡化了計算,使LSSVM在非線性系統的建模與控制中得到較大進展[5-7]。
本文中選擇電動汽車驅動用感應電機作為被控對象,對其數學模型進行可逆性分析。在此基礎上,建立基于LSSVM的感應電機逆模型,并利用改進的粒子群優化(particle swarm optimization, PSO)算法來優化LSSVM的核函數參數和正則化參數。將LSSVM逆模型與原系統相串聯,構成一個復合偽線性系統,再利用已有的線性系統的設計方法來設計反饋控制器進行復合控制。最后在Matlab/Simulink下進行了仿真,結果表明,與傳統的PI控制相比,LSSVM逆控制可使控制系統具有更好的魯棒性和動、靜態性能。
1 感應電機的數學模型與可逆性分析
在d、q兩相旋轉坐標系下,感應電機的狀態方程可用降維的3階非線性模型[8]描述為
(1)
式中:np為極對數;ω1為電氣同步角速度;ωr為轉子電氣角速度;isd、isq分別為d、q軸的定子電流;ψrd、ψrq分別為d、q軸的轉子磁鏈;TL為負載轉矩;J為轉動慣量;Lm為互感;Tr=Lr/Rr為電機轉子時間常數;Lr、Rr分別為轉子電感和電阻。在轉子磁場定向的條件下,有ψr=ψrd,isq=0,這時有
(2)
(3)
代入式(1),系統狀態方程變為
(4)
為判斷其可逆性,式(4)可改寫為
(5)
y=h(x)=[y1,y2]T=[x1,x2]T=[ωr,ψr]T
(6)
其中狀態變量為x=[x1,x2]T=[ωr,ψr]T,控制變量為u=[u1,u2]T=[ω1,isd]T。計算輸出對時間的導數,直至方程中顯含輸入變量,由式(5)得
(7)
(8)
則Jacobin矩陣為
(9)
(10)
由隱函數存在定理可知,式(5)的逆系統為
u=ξ(y,y(1))
(11)
2 最小二乘支持向量機簡介
LSSVM問題可描述如下,對于給定的含有l個樣本的訓練集(x1,y1),…,(xi,yi),…,(xl,yl);其中xi∈Rn為輸入樣本矢量,yi∈R,為輸出樣本矢量i=1,2,…,l;l為樣本個數。則在特征空間中LSSVM模型采用如下函數:
f(x)=wTΦ(x)+b
(12)式中:w∈RH為權向量,b∈R為偏移量,非線性映射函數Φ∶Rn→RH將輸入空間映射至高維Hilbert空間。
LSSVM定義優化問題為
(13)
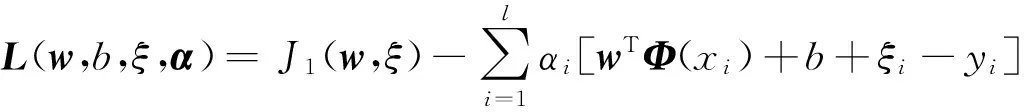
(14)
其中α=(α1,α2,α3,…,αl)T為Lagrange乘子。
根據KKT最優條件,可得
(15)
計算后消去ξi和w,則優化問題可轉化為求解下列線性方程組問題。
(16)
其中:y=[y1,y2,…,yl]T,1l×1=[1,1,…,1]T,I=diag[1,1,…,1],Ω={Ωij}l×l,Ωij=ΦT(xi)·Φ(xj),i=1,2,…,l。
定義核函數K(xi,x)=ΦT(xi)·Φ(x),K(xi,x)為滿足Mercer條件的對稱函數。本文中核函數選取如下徑向基函數:
K(xi,x)=exp(-|xi-x|2/2σ2)
(17)
式中σ為核寬度。則LSSVM回歸的決策函數為
(18)
為了使LSSVM有最好的性能,須對LSSVM的正則化參數γ和核函數參數σ進行優化。
3 用改進的PSO算法優化LSSVM模型參數
3.1 改進的PSO算法
PSO算法是一種基于群體和適配概念群的優化算法[9]。該算法的最優解包含個體最優解和全局最優解兩部分。其中,個體最優解是指每個粒子本身在迭代過程中所找到的最優解;而全局最優解是指當前粒子群中的最優粒子。粒子群中的每個粒子通過追隨個體最優解和全局最優解進行搜索。
假設在D維空間中有m個粒子組成了一個群體,第i個粒子的初始位置和速度可表示為:ui=[ui1,ui2,…,uid]和vi=[vi1,vi2,…,vid],個體最優解和全局最優解分別為:pi=[pi1,pi2,…,pid]和pg=[pg1,pg2,…,pgd],i=1,2,…,m,d=1,2,…,D。粒子群中的所有粒子根據式(19)和式(20)來更新速度和位置。
vi(k+1)=wvi(k)+c1r1(pi(k)-ui(k))+
c2r2(pg(k)-ui(k))
(19)
ui(k+1)=ui(k)+vi(k)
(20)
式中:c1和c2為學習因子;r1和r2為(0,1)間隨機數;w為慣性權重,在進化初期,取w為一個較大的值wmax,以提高算法的全局搜索能力,然后在進化過程中逐步減少,直至最大迭代次數nmax時,w為最小值wmin,w的數學迭代公式為
(21)
式中n為當前迭代次數。
為了解決學習因子和最大速度等參數過大而導致算法的不收斂問題,文獻[10]中引入了收斂因子η,該方法能保證搜索過程收斂,因此本文中采用該改進的PSO算法,則式(19)變為
vi(k+1)=η[wvi(k)+c1r1(pi(k)-ui(k))+
c2r2(pg(k)-ui(k))]
(22)
其中:
(23)
3.2 LSSVM模型評估指標
針對LSSVM需要優化的正則化參數γ和核函數參數σ,建立樣本的均方差eRMSE作為LSSVM的性能評估指標,并將eRMSE作為改進的PSO算法的目標函數:
(24)
當LSSVM的eRMSE較小時,對應的正則化參數γ和核函數參數σ即為優化的參數。
3.3 優化步驟
(1) 獲取訓練樣本和測試樣本,并將樣本進行歸一化處理。
(2) 設置粒子群初始化參數:m=60,d=2,nmax=500,c1=c2=2.05,wmax=0.9,wmin=0.4。
(3) 在定義的D維空間隨機產生m個粒子,設置每個粒子的個體最優解為pi=ui(i=1,2,…,m),隨機產生的初始速度為vi(i=1,2,…,m)。
(4) 評價各個粒子的適應度,將式(24)所表示的LSSVM性能評估指標(即樣本均方差)定義為粒子的適應度函數,即
f(u)=f(γ,σ)=eRMSE
(25)
(5) 對于每個粒子,比較當前的適應度函數f(ui)和歷史最好位置的適應度函數f(pi),若f(ui) (6) 根據式(20)和式(22)更新粒子的位置和速度,產生新的種群,注意速度按如下規則調整: (26) (7) 判斷結束條件。判斷nmax≥500或者f(u)=f(γ,σ)=eRMSE<10-3是否成立,若滿足條件,則尋優結束,否則n=n+1,并跳轉至步驟(4)。 由于LSSVM可逼近任意的一類非線性函數,只要原系統是可逆的,便可用LSSVM來辨識其逆模型。根據LSSVM辨識原理和逆系統控制方法[11],可得到LSSVM逆控制方法完整的實現步驟。 首先,確定激勵信號為常數迭加隨機信號作為系統的速度輸入給定,使原系統充分激勵,以獲得原系統的動靜態特性。LSSVM學習原系統的逆模型時,不但要取得原系統動態時的數據,而且要取得系統靜態時的數據,這樣才能得到完整的逆模型。因此輸入給定的選擇應覆蓋感應電機的整個工作區域,保證系統獲得足夠豐富的訓練數據。此外采樣的準確度直接影響系統辨識的結果,從而影響控制的效果,在測量過程中,由于現場存在各種隨機的噪聲干擾,以及測量器件本身的誤差,測量值與真實值存在一定誤差,因此對采樣數據進行了二階濾波。應特別指出的是,須對速度給定信號的變化周期進行適當的選擇,以避免出現實際系統來不及跟蹤給定信號,而始終處于動態過程的情況。各種給定信號的變化周期取10s,保證了采樣的響應數據包含了系統的動靜態信息,速度的采樣周期為0.1s,得到約4 000個采樣數據。 其次,采用高階數值微分方法離線求出速度輸出響應的一階導數,然后等間隔地抽取出d=1 000組構成訓練樣本集{xi,ui}(i=1,2,…,d),其中,x=[y(1),y]=[ωr(1),ωr]為LSSVM學習的輸入數據,u=ω1為LSSVM學習逆系統的期望輸出。 再次,由獲取的訓練樣本,根據3.3節所述方法優化LSSVM的正歸化參數γ和核寬度σ,優化后的參數為γ=950,σ=2.6,并且LSSVM的性能評估指標eRMSE為3.421×10-3。通過LSSVM的學習,獲得相應的輸入向量系數αi和閾值b,根據當前的輸入x,可以辨識出逆模型的輸出為 (27) 將求得的基于LSSVM的逆系統串聯在原系統之前,就構成了一階偽線性復合系統,該復合系統實現了原系統的輸入輸出線性化,如圖1所示。 (28) 仿真研究中的感應電機參數為:額定功率Pe=5kW,定子電阻Rs=5.35Ω,轉子電阻Rr=4.85Ω,定子電感Ls=0.41H,轉子電感Lr=0.46H,互感Lm=0.47H,轉動慣量J=0.018kg·m2,額定負載為16N·m,額定角速度ωN=160rad/s。 從樣本數據另外集中選取1 000組數據作為測試數據,用作對所建系統的逆模型的預測性能分析。為了衡量預測模型的性能,定義以下幾個性能指標: 預測均方根誤差(εRMSE) (29) 最大絕對誤差(εMAXE) (30) 為了比較所建逆模型的有效性,分別采用BP神經網絡、經典SVM和經過改進PSO算法優化的LSSVM建立電動汽車用感應電機系統的逆模型,對所選的1 000組測試數據的預測均方根誤差(εRMSE)、最大絕對誤差(εMAXE)和CPU運行時間進行了對比,結果如表1所示。 表1 所建逆模型的預測效果比較 BP神經網絡模型采用2-7-1的3層網絡結構,隱含層和輸出層神經元均采用如下Tansig函數: (31) 經典SVM的核函數采用徑向基函數。 由表1可見,用改進PSO算法優化的LSSVM方法建立的逆模型,其預測精度優于BP神經網絡和經典SVM所建的逆模型,不僅有效避免了BP神經網絡建模過程中存在的過學習、局部極小與維數災難等問題,而且很好地解決了經典SVM對于大容量樣本的計算復雜和計算速度緩慢等問題。 為驗證本文所提控制策略的有效性,與傳統單純PI控制方法進行了比較。圖3為系統跟蹤方波給定信號的速度跟蹤響應曲線;圖4為系統跟蹤三角波給定信號的速度響應曲線。從圖3和圖4中可看出,采用本文中的控制策略時,系統的動靜態特性好,跟蹤效果理想,跟蹤精度高。 為進一步驗證本文中所提控制策略的抗干擾能力,在100s時對系統突然變載,負載由12N·m突變到16N·m。傳統PI控制和LSSVM逆控制下系統的轉矩和角速度響應曲線見圖5和圖6。由圖5和圖6可知,采用傳統PI控制方法,當負載轉矩變化時,電磁轉矩雖能在較短時間達到汽車行駛時所要求的穩定狀態,但是轉矩波動較大,且負載突變對角速度有明顯的下降;而采用LSSVM逆控制方法時,轉矩波動較小,特別是負載突變對角速度幾乎沒有影響,說明LSSVM逆控制具有更好的魯棒性。 針對傳統逆控制方法中逆模型難以建立的問題,提出了使用LSSVM求取逆模型的方法,并采用改進的PSO算法優化LSSVM的性能參數,對電動汽車驅動用感應電機這一非線性、快速多變的復雜對象,運用LSSVM逆方法進行了控制研究,并取得了滿意的控制效果。仿真結果表明,系統具有優良的動、靜態控制性能,并具有良好的魯棒性。 參考文獻 [1]ChanCC.TheStateoftheArtofElectric,Hybrid,andFuelCellVehicles[J].ProceedingsoftheIEEE,2007,95(4):704-718. [2] 莊幸,姜克雋.我國純電動汽車發展路線圖的研究[J].汽車工程,2012,34(2):91-97. [3]VapnikV.StatisticalLearningTheory[M].NewYork:WileySpringer,1998. [4]SuykensJAK,VandewalleJ.LeastSquaresSupportVectorMachineClassifiers[J].NeuralProcessingLetter,1999,9(3):293-300. [5]MiranianA,AbdollahzadeM.DevelopingaLocalLeast-squaresSupportVectorMachines-basedNeuro-fuzzyModelforNonlinearandChaoticTimeSeriesPrediction[J].IEEETransactionsonNeuralNetworksandLearningSystems,2013,24(2):207-218. [6]HacibT,LeBihanY,SmailMK,etal.MicrowaveCharacterizationUsingRidgePolynomialNeuralNetworksandLeast-SquareSupportVectorMachines[J].IEEETransactionsonMagnetics,2011,47(5):990-993. [7]YuLA,ChenHH,WangSY,etal.EvolvingLeastSquaresSupportVectorMachinesforStockMarketTrendMining[J].IEEETransactionsonEvolutionaryComputation,2009,13(1):87-102. [8] 陳伯時.電力拖動自動控制系統[M].北京:機械工業出版社,2006. [9]KennedyJ,EberhartRC.ParticleSwarmOptimization[C].ProceedingsofInternationalConferenceonNeuralNetworks.NewYork:IEEE,1995:1942-1948. [10]ClercM.TheSwarmandtheQueen:TowardsDeterministicandAdaptiveParticleSwarmOptimization[C].ProceedingsoftheCongressonEvolutionaryComputation,Washington,USA,1999:1951-1957. [11] 李春文,馮元琨.多變量非線性控制的逆系統方法[M].北京:清華大學出版社,1991.4 LSSVM逆控制方法的實現
5 仿真研究
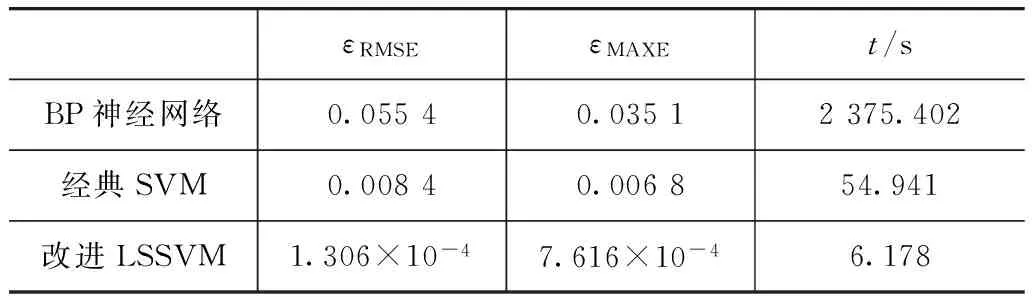
5.1 所建逆模型的預測效果比較
5.2 LSSVM逆控制結果分析
6 結論

