綜合時間序列與高程的天頂對流層延遲模型研究

周淼 ，劉立龍，張騰旭，張朋飛，黃良珂

(1.桂林理工大學測繪地理信息學院，廣西桂林 541004;2.廣西空間信息與測繪重點實驗室，廣西桂林 541004)

1 引言

隨著衛星定位技術的迅猛發展，在實際應用中對定位精度的要求越來越高，而對流層延遲是定位精度影響的。削弱對流層影響的方法主要有參數估計法、模型改正法等［1］。其中在模型改正法中，傳統的對流層改正模型 Hopfield［2］及 Saanstamonien［3］能對流層延遲誤差，但在區域對流層延遲改正中精度不能滿足需求。為此許多國內外學者提出建立區域對流層模型來消弱對流層延遲的影響，其可行性和有效性都得到了廣泛證明［4～6］。文獻［1］、［4］分別利用廣西地區區域CORS網實測數據和香港CORS網數據建立了廣西地區及香港地區的精密天頂對流層延遲新模型，其精度與一般模型精度相比更優。

本文采用加州福利亞地區26個IGS站近4年(2008年～2011年)的天頂對流層延遲數據，通過對傅里葉五階函數所確定的對流層年周期變化函數和指數函數的加權組合，得到了加州地區區域天頂對流層延遲模型。

2 模型的建立

2.1 數據分析

本文采用加州地區26個永久跟蹤站(IGS)4年天頂對流層延遲數據，其采樣間隔為 30 s，采用 Bernese GPS Software Version 5.0解算，其精度優于 4 mm。其經度分布為240.48°～243.61°，緯度范圍為33.25°～33.93°，高程范圍為 －27.56 m ～842.55 m。

為了研究加州地區的ZTD與經緯度及高程之間的關系，分析了4年平均ZTD與經緯度高程三者之間的相關系數，其分別為 －0.377 1、－0.295 8、－0.998 5。從相關系數可以看出，在研究區域的ZTD與緯度存在中等相關，在研究區域的ZTD與經度存在弱相關，而與高程存在強相關。故在接下來的研究中剔除不顯著的影響因素，只保留影響因素較大的高程因素。

為研究ZTD與時間序列(即年積日)的關系，選取了高程間隔大致相同的 sio3、csn1、rock、gold、chil等 5個站的4年平均ZTD和研究區域所有站點total 4年的平均ZTD來進行分析。從圖1中可知，各站ZTD隨年積日的改變而呈曲線變化，且變化趨勢相同，故可以利用相關函數擬合，如傅里葉函數、高斯函數或者多項式函數等。

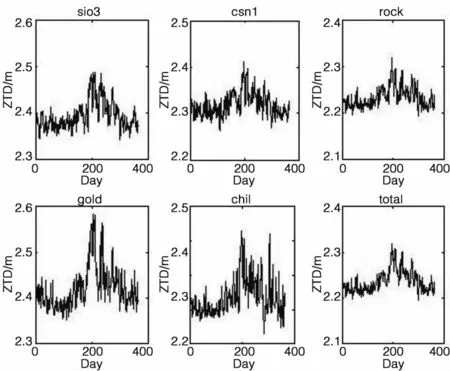
圖1 研究區域ZTD與年積日的關系

2.2 與高程相關函數模型的建立

ZTD與高程的關系成負指數相關或線性相關，在結合研究區域實際情況下比較得出兩者并沒有較大差異，指數擬合稍好于線性擬合［1］。由指數函數擬合對流層得到方程為:ZTD(H)=a·exp(－b·H) (1)經擬合后可解出方程參數，其中a=2.222，b=0.07222。

2.3 與時間序列相關函數模型的建立

將加州地區IGS站點4年日平均ZTD相加取平均值，再分別利用傅里葉函數(F表示，F5表示傅里葉五階函數，其他類同)、高斯函數(G表示)、多項式函數(P表示)擬合，其RMS如表1所示，擬合圖如圖2所示:

數據處理前后中誤差 表1

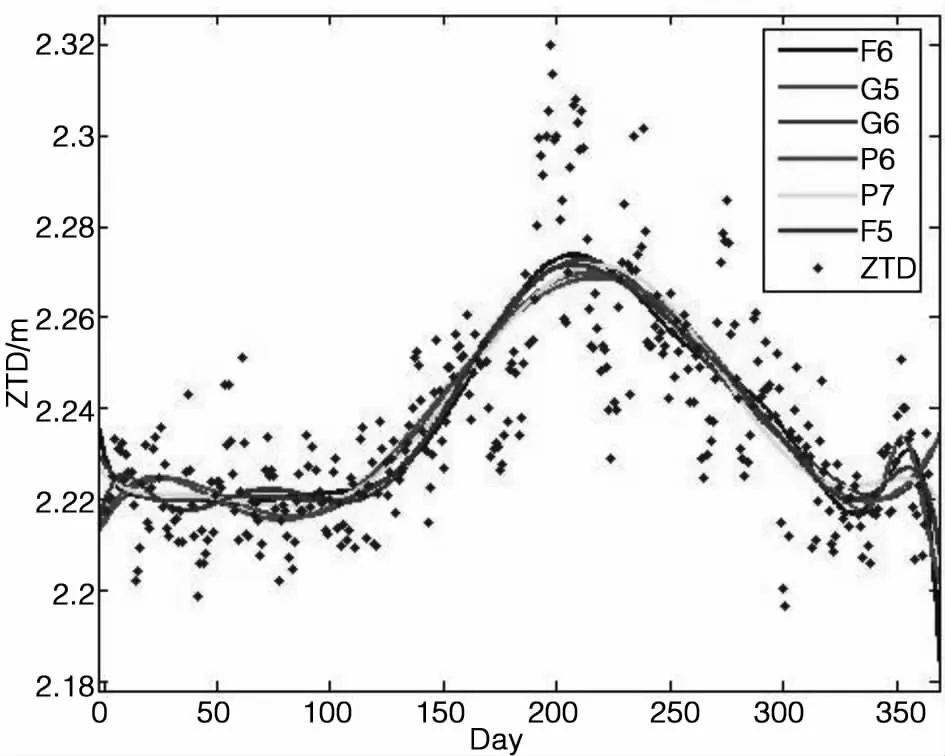
圖2 平滑前各曲線擬合模型擬合圖

由表1可知，在選擇初始函數時，各模型的中誤差比較接近，改變模型的階數并不能有效提高模型精度。但在高階函數中，階數過高使得兩端噪聲過高，階數過低又不能很好反映數據變化規律，從圖2上可以看出傅里葉模型、高斯模型和高階多項式模型中，噪聲在數據的開端及末尾波動比較劇烈。在本文中，傅里葉五階函數在噪聲方面比較小，在數據兩端波動較平緩，綜上，選擇傅里葉五階函數作為時間序列的擬合模型。

2.4 綜合時間序列與高程的天頂對流層延遲模型的建立

由以上綜合分析知道，與加州地區天頂對流層延遲相關的因素主要為高程及時間序列，因此可以建立起加州地區與高程及時間序列的對流層延遲模型。模型為:

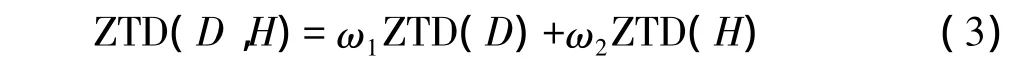
其中，ZTD(D，H)為本文建立的對流層延遲模型，D為年積日，H為高程，ZTD(D)傅里葉五階擬合函數，ZTD(H)為高程指數擬合函數。

按照經驗定權規則，其定權規則為:

式中，△i(i=1，2，…n)為各影響因素的最大值與最小值之差。研究區域中，最低 lbch站的高程為－27.56 m，年均ZTD為 2.380 m，最高monp站的高程為 1 842.55 m，年均 ZTD為 1.900 m，兩站之間的ZTD相差為 0.356 m。在各站365天平均取得的ZTD中最大值與最小值之差為 0.123 m，由此可得研究區域的對流層延遲模型為:

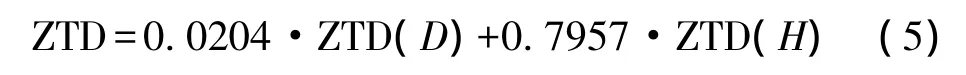
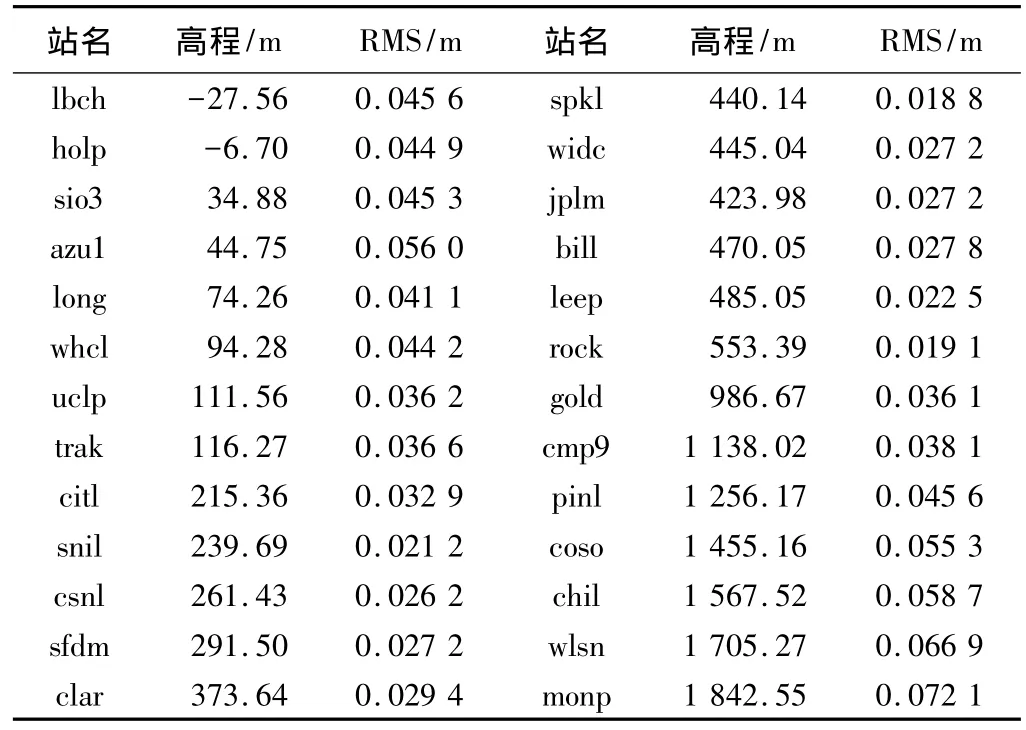
各站經擬合后中誤差 表2

按式(5)來計算加利福尼亞地區的ZTD得出的值見表2，由表2可以看出，中誤差變動幅度較大，成兩頭大中間小的趨勢。具體表現為在站點高程低于100 m時，其中誤差都大于 4 cm，其中最大的為azu1站，為 5.6 cm;當高程在 100 m～1 000 m左右時，中誤差總體變化比較平穩，且精度比較高;在高程大于1 000 m左右時，其誤差波動較大，其中最大誤差出現在高程最大的monp站，其中誤差為 7.21 cm。顯然在高程在 100 m以下、1 000 m以上的區域，其擬合精度有改進空間。經分析，方程(1)的用傅里葉五階函數擬合加州地區的ZTD，可以反映出ZTD隨時間變化的規律，但在數據擬合用的這一區域所有IGS站4年平均對流層延遲，在高程較高和較低的地區沒有很好地反映這類地區的ZTD，故可以對高程分段擬合，接下來對加州地區對流層模型加以改正。

改正方法:抽取高程小于 100 m，高程在 100 m～1 000 m之間和高程大于 1 000 m的3個層次分別進行以上步驟進行擬合。其擬合精度如表3所示。

各站改正后中誤差 表3

從表3中可以看出，在進行高程分區后，各站點的精度有明顯提高，尤其是在高程的兩端，其效果更加明顯。

3 模型的預報

為了驗證模型的實用性，本文用IGS站各站點的2012年的數據進行驗證性試驗。由于2012年中許多站數據的缺失和不完整性，剔除不滿300天數據的站點。其可用站點的天頂對流層延遲中誤差如表4所示。

模型預報2012年ZTD中誤差 表4

從表中可以看出，在預報2012對流層延遲中，模型的精度在厘米級，其中精度最低的點是azu1站，為5.86 cm;精度最高的點是cmp9站，為 3.09 cm。平均精度為 4.31 cm，因此該模型精度能滿足GNSS米級定位精度對流層延遲改正需要。

4 結論

本文建立的天頂對流層模型較為簡單，不需要實測氣象參數，且需要的參數較少。由于是建立在該地區的模型，具有地域特性，能較好反映當地對流層變化規律。在研究區域，對流層延遲與經緯度沒有顯著關系，與高程存在較強的相關性。通過擬合比較分析，發現五階傅里葉函數擬合模型及高程指數擬合模型能較好反映該地區對流層變化。新模型在預報對流層延遲時，其平均精度可達到 4.31 cm，該模型精度可滿足GNSS米級定位精度對流層延遲改正需要。本文建立的模型是以每日的天頂對流層數據來建模，因此在小尺度時間上具有一定的局限性。

［1］ 劉立龍，黃良柯，姚朝龍等．基于區域CORS網天頂天頂對流層延遲4D建模研究［J］．大地測量與地球動力學，2012，32(3):45 ～46．

［2］Hopfield H S．Journal of Geophysical Research［J］．1969，74:4487．

［3］Saastamonien J．Contributions to the Theory of Atmospheric Refraction［J］．bulletin Geodesique，1972，105(1):279 ～298．

［4］李薇，袁運斌，歐吉坤等．全球對流層天頂延遲模型IGGtrop的建立與分析［J］．科學通報，2012，57(15):1317～1318．

［5］戴吾蛟，陳招華，匡翠林等．區域精密天頂對流層延遲建模［J］．武漢大學學報·信息科學版，2011，36(4):392 ～393．

［6］盧獻健，晏紅波，任超．常用天頂對流層區域擬合模型的比較分析［J］．全球定位系統，2010，26～26．

［7］曲偉菁，朱文耀，宋淑麗等．三種天頂對流層延遲改正模型精度評估［J］．天文學報，2008，49(1):113～114．