圓變方孔型的系數設計法

曹國富

（佛山市萬乘實業有限公司，廣東 佛山 528315）

0 前 言

焊管先成圓后成方的工藝在中小型焊管生產線上應用十分廣泛，設計方法也多種多樣，但都存在兩個問題：①需要人為設定一個變形參數，以推動整個設計得以進行。這樣就因個人知識多寡、經驗豐歉等因素產生一定的設計風險；②大多計算較為繁雜，計算量大，設計效率低。

圓變方孔型的系數設計法既不需要人為設定變形參數，又能簡化設計程序、減少計算量、提高設計效率，并且對本次設計效果可預知。這是因為圓變方孔型的系數設計法有其獨特設計方法和設計思路。

1 圓變方孔型系數設計法的思路

圓變方設計的初始圓及變形花如圖1所示。可看出，在按公稱尺寸設計孔型時，初始圓上(a在數值上等于方管邊長a（以下均用a表示），則先成圓之圓直徑D與方管邊長a存在（1）式所示的函數關系

同時，圓變方之初始弓形高h與方管邊長a也存在（2）式所示的函數關系

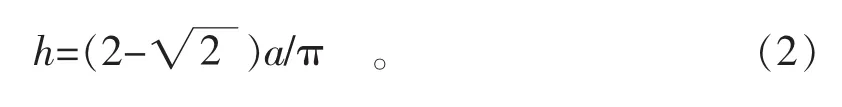
圖1 圓變方設計的初始圓及變形花

雖然（1）式和（2）式對圖1而言表達的內容不同，但是都是以 “系數×方管邊長”的形式表現方管邊長與圓的關系。這意味著有可能通過一定的數學變換，將各道孔型各部位曲線的函數表達式也變換成 “系數與方管邊長”相乘的形式，并且，由（1）式和（2）式所決定的各道次設計系數應該對所有圓變方孔型都適用。或者說，在總變形道數一定的情況下，所有圓變方孔型第道次的設計系數都相同。倘若能實現這一構想，那設計圓變方孔型就簡單方便快捷多了。

2 圓變方孔型的系數設計法

2.1 系數設計法的內涵

根據設計思路，所謂圓變方孔型的系數設計法是指將圓變方孔型各道次、各部位曲線的函數表達式都以一個對應固定的系數μi（λi）或一個關于μi（λi）的表達式與方管邊長a相運算的形式來表示，即

式中：ai（a）—圓變方孔型第i道次內接正方形邊長的函數；

Ri（a）—圓變方孔型第i道次變形半徑的函數；

λi—關于函數ai的各道次孔型設計系數；

μi—關于函數Ri的各道次孔型設計系數；

i—變形道次；

N—總變形道次數。

式（3）這組函數關系一但確定之后，就對所有圓變方孔型都適用。該式兩個方面的含義：

（1）在變形總道數已定和按公稱尺寸設計原則設計孔型的前提下，所有圓變方孔型的設計系數只有 N 對，即 μi=μ1，μ2…μN和 λi=λ1，λ2…λN，且每道孔型不論方管邊長如何變化，也不管是箱式孔型還是斜出孔型，都只有唯一一對設計系數與之對應。

（2）在每一個圓變方孔型表達式中，只涉及兩個參數，一個是被固化了的設計系數 （μi或λi），一個是方管邊長a。由此可見，在系數設計法中，真正的變量是方管邊長a。設計時，只需將自變量a帶入進行運算即可獲得圓變方孔型參數。

當然，這些是以一定設計原則為前提的。

2.2 系數設計法的設計原則

2.2.1 以弓形高為變形量的原則

在圓變方過程中，實質上是弓形高從初始值變為0的過程。之所以選擇弓形高為變形量，是因為采用平均遞減弓形高來變形，管坯變形比較平穩，軋輥孔型面受力也比較平均。由（2）式得弓形高的道次平均遞減變形量

繼而，弓形高的道次變形量

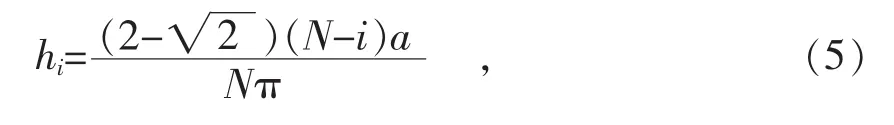
式中，當變形道次i=N時，hi=0，完成圓變方變形。

2.2.2 以公稱尺寸代替孔型弧長的原則

在采用圓變方工藝設計方孔型時，目前是借助道次壓下系數來解決管坯變形中發生的周向收縮，并據此作為設計各道各段孔型弧長的依據。可是，由道次壓下系數所決定的量平均到各段弧長上一般只有幾十微米至一百多微米（中小直徑圓管范圍），而在圓變方過程中影響實際變形效果的因素較多，如材料、工藝、操作、公差等。只要這些因素中任意一個沒有達到理論設計要求，那么，采用道次壓下系數設計孔型曲線長度就形同虛設和微不足道了。因此，直接用成品管公稱尺寸作為設計孔型曲線弧長的依據，讓每段孔型對應的曲線長都與公稱尺寸一樣，既不影響產品精度，又能筒化設計程序，也有利于設計系數的推導。

2.3 系數設計法的推導

2.3.1 孔型內接正方形邊長ai及其設計系數λi

由變形過程中孔型內接正方形邊長ai與成品管邊長a及弓形高hi的幾何關系可以得出

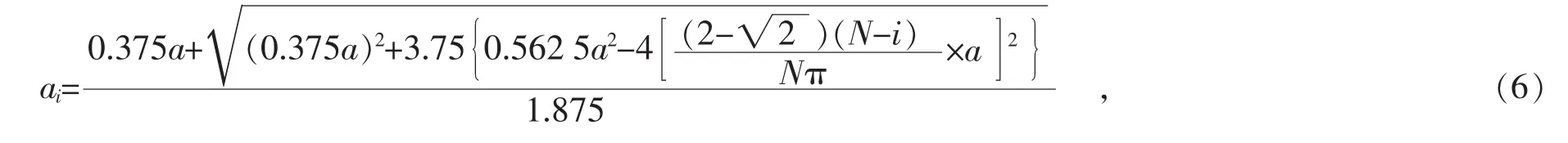
將 （6）式兩邊同除以a，并令ai/a=λi，得出

式 （7）的幾何意義是：當N確定之后，第i道次關于ai的設計系數λi便唯一確定；因此，決定函數大小的真正變量是正方形邊長。它的實際意義是，無論成品方管邊長如何變化，只要總變形道數N一定，第i道次孔型內接正方形邊長的設計系數就是定值；并且，在計算第i道次孔型內接正方形邊長時，只需將該系數與成品方管邊長相乘即可。

2.3.2 孔型變形半徑Ri及其設計系數μi

根據圓變方過程中孔型變形半徑Ri、孔型內接正方形邊長ai與弓形高hi的幾何關系可以得出

將（5）式和（6）式同時代入（8）式，且兩邊同除以成品方管邊長a，并令Ri/a=μi，得出

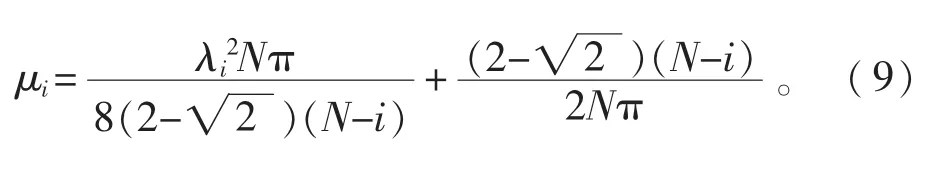
在（9）式中，設計系數λi是一個定值，一旦N的數值確定之后，圓變方過程中關于各道次變形半徑Ri的設計系數 μi亦就會為定值,Ri=μia。這樣，在進行第i道次變形半徑設計時，再無需進行繁瑣的運算了。

2.3.3 孔型寬和孔型深

由圓變方孔形之間的幾何關系，容易推導出孔型寬度和孔型深度是一個關于系數μi的表達式與方管邊長之積。圖1所示箱式孔型的孔型寬和孔型深由式 （10）決定。

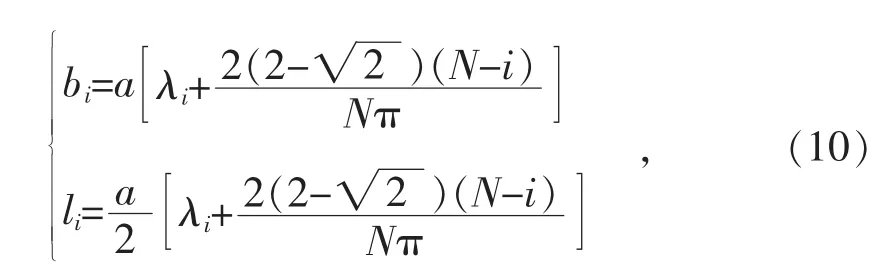
式中：bi—圓變方箱式孔型第i道次的孔型寬度；

li—圓變方箱式孔型第i道次的孔型深度。

若是斜出45°方管孔型，則其孔型寬和孔型深由（11）式確定。

式中：Bi—圓變方斜出45°方管第i道次孔型的寬度；

Hi—圓變方時斜出45°方管第i道次孔型的深度。

需要指出的是，（10）式也是“系數與方管邊長相乘”的形式，在N確定之后，第i道次的數值也是可以固化的。

2.3.4 圓變方孔型設計系數表

通常采用5平4立9個道次孔型軋輥完全能滿足各種規格圓變方管的軋制，即N=9，i=1，2，…，9。 那么，根據（7）式和（9）式，易得系數 λi和 μi。 圓變方9道次孔型設計系數見表1。有了這些系數后，就使得原本復雜的孔型設計過程變成了簡單四則運算，從而實現了圓變方孔型的 “傻瓜式”設計。

表1 圓變方9道次孔型設計系數

3 設計驗證

以設計圓變45方為例進行設計驗證。按5平4立9個道次、斜出45°設計變形孔型，則a=45 mm，N=9，i=1，2…，9。

3.1 系數設計法的設計實例

根據圓變方孔型系數設計法的設計思路、設計原則及表1所列設計系數，計算得圓變45方管孔型的變形參數，見表2；設計成果如圖2所示。

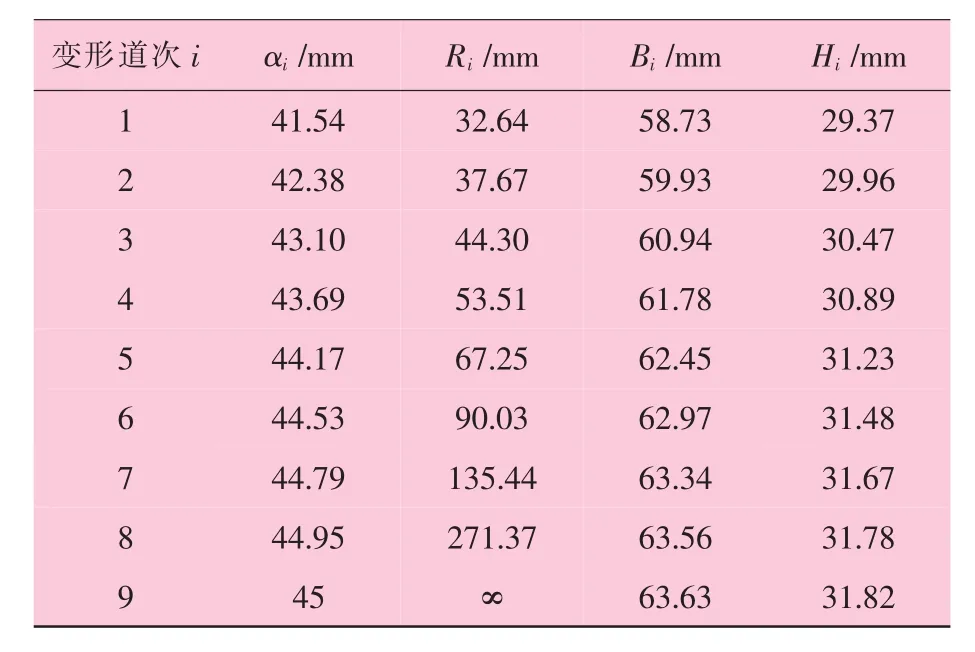
表2 圓變方系數設計法45方斜出45°孔型參數

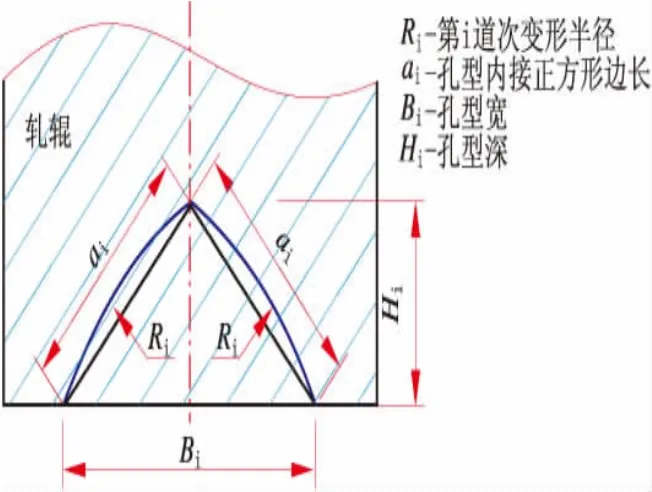
圖2 圓變方軋輥孔形圖

3.2 非系數設計法的設計實例

根據設計原則和（1），（2），（4），（5），（6）式及（8）式，并假設N=9，那么，圓變方非系數設計法45方、斜出45°孔型參數列見表3。

表 3 中，ai′、 Ri′、 Bi′、 Hi′分別表示圓變方非系數設計法45方斜出45°孔型第道次內接正方形邊長、變形半徑、孔型寬和孔型深。比較表2和表3的設計結果，系數設計法的數值與非系數設計法的數值，絕大部分完全一致，極少不一致的屬于計算精度誤差，這說明圓變方孔型的系數設計法正確可行。

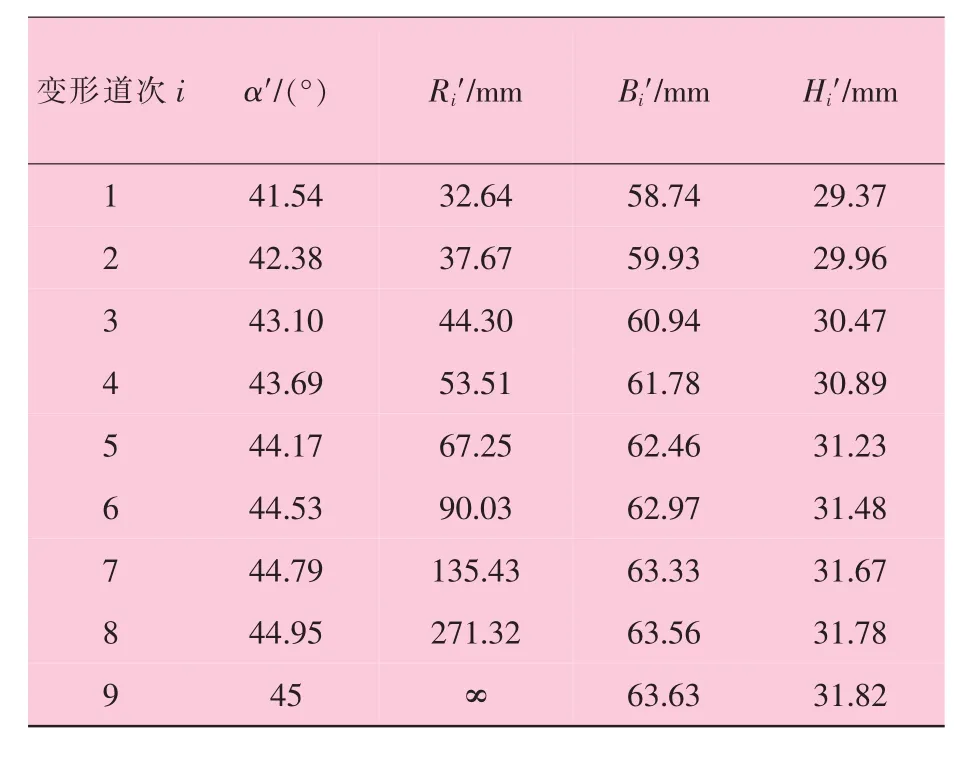
表3 圓變方非系數設計法45方斜出45°孔型參數

另一方面，雖然表2的設計思想和設計方法與表3不同，但是，兩個表內相同道次的相應數據幾乎一致的情況說明，圓變方孔型的參數，確實存在（7）式、（9）式和表1所顯示的內在系數規律。其數值精度完全能夠滿足焊管尺寸精度對孔型精度的要求。

3.3 反推的設計系數 μi′和 λi′

基于表3的設計結果和比照 （7）式、（9）式，易類推出由非系數設計法孔型參數反推的設計系數 μi′和 λi′，見（12）式和（13）式,

式中：λi′—非系數設計法反推出關于第i道孔型內接正方形邊長ai′的設計系數。

式中： μi′—非系數設計法中反推出的關于第道孔型變形半徑Ri′的設計系數。

那么，由（12）式和（13）式計算得，第i道次反推的系數 μi′和 λi′，詳見表 4。

表4 非系數設計法圓變方9道次孔型反推的設計系數

表4所顯示的反推系數μi′和 λi′與表1所列出的推導系數μi和λi基本相同，相同道次的對應系數都十分接近，其最大誤差均不超過萬分之二。這種 “十分接近”的結果表明：圓變方孔型系數設計法所推導出的孔型設計系數正確可信。反推系數與推導系數的唯一區別在于：前者是圓變方非系數設計法過程的終點，僅起驗證后者的作用；而后者則是圓變方系數設計法過程的起點，并貫穿圓變方孔型系數設計法全過程，是系數設計法的靈魂。

4 結 論

圓變方孔型的系數設計法不僅正確可行，而且能提高設計效率、避免設計風險，所得設計系數對所有圓變方孔型都適用。

（1）圓變方孔型系數法正確可行。系數設計法所推導出的系數與非系數設計法反推的系數高度一致，其數值精度完全能夠滿足焊管產品對孔型精度的要求。這種異曲同工的結果證明，圓變方之系數設計法的正確性。

（2）圓變方孔型的設計系數唯一。由于圓變方之圓直徑與方管邊長存在著固定系數關系和替代關系，這就為通過一定的數學變換，將代表各道孔型各部位曲線的函數表達式，演繹成系數與成品方管邊長相乘的形式提供了充分必要條件。而且，一旦N確定后，經過演繹獲得的各道次設計系數μi和λi，對所有圓變方孔型都具有唯一性；也就是說，在總變形道數N相同的情況下，不論成品方管規格如何變化，所有圓變方孔型第I道次的設計系數都相同，而且固定不變。

（3）提高設計效率。用系數設計法設計圓變方孔型，不再需要計算方管展開長度、初始圓直徑、總變形量、平均遞減變形量等繁瑣數據，直接根據系數與成品方管邊長的關系，計算圓變方孔型各部位的變形尺寸，從而簡化圓變方孔型設計程序，減少計算量，提高設計效率。同時，由于系數設計法不需要人為設定變形參數，這就從根本上避免了因設計人員經驗差異而可能產生的實際變形風險，使圓變方孔型的標準化設計成為現實。

另外，本研究提出的設計思路、設計原則和設計方法，對設計其他孔型亦有借鑒作用。

［1］曹國富.標準平橢圓管孔型的系數設計法［J］.鋼管，2013（06）：30-34.

［2］樊映川.高等數學講義（上冊）［M］.北京：人民教育出版社，1958.

［3］曹國富.采用公稱尺寸法設計異型軋輥孔型［J］.鋼管，2005，34（03）：23-27.

［4］首鋼電焊鋼管廠.高頻直縫焊管生產［M］.北京：冶金工業出版社，1982.

［5］張有文，段建平.方矩形管軋輥孔型設計［J］.陜西機械，2000（S2）：59-61.

［6］王先進.冷彎型鋼生產及應用［M］.北京：冶金工業出版社，1994.

［7］曹國富.簡析影響焊管質量的帶鋼增量［J］.上海金屬，1995，17（04）：50-53.

［8］羅濤,李銀.頂管機孔型設計與機架排列優化及實踐[J].鋼管,1993（04）：26-29.

［9］劉松泉.周期軋管機的孔型設計[J].鋼管，1988（01）：31-33.

［10］李激光,耿申初.重軌計算機輔助孔型設計[J].鞍山鋼鐵學院學報，1999（06）：41-44.