響水澗抽水蓄能機組軸系穩定性分析
李 巍,周佳亮,彭曉輝,楊國昌,程浩嵐,岳 衛
(哈爾濱電機廠有限責任公司,哈爾濱 150040)
1 軸系有限元建模
1.1 轉子本體
大型抽水蓄能機組軸系本體主要由上接軸、發電-電動機軸、電機轉子、水泵-水輪機軸、轉輪等組成。由于電機轉子的轉動慣量大,軸比較粗短,并且為空心軸,所以,在建模中考慮了陀螺效應和剪切效應。電機中心體作為軸的一部分來處理。轉輪的彎曲剛度很大,形狀復雜,可用厚壁圓筒代替。
1.2 導軸承與支撐結構
大型抽水蓄能機組一般有三個導軸承,均為有潤滑的可傾瓦式滑動軸承。導軸承油膜的動力特性系數一般通過求解 Reynold方程,得到油膜的壓力分布,再經過數值積分求得動力系數。油膜力與位移和速度的線性化關系式如下:

機組在穩定工況下運行,假設作用在軸頸上的油膜力與位移和速度的擾動為線性關系,油膜的剛度系數K和阻尼系數C可視為常數。但如果計算軸系在各瞬態工況時的動力響應,須考慮油膜力的非線性影響。
支撐剛度包括導軸承油膜剛度、支撐結構及混凝土基礎的剛度。電機上下支架的徑向剛度、水泵-水輪機頂蓋的徑向剛度及軸承的結構剛度均可由有限元分析精確得到。通常主要動載荷與機組轉速同步,支撐結構的第一階固有頻率遠遠高于要求機組達到的臨界轉速,因此支撐結構的剛度可用其靜剛度替代。另外,油膜剛度是隨著軸承負荷而變化的,為安全起見,在計算軸系臨界轉速時,通常在油膜動力系數和支撐剛度計算的基礎上,結合設計經驗來確定各導軸承與支撐結構的最低極限當量剛度。因此軸承的支撐結構可模化為彈簧與阻尼組成的系統。實際計算臨界轉速時,阻尼可忽略不計。
1.3 偏心磁拉力
當電機轉子偏離中心時,轉子與定子之間將產生偏心磁拉力,其大小與偏心量大致成正比。力學上可作為彈簧支撐,彈簧系數取負值。電磁計算可提供偏心磁拉力系數。
1.4 轉輪水的附加質量
轉輪內部的水是作為慣性參與軸系的振動。附加質量的大小一般根據經驗公式算取。
此外還有其他因素會影響軸系的動力特性,例如,推力軸承、轉子輪輻的彈性、轉輪的密封等。一般來講,由于它們的影響不大或不考慮是偏于安全的,因此可以不計。
2 編寫計算軸系臨界轉速及動力特性的命令流程序
在使用ANSYS程序計算轉子動力學問題時,如果考慮轉子隨轉速變化的陀螺效應,須采用命令流的方式。本文采用ANSYS的APDL語言編寫了前處理程geom.inp和臨界轉速及動力特性的自動求解程序shaftsolv.inp。
3 實例計算
電機軸的外直徑:1150mm;水泵-水輪機軸的外直徑:1150mm;電機轉子質量(不含軸):344t;電機飛輪力矩GD2:14000t·m2;轉輪質量:55t;轉輪飛輪力矩 GD2:750t·m2;電機轉子/轉輪平衡精度:3.2/6.3;額定工況轉輪徑向不平衡水推力:265334N;額定工況磁拉力系數:0.206MN/mm;額定轉速/飛逸轉速:250/375r/min。
4 軸系臨界轉速計算
響水澗抽水蓄能機組軸系的有限元模型見圖 3。上導軸承、下導軸承和水導軸承的彈性系數分別為:
α上= 1.667mm/MN;α下= 0.667mm/MN;α水=1.000mm/MN
上述導軸承的彈性系數是綜合了油膜彈性系數、支撐彈性及混凝土彈性的基礎上,結合設計經驗來確定的當量彈性。
計算結果見表1。圖2和圖3分別是有、無磁拉力作用時臨界轉速的Campbell圖。

表1 第一階臨界轉速 單位:r/min

圖1 響水澗抽水蓄能機組軸系的有限元模型
響水澗抽水蓄能機組的臨界轉速是 375r/min,無磁拉力時的臨界轉速是飛逸轉速的1.57倍,有磁拉力時的臨界轉速是飛逸轉速的1.48倍,滿足設計要求。

圖2 響水澗抽水蓄能機組軸系臨界轉速(有磁拉力)

圖3 響水澗抽水蓄能機組軸系臨界轉速(無磁拉力)
5 導軸承的油膜彈性
導軸承油膜彈性系數及阻尼系數是分析和優化發電機組軸系動態特性所必須的重要參數。本文給出了額定轉速和負荷的工況,機組在正常連續運行(熱態)和起動狀態(冷態)下,各導軸承油膜彈性系數和軸頸偏移的曲線,如圖4、圖5和圖6所示。從圖中可以看出油膜彈性與負荷的關系是非線性的。冷態的油膜彈性大于熱態的油膜彈性。


圖5 下導軸承油膜彈性及軸頸偏移

圖6 水導軸承油膜彈性及軸頸偏移
6 軸系受強迫振動引起動態響應
如前所述,由于導軸承油膜彈性與負荷、轉速等因素的非線性關系,對于三個導軸承支撐的非靜定結構要計算軸系的響應須采用迭代的方法。在計算模型中假設導軸承的初始彈性為計算臨界轉速時的值。考慮求解的是最大的負荷,由發電機和轉輪產生的橫向力取相反方向。
6.1 質量、電氣以及水力不平衡量
電動機-發電機的不平衡量:42kg·m
轉輪的不平衡量:13 kg·m
偏心磁拉力:576.8kN(靜態+動態,額定工況)
水力不平衡力:265.3kN(靜態+動態,額定工況)
參考其他機組的數據,穩定的飛逸工況(Stabilized Runaway speed),其水力不平衡力是額定工況的2倍,瞬態過速工況(Transient Over-speed),其水力不平衡力是額定工況的 5倍。另外,本文計算中,偏心磁拉力和水力不平衡力均按動態負荷考慮,這也是偏于保守的。
6.2 頻響函數
軸系上導、下導、水導和轉輪中心徑向位移的頻響曲線見圖7。
6.3 各運行工況的動態響應
額定工況穩定運行時,各導軸承的負荷見表2。穩定的飛逸工況時, 各導軸承的負荷見表3。瞬態的過速工況時,各導軸承的負荷見表4。額定工況穩定運行時,軸在各導軸承處的相對振幅以及轉輪中心的絕對振幅見表5。

表2 額定穩定運行工況導軸承負荷 單位:kN

表3 穩定的飛逸工況導軸承負荷 單位:kN

表4 瞬態的過速工況導軸承負荷 單位:kN

表5 額定穩定運行工況導軸承相對振幅和轉輪的絕對振幅 單位:mm
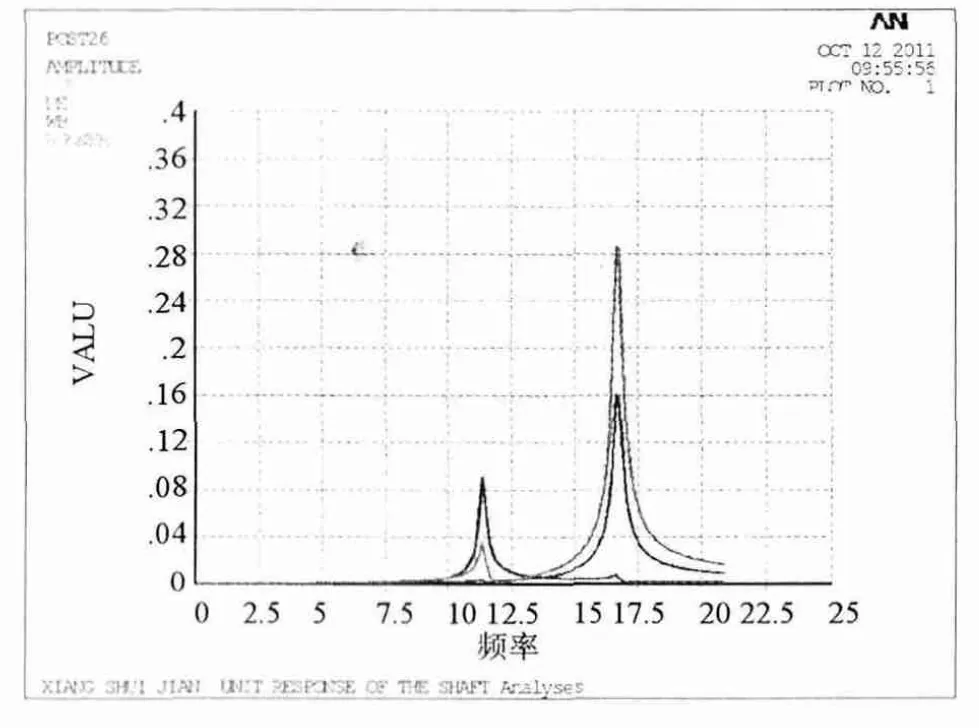
圖7 NDE-上導,DE-下導,WB-水導,RUNNER-轉輪
7 軸系扭轉振動固有頻率和瞬態動力響應
7.1 軸系扭振固有頻率
為防止因水力擾動而產生扭轉共振,須計算軸系的扭振固有頻率。一般只考慮第I階的固有頻率。該機組軸系的第I階扭轉固有頻率是14Hz,其振型如圖8所示。

圖8 軸系第I階固有頻率及振型
7.2 二相短路
電動機工況和發電機工況短路時產生瞬態電磁轉矩激勵比較接近,因此本文僅提供發電機工況的時間歷程圖。兩相短路時其電磁轉矩的時間歷程見圖9,轉軸關鍵部位的扭矩(響應)如圖10~圖12所示。表6給出軸系關鍵部位的最大扭矩。

圖9 發電機兩相短路時的電磁轉矩
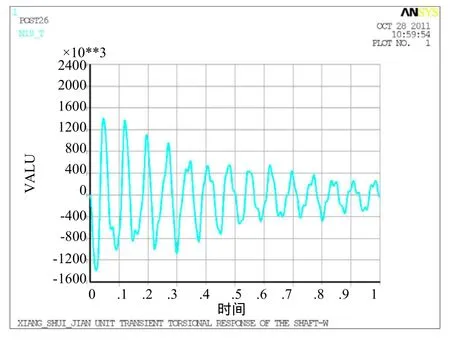
圖10 發電機兩相短路時轉子與發電機軸聯結法蘭處的扭矩

圖11 發電機兩相短路時發電機軸與水輪機軸聯結法蘭處扭矩

圖12 發電機兩相短路時水輪機軸與轉輪聯結法蘭處的扭矩
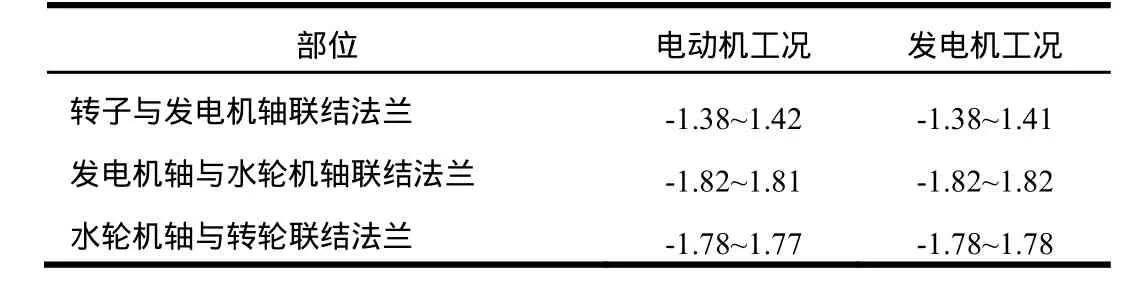
表6 兩相短路時軸系關鍵部位最大扭矩單位:MN·m
7.3 三相短路
三相短路時產生瞬態電磁轉矩激勵,其電磁轉矩的時間歷程如圖13所示。發電機工況三相短路時,軸系關鍵部位的扭矩(響應)如圖14~圖16所示。表7給出軸系關鍵部位的最大扭矩。

表7 三相短路時關鍵部位的最大扭矩單位:MN·m

圖13 發電機工況三相短路時的電磁轉矩

圖14 發電機工況三相短路時轉子與發電機軸聯結法蘭處的扭矩

圖15 發電機工況三相短路時發電機軸水輪機軸聯結法蘭處的扭矩
以上扭矩只是短路電磁扭矩產生的,計算應力和校核螺栓時須加上額定轉矩。最大額定扭矩在發電機工況為10.620MN·m。
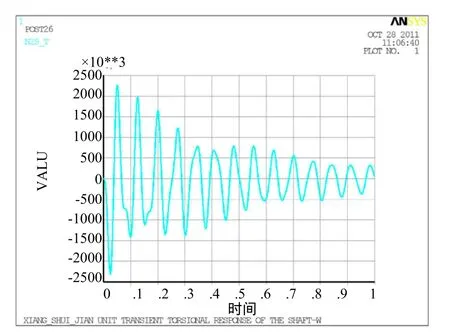
圖16 發電機工況三相短路時水輪機軸與轉輪聯結法蘭處的扭矩
8 結論
響水澗抽水蓄能發電機組是首臺自主研發、設計和制造的機組。本文比較系統地介紹了機組軸系的穩定性分析的過程。導軸承的動態載荷與油膜彈性的非線性關系,可為動力響應計算提供必要的數據。
在軸系動力響應分析中,計算了質量不平衡、電氣不平衡以及水力不平衡對軸系穩定性的影響,各導軸承處的橫向振動幅值均滿足ISO7919-3的振動標準的要求,同時也滿足設計標準規定。在兩相和三相短路工況時,軸系軸段及連軸器也滿足設計要求。認為機組在所計算的工況中是穩定的。

