不同功率同步電機瞬態時間常數的對比研究
許國瑞,劉曉芳,羅應立,宋美紅
?
不同功率同步電機瞬態時間常數的對比研究
許國瑞1,劉曉芳1,羅應立1,宋美紅2
(1. 華北電力大學電氣與電子工程學院,北京 102206;2. 中國·城市建設研究院,北京100120)
受電力系統安全生產要求的限制,通常采用小功率電機模擬并研究大型發電機的瞬態特性,但小功率電機定轉子電阻的標幺值并非遠小于相應繞組漏電抗,如果直接采用忽略電阻的傳統瞬態時間常數解析法對電機瞬態特性進行分析,必然產生一定誤差。為解決這一問題,本文推導了計及定轉子電阻的瞬態時間常數改進解析表達式,通過7.5kW模型機試驗及時步有限元方法驗證了該解析表達式的正確性,并將其應用于不同功率電機,發現當定轉子電阻變化相同倍數時,利用改進表達式計算瞬態時間常數的精度明顯高于傳統方法。研究結果為瞬態時間常數的計算和精確測量提供理論基礎。
小功率電機;瞬態時間常數;定子電阻;轉子電阻;時步有限元
0 前言
為了保證電力系統的安全生產和運行管理,對大型電機進行試驗測試和試驗研究要慎重。實驗室通常采用與大型電機相同結構等比例縮放的小功率同步電機模擬和研究大型發電機的動態特性[1-4]。然而與大型發電機相比,小功率同步電機定轉子電阻的標幺值并非遠小于相應繞組漏電抗,如果在計算小功率電機瞬態時間常數時仍然采用忽略定轉子電阻的傳統解析方法進行計算分析,必然會產生一定的誤差。因此,探討傳統計算大型發電機瞬態時間常數的方法能否直接用于計算小功率電機的動態特性是十分必要的。
在研究大型電機動態過程時,由于定轉子電阻標幺值相對于其漏抗很小,因而直軸瞬態時間常數的解析表達式中通常將定子電阻忽略,定子非周期瞬態時間常數的解析表達式中通常將轉子電阻忽略[5-8]。同樣,在對小功率電機進行動態研究時,部分文獻也采用這種忽略電阻的方法[9],例如突然加負載時的動態過程[10]。而小功率電機具有定轉子電阻值偏大而漏抗值偏小的特點[11-12],因此定轉子電阻對瞬態時間常數的影響仍值得進一步研究。
同步電機的瞬態參數是基于三相突然短路定義的,是描述電機瞬態和動態行為的重要參數[13-14]。三相突然短路試驗是測取同步電機瞬態參數較為理想的方法,也是國家標準[15]推薦采用的方法。因此本文主要基于空載三相突然短路對瞬態時間常數進行研究。
本文首先推導了空載三相突然短路后計及定轉子電阻的勵磁電流和瞬態時間常數的改進解析表達式,然后通過7.5kW模型機試驗及時步有限元驗證了該改進解析式的正確性,最后將該解析式用于不同功率電機,計算了不同定轉子電阻時電機的瞬態時間常數,得出改進解析式的計算精度明顯高于傳統解析式。研究結果為瞬態時間常數的計算和精確測量提供理論基礎。
1 瞬態時間常數的研究方法
1.1 傳統解析表達式
電力系統分析以及電機瞬態理論中對瞬態時間常數定義如下[11]:
傳統的直軸瞬態時間常數如式(1)所示:
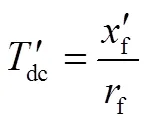
式中:f'為當轉子僅有勵磁繞組,且電樞繞組短路時從轉子繞組端看的瞬態電抗,f為勵磁繞組的電阻。
傳統的定子非周期衰減時間常數如式(2)所示:
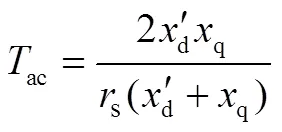
式中:d'為軸的瞬態電抗,q為交軸同步電抗,s為定子電阻。
空載三相突然短路勵磁電流的傳統表達式為:

電力系統常用的2到6階實用模型[16]均采用傳統方法得到的dc',ac。
1.2 改進解析表達式
為了研究瞬態時間常數與定轉子電阻的關系,在文獻[11]的基礎上,推導出了計及定、轉子電阻的勵磁電流改進表達式,得出了改進的直軸瞬態時間常數和定子非周期衰減時間常數的表達式。推導過程中忽略阻尼繞組。推導過程中采用運算電抗求解,直軸運算電抗與電機轉速無關,因而可以用來研究任何轉速時電機的各種運行工況,其表達式如下:
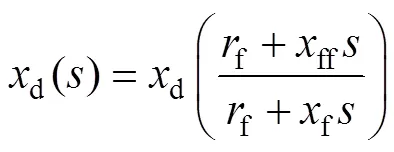
式中:d為直軸同步電抗,ad為直軸電樞反應電抗,f為勵磁繞組的電阻。
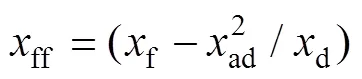
同樣,在忽略阻尼作用的情況下,交軸運算電抗可表示為:
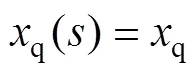
同步電機三相突然短路后軸電流的拉普拉斯變換式[11,17]為:
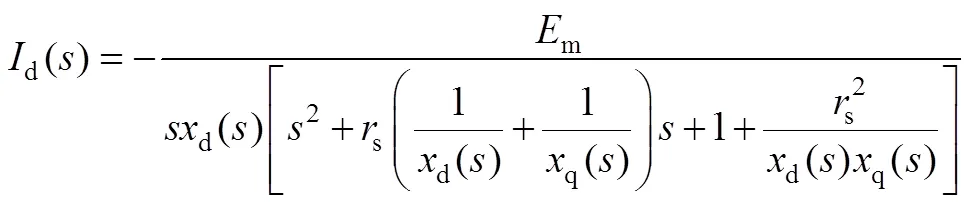
式中:m為空載電動勢的幅值。
勵磁電流的拉普拉斯變換式與軸電流的拉普拉斯變換式之間滿足如下關系:
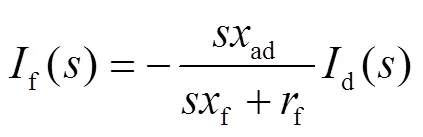
因此,勵磁電流的拉普拉斯表達式可變為:
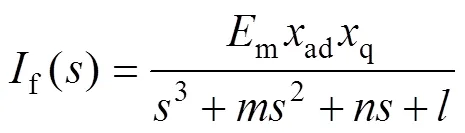
為對式(9)進行拉普拉斯反變換,需將分母因式分解,即令:
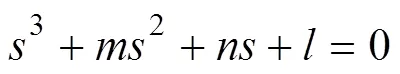
據卡丹公式[18]令(3)代入式(10)消去二次方得:
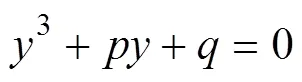
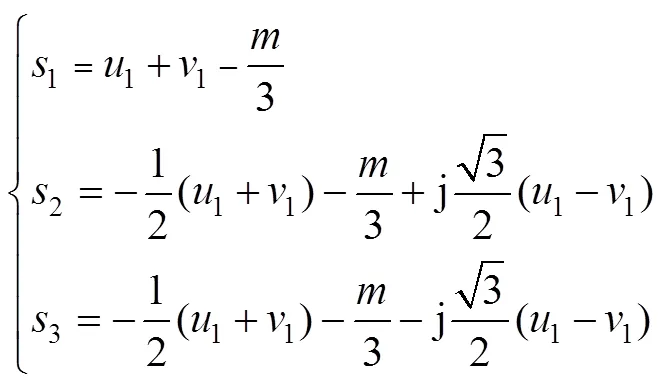
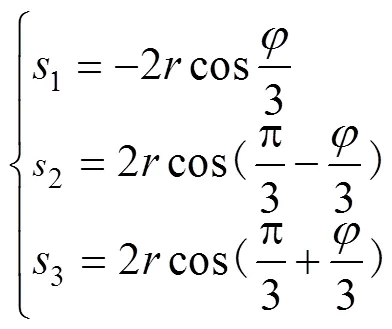
其中:
將勵磁電流進行拉普拉斯反變換后可以得到兩種勵磁電流的時域表達式:
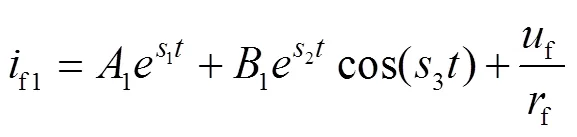
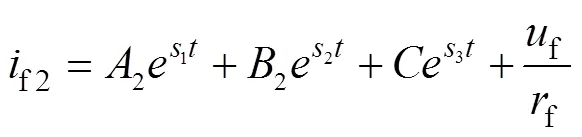
對比式(14)和式(15)可知,式(14)中既有交流衰減分量,又有直流衰減分量,而式(15)中只存在直流衰減分量。因此式(14)和(15)的直軸瞬態時間常數可表示為:
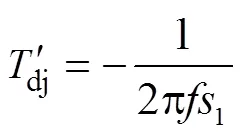
式(14)中存在定子非周期衰減時間常數,而式(15)沒有,因此式(14)中的定子非周期衰減時間常數可表示為:
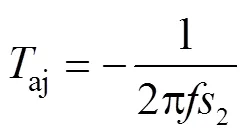
通過上述分析發現,計及定轉子電阻的勵磁電流改進表達式存在兩種形式,由此可知隨著定轉子電阻的不同,改進的瞬態時間常數也會發生變化。
1.3 時步有限元方法
1.3.1 時步有限元方法簡介
發電機的時步有限元模型(T-S FEM)能夠充分考慮發電機磁路飽和、磁場畸變、諧波磁場和集膚效應等作用,可為發電機動態運行工況提供標準響應[19]。時步有限元模型結合磁場方程與繞組回路方程得到[20],根據勵磁繞組各點電流密度的積分表達式,對各勵磁導體直線部分單獨列寫方程,再利用整個回路的電壓方程將其聯系起來,同時考慮電流的串聯約束條件,從而在計及勵磁繞組中渦流分布的情況下,準確計算發電機過渡過程中定子電流和勵磁電流的瞬態變化情況,為研究瞬態時間常數提供理論基礎。
1.3.2 時步有限元模型的實驗驗證
為了驗證該時步有限元模型的精確性,對一臺7.5kW模型機進行時步有限元仿真計算并與試驗進行對比,如圖1所示。
從圖1可以看出,7.5kW電機空載三相突然短路的時步有限元仿真與實測曲線非常吻合。時步有限元很好地計及電機內部的復雜非線性、磁場畸變等因素,它能有效地反映發電機穩態、暫態等運行行為,是一種比較精確的仿真工具。
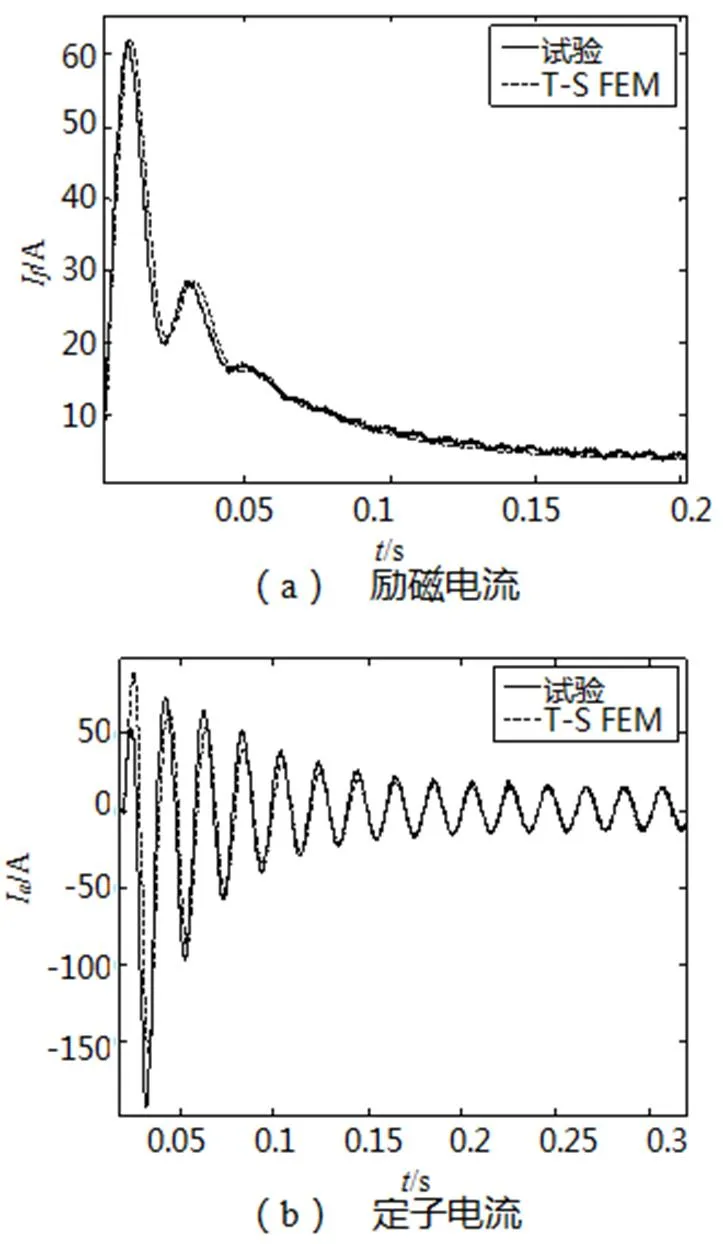
圖1 空載突然短路時時步有限元仿真與試驗對比
2 瞬態時間常數的對比分析
2.1 7.5kW同步發電機模型機
本文采用一臺兩極7.5kW同步發電機模型機對瞬態時間常數進行理論和試驗研究。模型機結構和樣機如圖2所示,表1為7.5kW模型機的參數。
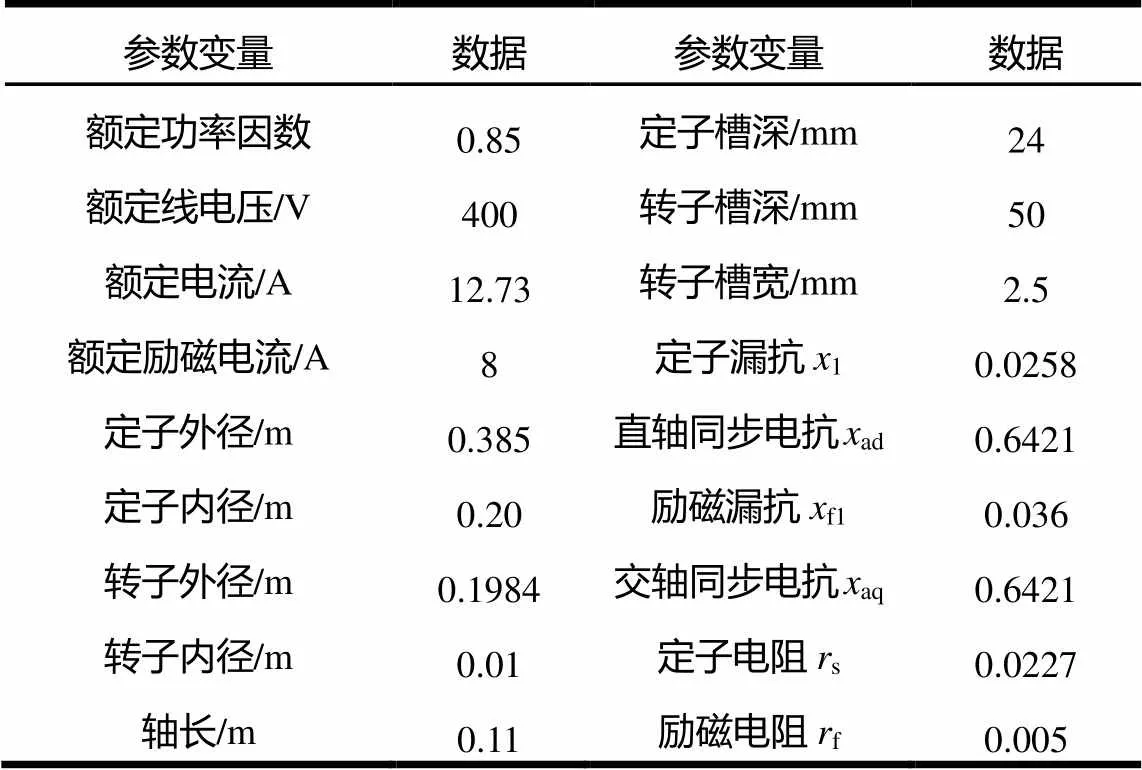
表1 7.5kW模型機基本數據
(a) 結構
(b) 樣機
圖2 7.5kW模型機
2.2 不同方法所計算瞬態時間常數的對比分析
采用時步有限元、改進解析表達式和傳統解析表達式計算7.5kW電機端電壓為110V時突然三相短路后的勵磁電流,結果如圖3所示。7.5kW電機的參數通過試驗測得[12],如表1所示。
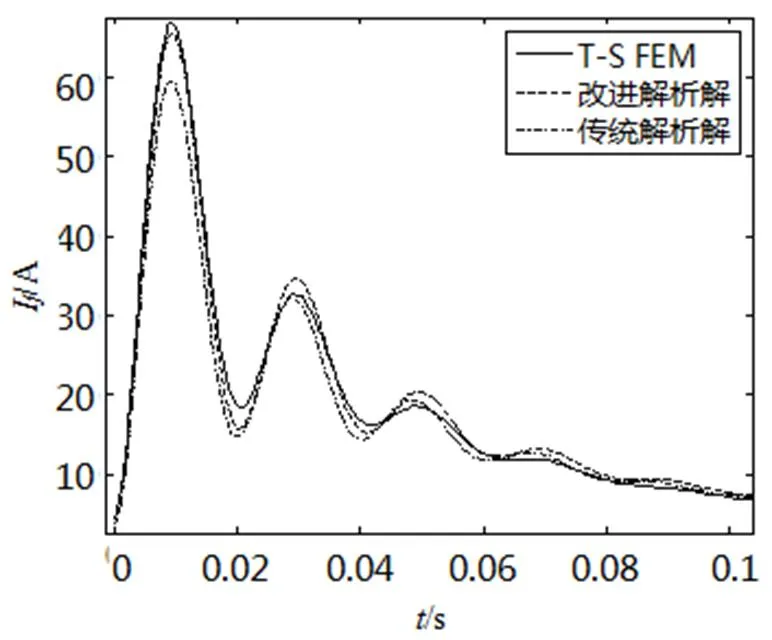
圖3 不同方法得到的勵磁電流對比
根據改進解析表達式和傳統解析表達式計算出空載三相突然短路勵磁電流,如式(18)和(19)所示。
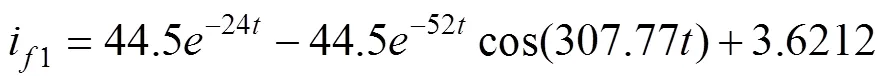
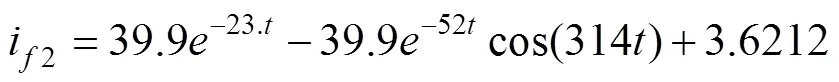
從上述兩式可以得出瞬態時間常數的改進解析解和傳統解析解,如表2所示。而從時步有限元計算的勵磁電流中無法直接獲得瞬態時間常數的大小,因此本文采用Prony方法[21]對時步有限元計算的勵磁電流曲線進行擬合,從而得出直軸瞬態時間常數和定子非周期衰減時間常數的數值。
對比圖3中的勵磁電流曲線和表2中的瞬態時間常數,得出改進解析表達式計算的勵磁電流曲線和瞬態時間常數與時步有限元結果更加接近,而傳統解析解與時步有限元相差較大。
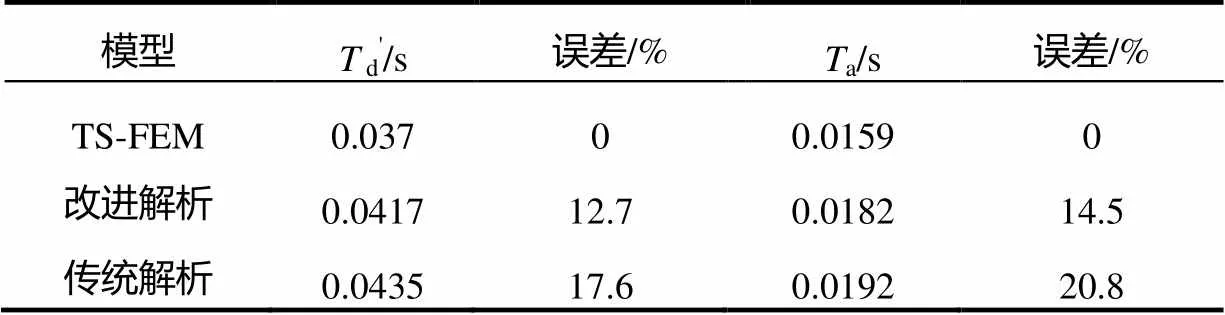
表2 不同方法得到的瞬態時間常數對比
2.3 定轉子電阻對瞬態時間常數的影響
為了研究定轉子電阻對瞬態時間常數的影響,在7.5kW電機定子三相繞組中串入阻值為4.286W的電阻,進行時步有限元仿真并與改進解析解和傳統解析解對比,得到勵磁電流響應曲線對比如圖4所示。
從圖4中可以看出,改進解析表達式計算的勵磁電流曲線與時步有限元結果更加接近。對時步有限元的勵磁電流曲線進行Prony擬合,得到直軸瞬態時間常數與改進解析解一致,約為0.12s,而傳統表達式計算的直軸瞬態時間常數不隨定子電阻的變化而變化,仍為表2所示的0.0435s。因此說明定子電阻的變化會影響直軸瞬態時間常數的大小,而傳統解析表達式不能計及這種影響。
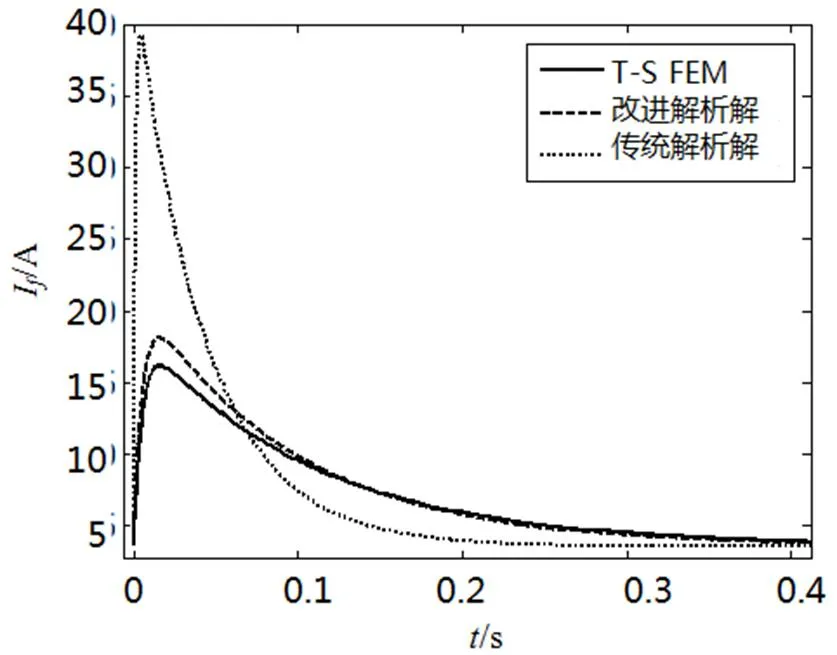
圖4 定子串電阻后的勵磁電流曲線
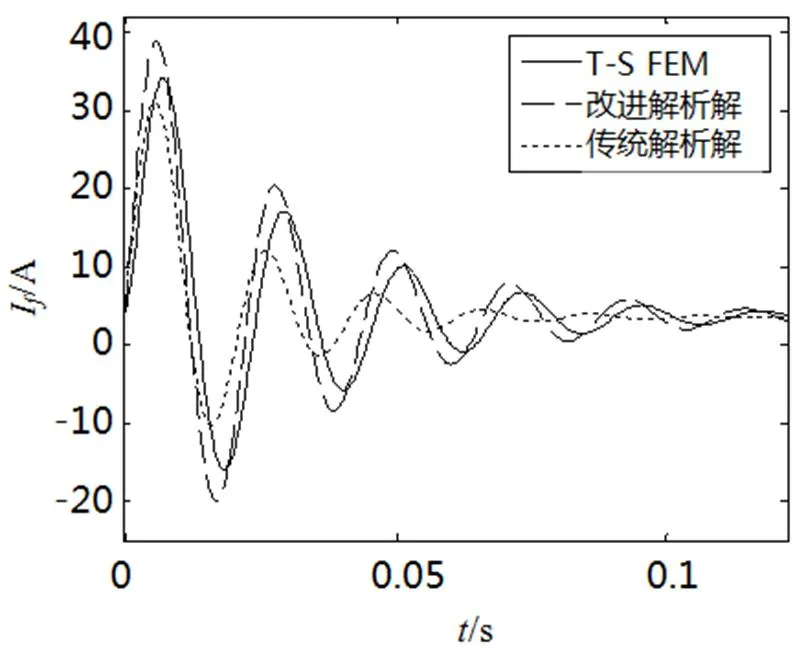
圖5 轉子串電阻后的勵磁電流
同樣,在轉子繞組中串入12.7W電阻后,采用時步有限元、改進解析表達式和傳統解析表達式計算的勵磁電流曲線如圖5所示。對時步有限元計算的勵磁電流曲線進行Prony擬合,得出定子非周期時間常數與改進解基本一致,約為0.023s,而傳統表達式計算的定子非周期時間常數不隨轉子電阻的變化而變化,仍為表2所示的0.0192s。因此說明轉子電阻的變化會影響定子非周期時間常數的大小,而傳統解析表達式不能計及這種影響。
2.4 瞬態時間常數改進解相對于傳統解的偏差分析
2.4.1 7.5kW同步電機
從文獻[11,12]可以得出,不同功率同步電機的定轉子電阻標幺值相差接近10倍。為了分析不同定轉子電阻大小情況下,瞬態時間常數的改進解與傳統解的差別,將7.5kW同步電機定轉子電阻在實際值的0.1~10倍范圍內進行變化,計算不同定轉子組合時直軸瞬態時間常數和定子非周期衰減時間常數的改進解相對于傳統解的偏差。改進解相對于傳統解的偏差和如式(20)和(21)所示。計算結果如圖6,7所示,圖中,軸為定轉子電阻的變化倍數,軸相對偏差,單位為%。
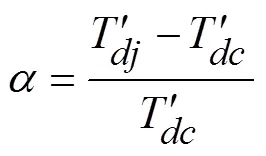

從圖6中可以看出,隨著定子電阻的增大,的絕對值在不斷增大。實際定轉子電阻下,值為2.5%,當定轉子電阻增大10倍時,變為53%。同樣,從圖7中可以看出,實際定轉子電阻下,值為0.6%,而當定轉子電阻增大10倍時,則變為181%。可見,對于小功率電機來說,瞬態時間常數的傳統解與改進解具有很大差別。
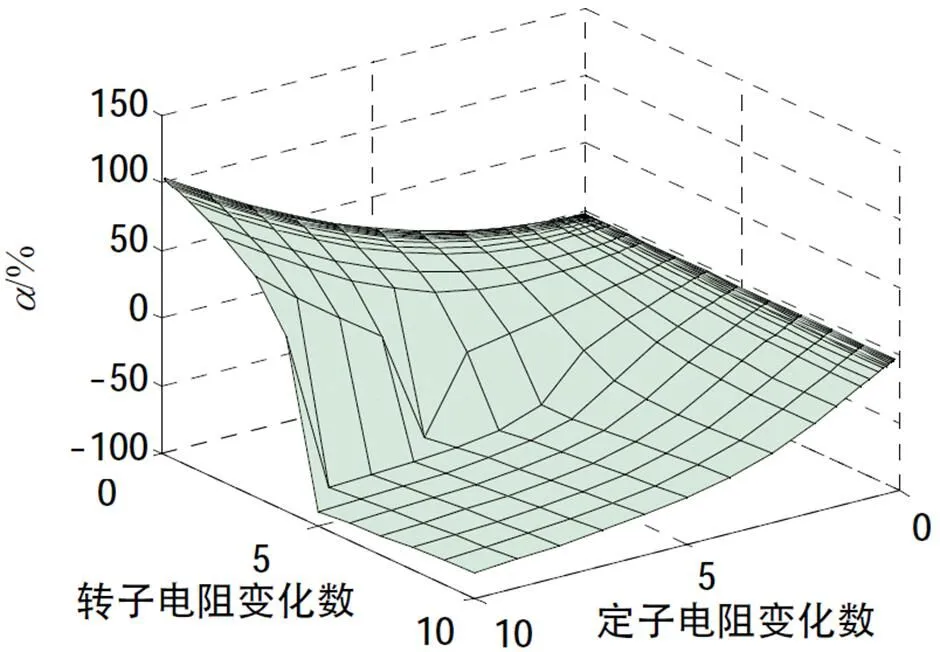
圖6 不同定轉子電阻時,Tdj'相對于Tdc'的偏差
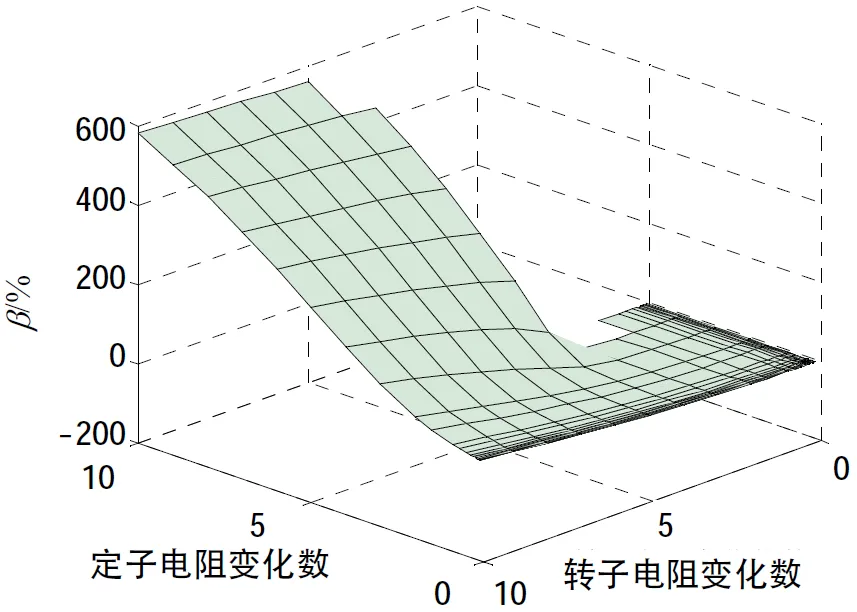
圖7 不同定轉子電阻時,Taj相對于Tac的偏差
2.4.2 300MW同步電機
采用與2.4.1節相同的方法,計算了300MW同步電機的定轉子電阻在10倍范圍內變化時,直軸瞬態時間常數和定子非周期衰減時間常數的改進解相對于傳統解的偏差。300MW同步電機的參數見文獻[11],通過計算得出,在10倍的定轉子電阻變化范圍內,直軸瞬態時間常數的改進解相對于傳統解的最大偏差為0.13%,而定子非周期衰減時間常數的改進解相對于傳統解的最大偏差僅為0.09%。因此,傳統法對大功率同步電機適用,但在小功率同步電機上會有一定偏差。此時采用改進解,更具有明顯精度優勢。
3 結論
本文通過理論推導和仿真對比的方法研究了定轉子電阻對小功率電機瞬態時間常數的影響,得出如下結論:
(1)采用改進表達式和傳統表達式計算了7.5kW電機的直軸瞬態時間常數和定子非周期衰減時間常數,并與時步有限元進行對比,得出改進解與時步有限元結果更接近,而傳統解則與時步有限元結果相差較大。
(2)通過計算不同定轉子電阻時,7.5kW電機與300MW電機瞬態時間常數改進解相對于傳統解的偏差,得出傳統方法對大型同步電機適用,但在計算小功率同步電機瞬態時間常數時與改進解具有明顯差異。此時采用改進解析表達式計算小功率同步電機具有明顯的精度優勢。
(3)在進行小功率電機的動態仿真和參數辨識時,必須考慮到定、轉子電阻的大小對瞬態時間常數的影響,這樣才能選擇恰當的模型從而得到更精確的結果。
[1] 王旭東, 王亞軍, 葛叢梅, 李哲生. 采用三相突然短路法測量同步電機參數[J]. 電機與控制學報, 1997, 1 (1): 14-17.
[2] 周茜, 蘇鵬聲, 王祥珩. 水輪發電機失磁的動態過程分析[J]. 電力自動化設備, 2002, 22(6): 9-11.
[3] 張侃君, 尹項根, 陳德數, 張哲, 楊德先, 吳彤. 大型多分支繞組水輪發電機動態模擬研究[J]. 電網技術, 2009, 33(6): 96-101.
[4] SAROJ RANGNEKAR, K. V. N. RAO, MAHENDRA KUMAR GUPTA, S. N. SAXENA. Development of Time Constant Regulator for micromachining[J]. IEEE Transactions on Industrial Electronics, 1985, 32(4): 410-413.
[5] L.A. KILGORE. Calculation of Synchronous Machine Constants- Reactance and Time Constants Affecting Transient Characteristics[J]. A.I.E.E.Trans, 1931.
[6] Fernando L.Alvarado, Claudio Canizares. Synchronous machine parameters from sudden-short tests by back-solving[J]. IEEE Transactions on Energy Conversion, 1989, 4(2): 224-230.
[7] 鞠平, 倪臘琴, 韓敬東, 陳新琪. 同步電機參數辨識的模擬進化方法[J]. 電工技術學報, 1999, 14(5): 1-4.
[8] L. Salvatore, Prof., Eng., and M. Savino, Prof., Eng. Experimental determination of synchronous machine parameters[J]. Mathematical techniques, IEEPROC, 1981, 128(4): 212-217.
[9] 康爾良, 王靖, 孫力. 大型發電機試驗數據分析和動態參數辨識[J]. 大電機技術, 2005, (4): 1-5.
[10] 湯曉燕. 同步電動機的動態和瞬態穩定極限[J]. 電機與控制學報, 2006, 6(4), 275-278.
[11] 馬志云. 電機瞬態分析[M]. 北京: 中國電力出版社, 2008.
[12] 許國瑞. 用于系統動態仿真的模擬電機參數及擾動特性研究[D]. 北京: 華北電力大學, 2010.
[13] 梁艷萍, 湯蘊璆. 大型汽輪發電機瞬態參數的數值計算[J]. 電工技術學報, 1999, 14(2): 5-11.
[14] 王亮, 王公寶, 馬偉明, 吳旭升. 基于小波變換和神經網格的同步電機參數辨識新方法[J]. 中國電機工程學報, 2007, 27(3): 1-6.
[15] 中華人民共和國國家標準, 三相同步電機試驗方法[S], GB/T 1029-2005.
[16] 倪以信, 陳壽孫, 張寶林. 動態電力系統的理論和分析[M]. 北京: 清華大學出版社, 2002.
[17] 高景德, 張麟征. 電機過渡過程的基本理論及分析方法[M]. 第一版. 北京: 科學出版社, 1982.
[18] 邢富沖. 一元三次方程求解新探[J]. 中央民族大學學報(自然科學版), 2003. 12(3): 207-218.
[19] 胡笳, 羅應立, 劉曉芳, 康錦萍. 汽輪發電機暫態分析中計及勵磁電流集膚效應的時步有限元模型[J]. 中國電機工程學報, 2008, 28 (30): 90-95.
[20] 羅應立, 胡笳, 劉曉芳, 王紅宇, 康錦萍. 面向系統動態分析的場路網耦合時步有限元模型. 中國電機工程學報[J]. 2009, 29(33): 102-110.
[21] 曹維, 翁斌偉, 陳陳. 電力系統暫態變量的Prony分析[J]. 電工技術學報. 2000, 15(6): 56-60.
Study on the Transient Time Constant of the Synchronous Generator with Different Capacity
XU Guorui1,LIU Xiaofang1, LUO Yingli1, SONG Meihong2
(1. North China Electric Power University, Beijing 102206, China;2. China Urban Construction Design &Research Institute, Beijing100120, China)
The small power synchronous generators are commonly used to simulate and study the transient response of the large generators, due to the restriction of the safety production in power system. However, the stator and rotor resistance in per unit of small power synchronous generator is much less than their leakage reactance; some error will be produced, if the traditional transient time constants which neglect the stator and rotor resistance are adopted. In order to solve this problem, this paper deduces the improved analytical expression of exciting current in the no-load and three-phase short circuit situation with the resistance of stator and rotor considered. The test and Time Step Finite Element Method (T-S FEM) of 7.5 kW model machine verify the correctness and validity of this model. The precision of the improved solution is higher than traditional solution with different value of the stator and rotor resistance. The result provides theoretical basis to calculate and test transient time constant accurately.
model machine; transient time constant; stator resistance; rotor resistance; time step finite element method
TM341
A
1000-3983(2014)01-0001-05
“十一五”國家科技支撐項目(2008BAA13B02)。
2013-10-13
許國瑞(1986-),華北電力大學電機與電器專業,研究方向為同步發電機模型及參數,博士研究生。

審稿人:李桂芬

