基于小波包Shannon熵的PHM系統故障特征提取

王 莉，劉 進，張 強，張丹旭

（空軍工程大學防空反導學院，西安 710051）

0 前言

針對傳統的“計劃維修”和“事后維修”在裝備維修保障中存在的嚴重不足。經常會造成資源的大量浪費，嚴重的可能造成人員傷亡和財產損失，本文將PHM系統應用到同步發電機維修保障系統中。

研究顯示信號特征提取是建立PHM系統的前提和基礎，直接關系到故障狀態識別的準確性和故障預測的可靠性[1]。傳統的信號處理方法有Fourier變換，但是其處理非線性時變信號能力較差。對于同步發電機，軸承故障信號復雜多變且有很強的背景噪聲，傳統的方法難以有效地提取信號中的有用信息。小波包變換是近年來應用廣泛的強有力的處理非平穩信號的工具，具有多分辨率分析的特點，而且在時域和頻域都具有表征信號局部特征的能力，信息熵理論中的Shannon熵抗干擾性較強。二者相結合能夠很好地處理軸承振動信號。因此，通過計算軸承振動信號的小波包熵來構造電機故障特征提取模型。

1 PHM系統

PHM系統是一種新興的集故障診斷、故障預測和健康管理能力于一體的綜合保障系統，是現有的機內測試（Built-in Test，BIT）故障診斷和健康管理的發展，它借助于智能化手段對關鍵部件的故障進行實時監控，同時預測關鍵部件的剩余壽命，使得系統在尚未完全故障之前人們就能依據系統的當前健康狀況決定何時維修，實現自助式保障，降低使用和保障費用[2]。工程應用及分析表明，采用PHM技術后，可以減少裝備停機時間，提高裝備的適用可用度，從而提高裝備的戰備完好率[3]。

PHM系統的功能有故障檢測、故障診斷、故障預測、故障影響評估和性能降級趨勢分析等。它的關鍵技術主要有新型的傳感器技術，高探測率的故障診斷技術，故障預測技術和先進的健康管理技術。典型的PHM系統工作流程如圖1所示，包括數據采集和處理、特征量提取、狀態檢測、故障診斷和故障預測環節。

圖1 PHM系統框圖

研究表明，PHM技術是在系統工作在可以接受的范圍內判斷未來時刻是否發生故障。因此要求系統對微小的故障信息要有足夠的分辨靈敏度。同時由于它所研究的故障征兆信號的幅值一般都很小，容易混雜在系統強背景噪聲中，因此要求系統的抗干擾能力要強。提取特征量的準確性直接影響故障診斷和預測的可靠性，因此對信號進行采集處理，有效地提取特征量是故障診斷和預測的前提和基礎。

2 軸承故障特征分析

軸承故障是同步發電機常見的故障之一，其故障率占總故障的30%～40%[3]。由于裝配不當、潤滑不良等因素會導致軸承過早出現故障。軸承故障一般從位于滾道和滾動體表面下的微小裂紋開始，并逐漸擴展，經過一段時間運轉，便會出現疲勞剝落和磨損，導致軸承不能正常工作。常見的軸承故障有內圈和外圈故障，如內圈或外圈出現點蝕、剝落或裂紋等。

當滾動軸承的某一元件表面存在局部故障時，在軸承的旋轉過程中，故障表面會周期性地撞擊滾動軸承其他元件的表面，從而產生間隔均勻的脈沖力。而周期性沖擊的頻率即為滾動軸承的故障特征頻率。實驗表明，軸承故障位置不同，故障特征頻率也不同，可以根據有無故障特征頻率和它幅值的大小來預測軸承發生何種故障及發生故障的程度。

軸承外滾道和內滾道磨損后的故障特征頻率計算公式為：

其中 fa為振動頻率，Z為滾珠數目，d為滾珠直徑，D為節徑，α為接觸角。

當滾動軸承內環的某個部位存在剝落、裂紋、壓痕、損傷等缺陷時，軸承內環故障的特征頻率為 fi及其高次諧波頻率；當滾動軸承外環的某個部分存在缺陷時，軸承外環故障的特征頻率為f0及其高次諧波頻率。研究表明，由于軸承本身結構特點，即使正常的軸承也有相當復雜的振動和噪聲。當軸承發生故障后，故障特征信號會被強烈的背景噪聲淹沒。故障特征信號的提取顯得尤為關鍵。而想要通過簡單分析軸承振動信號診斷故障相當困難。

3 基于小波包Shannon熵理論的軸承故障特征提取方法

小波包變換是一種基于“頻帶”的時頻分析方法，在高頻范圍內時間分辨率高，在低頻范圍內頻率分辨率高。它通過多層次劃分頻帶能夠進一步分解細分高頻部分，根據信號的特點，自適應地選擇合適的頻段，與信號頻譜相匹配，使頻譜窗口進一步分割變細，以提高信號的分辨率，適合于同步發電機的非平穩信號分析。

設正交小波基的濾波器系數分別為hn和gn，并將尺度函數φ(t)改記為w0(t)，小波函數ψ(t)改記為w1(t)，于是關于φ(t)和ψ(t)的方程變為[4]：

由式（2）定義的函數集合｛wn(t)｝n∈Z稱為由w0(t)=φ所確定的小波包。與小波分解相比，小波包變換增加了一個頻率參數n。它用w2n和w2n+1將Wj空間分為相對低頻和相對高頻的兩個子頻帶。通常對信號f作i次分解，一共可以分解得到的 N= 2i個子頻帶。

結合小波包和信息熵給出小波包熵的理論，設對信號進行 j層小波包分解可以得到節點系數Sjk,其中k=0，1，2……2j－1,設小波包系數的采樣點數為 N，由此得出第 i個子頻帶小波包節點系數對應的能量Ejk(i)。

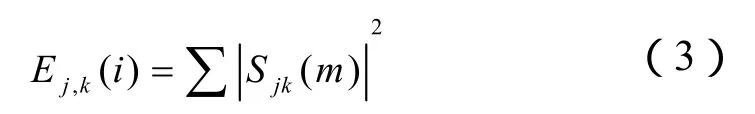
將各層子頻帶的節點系數能量作歸一化處理得

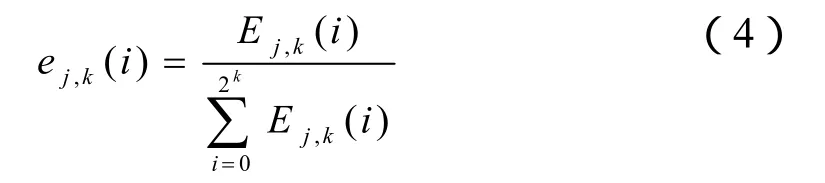
可以看出ej,k(i)是第 i個子頻帶包含的信息能量在j層小波包上總能量中的概率，根據Shannon信息熵的基本理論[5]，定義信號小波包分解的第j層k節點Sj,k的小波包熵Hj,k為

小波包Shannon熵理論是基于小波包分析方法建立起類似的信息熵理論，能夠發現信息中微小的異常變化，實現低信噪比條件下提取弱信號和消除噪聲，是對時頻域上的能量分布特性進行定量描述[6]。

當電機軸承發生故障時，信號中會出現相應的故障特征頻率，故障特征頻率的存在使信號不同頻段的能量發生變化。應用小波包熵理論分析故障電機振動信號，可以清楚地反映出故障特征頻率在信號不同頻段中的分布情況，通過與正常電機振動信號作對比，診斷、預測和定位軸承故障。

4 實驗驗證

本文以同步發電機軸承故障為例，在PHM系統中應用小波包熵理論提取故障特征構建故障特征提取模型，并以此為依據診斷、預測和定位故障。

選取3個型號一致的軸承，測得軸承的滾珠數目Z=7，滾珠直徑d=17.5mm，節徑D=72.5mm，接觸角α=0°。同步發電機轉速1500r/min，其轉動頻率為25Hz。其中2個軸承分別設置為內圈和外圈局部故障，1個為正常軸承。故障軸承在內圈和外圈上開槽，通過設置槽深槽寬的大小設置故障程度為輕微故障。中等故障和嚴重故障：以槽寬分別為0.2mm、0.4mm、0.6mm，槽深分別為0.3mm、0.6mm、0.9mm來表征故障程度。根據公式（1）可以計算出兩種故障情況下軸承的故障頻率為：外滾道故障特征頻率為66.38Hz，內滾道故障頻率為108.6Hz。圖2為正常情況和故障狀態下軸承振動的波形圖。

從圖2可以看出，軸承振動信號含有復雜的背景噪聲，有用的信息全部被淹沒在噪聲中，根本無法從圖中發現故障特征頻率，不能依靠振動波形來進行故障預測和診斷。

圖3為不同故障程度下的頻譜波形圖，從圖中可以看出不同故障之間故障特征頻率非常明顯，以此可以初步進行故障定位。但是同一故障，嚴重程度不同時在頻譜波形圖上反映不明顯，不能依靠振動信號頻譜來診斷故障嚴重程度。

圖2 振動波形圖

圖3 振動信號頻譜

因此本文對振動信號進行小波包分解，進而求取小波包Shannon熵值。

實驗選取db2小波對軸承振動信號進行4層小波包變換，可以得到（4，0），（4，1）……（4，15）共16個子頻帶，設采樣頻率1000Hz，則得到的頻帶頻率范 圍 為 （ 0～31.25Hz），（ 31.25～62.5Hz），（62.5～125Hz）……，根據公式（1）計算知軸承外滾道和內滾道故障特征頻率分別在（4，3）和（4，2）頻段內。仿真結果如圖3所示。

圖4 小波包分解

利用小波包熵理論計算正常狀態，輕微故障，中等故障和嚴重故障的小波包熵值，每種狀態的熵值分別計算10次，得出平均值列出表1。

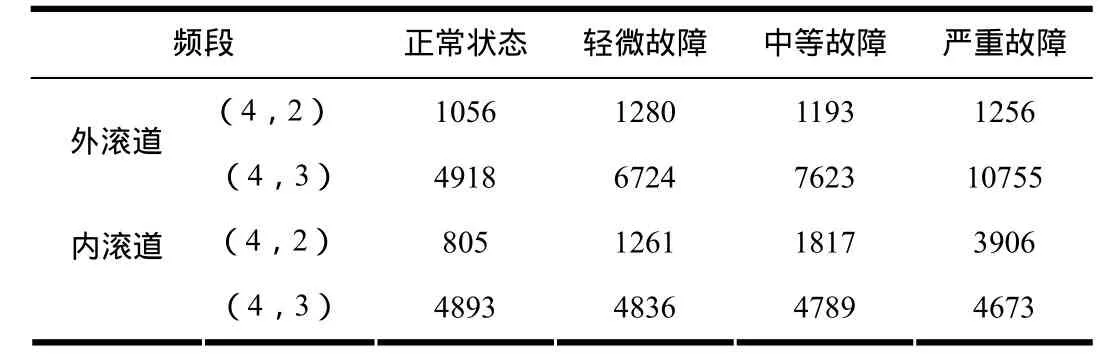
表1 小波包Shannon熵值

從表中可以看出，隨著故障嚴重程度增加，外滾道故障中的（4，3）頻段的小波包值變換明顯超過了30%，這是因為隨著故障嚴重程度增加，相應的故障特征頻率的幅值也變化明顯，導致相應的小波包頻段內的能量產生變化；（4，2）小波包頻段的熵值變化不大。而對于內滾道的（4，2）頻段來講，Shannon熵值變化率超過了40%，隨著故障程度變化十分明顯，（4，3）頻段的熵值變化卻不大。

由此為依據可以應用到同步發電機故障的嚴重程度預測和故障定位：

（1）以（4，2）和（4，3）頻段熵值變化率的大小進行故障定位。

（2）以正常軸承熵值為標準，設定閾值，進行故障嚴重程度診斷和故障趨勢預測。

5 結論

本文主要介紹了同步發電機 PHM 系統中故障特征提取的方法。以軸承的典型故障為例，提出了基于小波包Shannon熵的故障特征提取方法。經過實驗驗證，得出以下結論：

（1）小波包分析信號的方法可以有效消除同步發電機軸承振動信號中噪聲的干擾，準確提取故障特征。

（2）以小波包Shannon熵值作為故障特征表征量可以清楚地區分出軸承不同部位的故障。

當然，故障特征提取只是 PHM 系統的前提和基礎，真正實現故障預測和健康管理，必須以此為依據建立故障預測和診斷模型，這是以后研究的重點和難點。

[1] 曾慶虎.機械傳動領域關鍵零部件故障預測技術研究[D].長沙, 國防科技大學, 2010.

[2] 許麗佳.電子系統的故障預測與健康管理技術研究[D].成都, 電子科技大學, 2010.

[3] 劉瑞.基于PHM 的航空裝備可用度影響因素分析方法[J].北京航空航天大學學報, 2011, 37(10):1239-1241.

[4] 馬宏忠.電機狀態監測與故障診斷[M].北京: 機械工業出版社, 2008: 677.

[5] 張亞楠.基于小波包Shannon熵SVM和遺傳算法的電機機械故障診斷[J].電力自動化設備, 2010,30(1): 87-91.

[6] 胡鵬.基于小波包熵的船舶軸頻電場信號消噪研究[J].應用基礎與工程科學學報, 2011, 19(4):672-677.

[7] 安學利.基于ITD和LS-SVM的風力發電機組軸承故障診斷[J].電力自動化設備, 2010, 31(9):10-13.