中職數學中的函數教學技巧探討

摘 要： 函數是中職數學的基石，掌握函數概念、性質及常見類型，對理解后續內容有舉足輕重的影響。本文專注于函數教學內容、形式、技巧的探討，力求把函數與學生所學專業及生活實踐聯系起來，深入淺出、融會貫通，從而激發學生的學習興趣和學習積極性。

關鍵詞： 中職數學教學 函數 教學技巧

函數是中職數學的基石，掌握函數概念、性質及常見類型，對理解后續內容有舉足輕重的影響。然而，中職學生普遍對數學學習存在畏難情緒，覺得數學抽象難懂、枯燥乏味，難以與其他課程融合，更難以學以致用。筆者認為，在函數教學中，應把函數與學生所學專業及生活實踐聯系起來，深入淺出、融會貫通，從而激發學生的學習興趣和學習積極性。下面我就函數教學內容、形式、技巧作探討。

一、函數概念與表達形式

首先要讓學生明白函數的引入是人類認識事物的自然發展與要求，可以從生活與哲學兩方面引入。生活中可以用“日常生活中的一切事物都在不停地變化著，從街道上汽車的行駛到天空中的斗轉星移，從人的出生到老年到世界人口不斷膨脹，從銀行存款利息的逐漸增加到各種股票指數的漲漲落落，從加熱時壺中的水溫由20度到100度到全球氣候變暖”。我們關注身邊的這些變化著的事物，在數學上就是變量，而變化著的事物之間的依存關系，在數學上就是函數。馬克思主義哲學認為：事物是變化的，于是有了變量；事物不是孤立存在的，是相互聯系的，于是有了函數。也可以進一步說明這種相互聯系有兩種，一種是確定的，稱為函數關系；另外一種是不確定的統計關系，是偶然性與必然性的對立統一。兩者都可以舉一些生活中的例子加以說明，這樣就引入了概率論和統計學，并且能夠與函數概念相互區別。

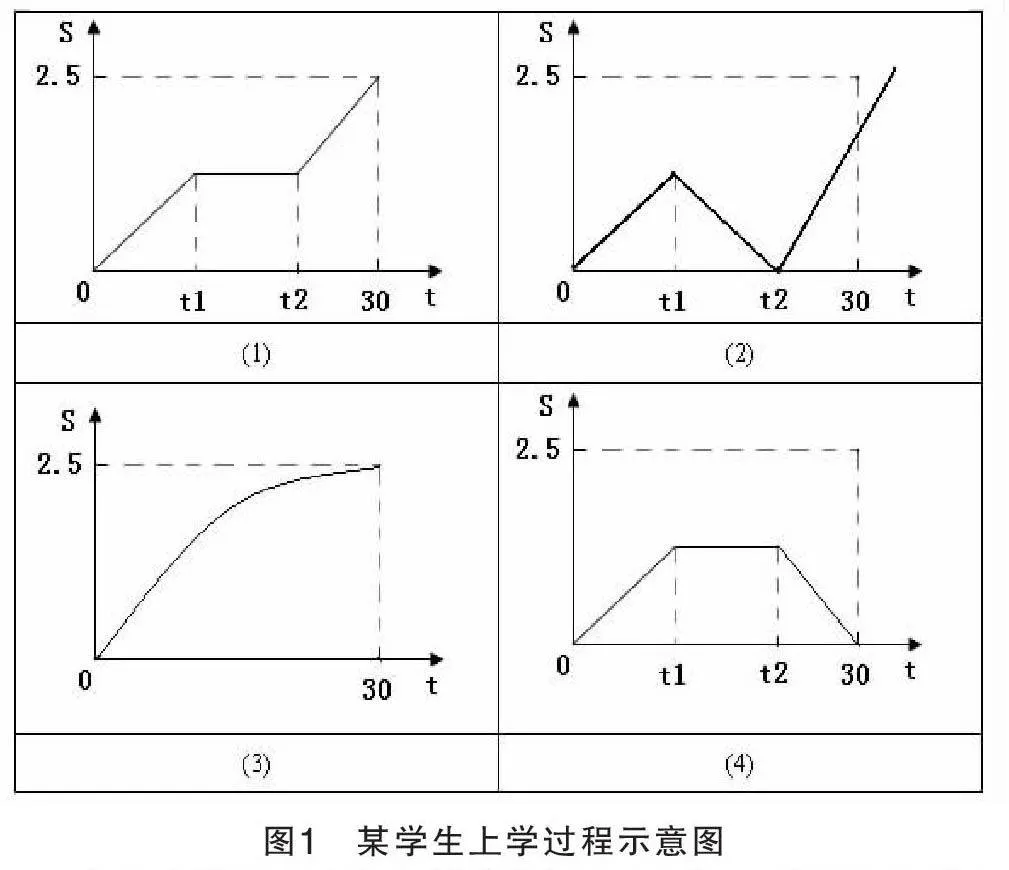
函數的基本思想是：通過某一事物的變化推知另一事物的變化，它的基本手段是：將變化事物的關系抽象化（如用公式法表示）、形象化（如用圖形法表示）、簡單化（如用表格法表示）。為了理解三種表達方法的聯系與區別及優缺點，可以用新產品定價和銷量的調查舉例：如果想了解新產品定價和銷量的關系，以便定價后決定生產多少產品，避免產品滯銷，則可以先用表格進行調查，即問受訪者，各種價格條件下，所愿意購買的數量，可以做成表格，即表格法；為了直觀形象，可以根據表格畫出散點圖，即圖形法；對圖形法中的散點圖去描繪一條穿過散點的直線，并用公式表示，則是公式法。還可以舉生活中的例子：某學生的家距離學校2.5公里，早晨7：30從家里騎自行車出發去上學，8：00上課。試問圖1中四個圖形和下述四件事相吻合，其中S表示離開家的距離，t表示時間。

（1）離開家后不久，自行車壞了，修好后再繼續騎車，準時到達學校。顯然和圖1之（1）對應。

（2）離開家后不久，發現忘記帶語文課本，立即回家取課本再去上學，結果遲到了。顯然和圖1之（2）對應。

（3）離家后想早點到學校便快速行駛，半路上遇到同學后邊聊天邊走，準時到達學校。顯然和圖1之（3）對應。

（4）離家后不久出了車禍，到附件醫院治療后打的回家。顯然和圖1之（4）對應。

從這個例子中可以看到圖形來源于表格，而圖形又可以表示成公式，即三者是等價的，只是表達形式不同而已。其中公式法最容易處理和運算，所以一般用公式法表達函數。公式法表達的函數有兩要素，為對應法則f和定義域D，即此兩要素可以決定函數。為了解釋定義域，可以用上面兩個例子，價格顯然不會低于0，而時間和距離也一般是正數。所以兩者的關系是有范圍的，或者說自變量的不同取值范圍和因變量的對應關系是可能變化的。這樣就引入了分段函數。分段函數在生活中隨處可見：寄包裹以本省外省、重量屬于什么范圍分類收費，居民用電的階梯電價，個人所得稅累進稅率，手機閑時和忙時分時段收費。可見這種函數關系是有范圍的，分段的，而不是放之四海而皆準的。函數可用于解決現實問題，往往來源于現實需求，而且解決方法也經常符合一般人的直覺，正如孔子說的“道不遠人”。只是數學形成一個邏輯體系，對我們的直覺證實或證偽而已，于是更為嚴謹、簡練、精確。當然，數學形式上更為抽象、深奧、晦澀。這樣啟發學生體驗到自己本身就有這樣的思維，而不是外在強行灌輸的知識，則能融入內心，發乎自覺，自然而然。這樣掌握的數學知識才能理解深刻、記憶牢靠、學以致用。

二、函數的基本性質

函數的兩要素可以決定函數，正如人可以用肉體和精神兩要素進行識別和區分一樣，根據兩要素識別人只是第一步，進一步可以了解其性格特征。函數具有四大性質：有界性、單調性、奇偶性、周期性。有界性可以使我們在考慮函數值變化時有一個參考范圍，即最大不過多少，最小不過多少；或者最好不過怎么樣，最差不過怎么樣。可以形象比喻為西游記中孫悟空就像函數那樣變化多端，但是無論如何翻筋斗云，都出不了如來佛的手掌，這就是界限，表示有界性。單調性可以表示變量間是否同方向變化，單調增表示同方向變化比如經濟學中的供給函數，圖形類似于走上坡路；單調減表示反方向變化，比如經濟學中的需求函數，圖形類似走下坡路。

奇偶性來源于自然界中很多事物呈現出各種各樣的對稱性，從人身體上的許多器官到建筑物的各種形狀，函數中的奇偶性是一個最基本的反映。關于y軸對稱的函數是偶函數，關于原點對稱的是奇函數。化學上諸多化合物分子如甲烷、苯的分子結構是對稱的。微生物中比如病毒的形狀多為對稱的，除流感病毒呈螺旋形外，其他如皰疹、牛痘、人體肉贅的病毒及腺病毒等皆為正20面體狀。在物理上，許多晶體的外形及內部構造也都是對稱的。用對稱思維可以發現自然界中的許多奧秘。科學家赫謝爾于1800年在紅光區域外側發現了紅外線后，人們根據對稱思維猜測在紫光區域外側也可能有一種看不見的射線。1801年，科學家里特果然在實驗室中發現了這種射線，即紫外線。

周期性是自然界中許多現象的共性，從一年四季春夏秋冬周而復始到鐘表指針轉動，從人們的呼吸和心臟跳動及心電圖到電流在導線中的傳播無一不在做周期性運動。周期性可以使我們由局部推知全局，由現在推知未來。正如《推背圖》中所言“一陰一陽，無終無始，終者自終，始者自始”，“茫茫天數此中求，世道興衰不自由，萬萬千千說不盡，不如推背去歸休”。19世紀，數學家約翰·傅里葉發現所有的樂聲（器樂和聲樂）都是周期正弦函數的和。在樂器的現代設計和聲控計算機的設計方面，周期函數是必不可少的。

三、反函數、復合函數、初等函數

在日常生活中，我們考慮問題有時候會從正反或者順逆兩方面考慮，比如新產品定價中要求價格做自變量，而需求量做因變量，即定價多少時候需求量是多少。如果有一批存貨，要求銷售出去，應該定什么價格的問題，就是逆過程。又比如溫度計中的水銀柱高度隨著溫度的不同而改變，即水銀柱高度h是溫度t的函數。而習慣上我們總是以相反的方式使用這個函數，即根據水銀柱的高度h確定溫度t，這時溫度t又成為高度h的函數。因此哪個變量是自變量，哪個變量是因變量要根據問題的性質和目的決定。這就必然要求提出反函數，而且反函數與原函數關于直線y=x對稱，具有對稱性。

生活中有許多連鎖反應，比如海洋中“大魚吃小魚，小魚吃蝦米”的現象，即表明大魚的數量是小魚數量的函數，而小魚的數量又是蝦米數量的函數；金屬棒子在加熱時，金屬棒的長度是溫度的函數，而溫度又是時間的函數，等等。這種連鎖反應現象的函數表達式，可以稱為函數的函數，即函數套函數，內層函數值作為外層函數的自變量，即為復合函數。復合函數還可以比喻為生產流水線，每個函數都可以看作為一道工序，可以把自變量看作輸入，因變量看作輸出，每道工序完成一種操作或者說功能，然后得到操作結果進入外層函數的下一道工序，一直進行下去，就得到成品了。初等函數首先要介紹六大類基本初等函數，然后由基本初等函數經過有限次四則運算和有限次復合運算得到的函數統稱為初等函數，因為初等函數有很多優良數學性質，比如后面要學的極限、連續性，所以微積分研究的主要對象就是初等函數。特別地，盡管分段函數的各段表達式一般是初等函數，分段函數是最常見的非初等函數。

參考文獻：

[1]張銀生，安建業.微積分[M].北京：中國人民大學出版社，2004.

[2]張祖錦.如何整體把握中職數學中的函數教學[J].課程教育研究，2012（20）.

[3]吳振奎，吳旻.數學中的美[M].上海：上海教育出版社，2004.