巧妙把握四項原則 激發學生學習動機

學習動機是學生掌握知識、形成高尚情操的重要因素，是發動、維持和引導學習活動的內部動力，是學習過程的核心。教師在備課、上課方面如何下功夫對學生來說只是一種外因，其內因是學生自己的學習動機。因此如何培養和激發學生正確的學習動機是數學教學中的一個重要課題，筆者結合教學實踐就此闡述四個原則。

一、直觀原則

教師在講授每一節課前，要讓學生清楚地了解這一節課的具體目標、任務和要求，這是調動學生積極性的有效途徑。在此過程中，最忌抽象說教，教師應盡可能用直觀形象的手段達到上述目標，讓學生一目了然。

二、創新原則

創新是課堂教學的靈魂。在教學過程中，新穎的教學內容、教學形式可以較好地激發學生的學習動機，提高學習興趣。

1.教學手段的創新。

教師應運用現代化的教學手段，將科學發現過程簡捷地重現于課堂，讓學生參與發現和創造的過程，指導學生動手、動腦，讓學生體驗作為學習主體進行探索發現和創造的樂趣。

如采取“引導發現法”教學“角平分線”一課，可這樣設計：（1）讓學生動手測量角平分線上的一點到角兩邊的距離。（2）利用多媒體演示，改變角平分線上的點的位置，改變角的大小，讓學生觀察分別在這兩種情況下該點到角兩邊的距離關系。（3）引導學生說出“角平分線上的點到角兩邊的距離相等”這個結論并證明。

2.教學形式的創新。

教學中如能抓住初中學生活潑、好動、好奇心強的特點，采取一些新穎的、靈活多樣的教學形式，必將激發起學生的積極性，提高其學習興趣。

教師可選擇一些適當的內容，事先布置給學生，讓學生充當“小老師”，由他們上講臺來講解，進行角色互換。在講完“平行四邊形的判定”后，筆者安排了一節習題課，讓學生做一次老師，許多學生躍躍欲試，課前精心準備，課上共有5位學生講解了5種證法。在這個過程中，學生在掌握知識的同時，能力也得到了鍛煉，學習主動性被激發，獲得了一次全新的體驗。

三、差異性原則

由于學生的學習水平和智力水平有較大的差異，教學中教師可進行分層教學，開展形式多樣的活動，使每一名學生都能體會到成功的快樂。

如在教學“等腰三角形的判定”時，我設計了這樣一組題目：

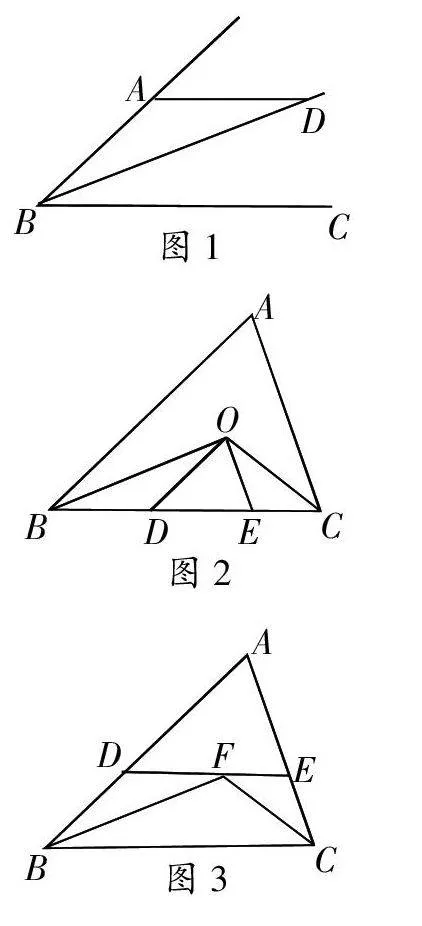
問題1 已知：如圖1，BD平分∠ABC，AD∥BC。求證：AB=AD。

問題2 已知：如圖2，BO、CO分別是∠ABC、∠ACB的角平分線，OD∥AB，OE∥AC，BC=10cm。求△ODE的周長。

問題3 已知：如圖3，∠ABC、∠ACB的角平分線相交于點F，過點D作DE∥BC，交AB于D，交AC于E。求證：BD+EC=DE。

問題4 已知：在上題中，若DF=EF，則圖中有哪些等腰三角形？為什么？

問題1是一個基本題，要求每一名學生掌握；問題2、3在基本題上有所提高，絕大部分學生通過努力可以解決；問題4留給學有余力的學生課外思考。

四、相關原則

在學生缺乏學習動力、沒有明確目標的情況下，教師可以利用學生對其他活動的興趣，從中找到與數學的“連接點”，通過引導，促使學生學習動機的轉變，從而使他們產生學習的意愿。

如針對班級中一些基礎差、對數學不感興趣的“足球迷”，在教學“一元二次方程的應用”時，筆者布置了這樣一道題目：在全國足球甲A聯賽前九輪比賽中，大連萬達隊保持不敗，共積得25分。按比賽規則，勝一場得3分，平一場得1分，問該隊共勝幾場球。這種新題，可使這些“足球迷”興趣盎然，沉浸于對題目的求解中，這樣通過突出“連接點”，可實現學生學習動機的轉移。

當然，培養和激發學生的學習動機，調動他們的積極性，非一朝一夕之事，在教學中，應遵循漸進原則。同時還應注意講授內容的適度、教師授課態度的示范、教師與學生感情的相容等原則。

（作者單位：江蘇省常熟市大義中學）