小內射環的擴張
沈 亮 陳建龍
(東南大學數學系,南京 210096)
設R為環,MR表示M為右R-模,EndMR表示MR的自同態環.f=c·(c∈R)表示f為通過R中元素c進行左乘的一個映射.J=J(R)表示環R的Jacobson根.
環R稱為右自內射環如果其作為右R-模為自內射模.這等價于每個從R的右理想到RR的同態,存在c∈R使得f=c·.類似可定義左自內射環.通過將環的理想限制在小理想上,Yousif和Zhou在文獻[1]中引入小內射環的定義.環R的右理想I是小理想當且僅當I包含在J(R)中[2].環R稱為右小內射環如果每個從R的小右理想I到RR的同態f可擴張為RR的一個自同態.類似可定義左小內射環.
文獻[1]中給出了環的小內射性與自內射性及相關自內射性的推廣之間的聯系.其中的一些主要結論在文獻 [3-4]中得到改進.本文將討論一些擴張環如環的平凡擴張、形式三角矩陣環、上三角矩陣環以及群環的小內射性.
1 一些定義
首先給出一些環的擴張的定義.
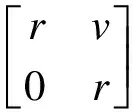
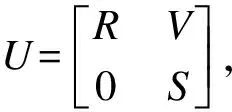
定義3設R為環,n≥1.Tn(R)表示R上的n階上三角矩陣環.可證明Tn(R)的Jacobson根即該環中對角線元素取自J(R)的所有矩陣的集合.

式中,cμ=∑aσbτ滿足στ=μ.
2 主要結論
設R為環,RVR為一個雙R-模.則R=EndVR如果對?f∈EndVR,存在元素c∈R使得f=c·.首先討論環的平凡擴張的小內射性.
引理1[5]設S=R∝V,其中R為環,RVR為一個雙R-模.則S為右自內射環當且僅當V作為右R-模為自內射模且R=EndVR.
有如下定理:
定理1設S=R∝V,其中R為環,RVR為一個雙R-模.下列性質等價:
1)S為右自內射環.
2)S為右小內射環.
3)V作為右R-模為自內射模且R=EndVR.
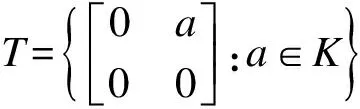
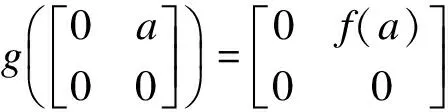
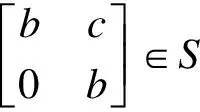
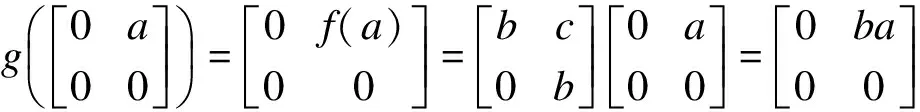
故f(a)=ba,?a∈K.所以f=b·.因此V作為右R-模為自內射模且R=EndVR.
由于環R作為R-模為雙模,且R=EndRR,則有如下推論:
推論1設R為環,S=R∝R.下列性質等價:
1)R為右自內射環.
2)S為右自內射環.
3)S為右小內射環.
注1在上述推論中,如果R為右小內射環,S未必為右小內射環.例如,令S=Z∝Z,其中Z為整數環.由于Z的Jacobson根為零,則Z為右小內射環,但S不是右小內射環.否則由上述推論得Z為右自內射環,但Z不是右自內射環.
接下來討論形式三角矩陣環的小內射性.
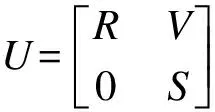
1)S為右小內射環.
2) HomS(K,S)=0.
3) 如果f∈HomS(K,V),則存在r∈R使得?k∈K,f(k)=rk.特別地,VS為自內射模.
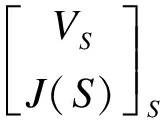
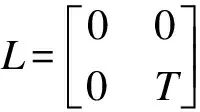
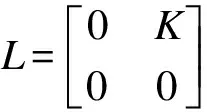
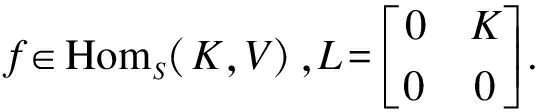
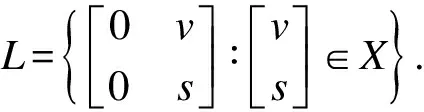
注2根據定理2中的結論2),如果VS非零且S是右S-模的上生成子,則U不是右小內射環.
下述命題說明非平凡的上三角矩陣環不是右小內射環.
命題1設R為環,n≥2.則S=Tn(R)不是右小內射環.
證明用eij表示S中的滿足第(i,j)位元素為1,其余位置元素為0的矩陣,1≤i≤j≤n.令 0≠x∈R,則K=e1nxR為S的一個小右理想.下面定義從K到S的映射γ使得γ(e1nxt)=ennxt,?t∈R.則γ為從小右理想K到SS的一個右S-模同態.如果S為右小內射環,則存在矩陣C∈S使得γ(e1nxt)=Ce1nxt,?t∈R.取t=1,則ennx=Ce1nx.得x=0,與假設矛盾.
注3根據上述命題,如果取n=2,則S=T2(R)同時也是一個非右小內射的形式三角矩陣環的例子.
下面給出一個右小內射的形式三角矩陣環的例子.
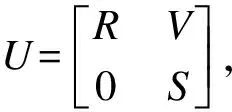
最后,給出關于群環小內射性的部分結論.環R稱為半局部環如果商環R/J為半單環.
引理2[6]設R為環,G為有限群.則群環RG為右自內射環當且僅當R為右自內射環.
引理3[7]設R為半局部環,G為有限群.則群環RG也為半局部環.
命題2設R為半局部環,G為有限群.下列性質等價:
1)R為右自內射環.
2)R為右小內射環.
3)RG為右自內射環.
4)RG為右小內射環.
證明根據引理2,1)?3)、1)?2)和3)?4)顯然成立.由于R為半局部環,G為有限群,由引理 3知,RG為半局部環.再由文獻[3]中引理3.13的結論(如果R為半局部環,則R為右小內射環當且僅當R為右自內射環)可得2)?1)和4)?3).
)
[1] Yousif M F, Zhou Y Q.FP-injective, simple-injective and quasi-Frobenius rings [J].CommAlgebra, 2004,32(6): 2273-2285.
[2] Anderson F W, Fuller K R.Ringsandcategoriesofmodules:graduatetextsinmathematics[M]. 2nd ed. New York: Springer-Verlag, 1992.
[3] Shen L, Chen J L. New characterizations of quasi-Frobenius rings [J].CommAlgebra, 2006,34(6): 2157-2165.
[4] Shen L.J-regular rings with injectivities [J].AlgebraColloq, 2013,20(2): 343-347.
[5] Faith C. Self-injective rings [J].ProcAmerMathSoc, 1979,77(2): 157-164.
[6] Connell I G. On the group rings [J].CanadianJMath, 1963,15: 650-685.
[7] Chin A Y M, Lumpur K. A note on semilocal group rings [J].CzechoslovakMathJ, 2012,52(127): 749-755.

