高超聲速內外流一體化飛行器動態特性

劉 緒，趙云飛，王東方，劉 偉

（國防科學技術大學 航天與材料工程學院，長沙410073）

高超聲速內外流一體化飛行器的動態穩定性參數（工程上常稱為“動導數”）研究是控制系統設計和動態品質分析的重要參數，其工程需求主要體現在以下3個方面［1］：①飛行器軌道設計的重要參數；②飛行器姿態控制系統設計的重要參數；③飛行器縱、橫向動態穩定性分析的重要依據。

隨著美國 HyperX［2］、FALCON（獵鷹）［3］和“黑雨燕”等項目以及在歐洲、日本等項目的相繼開展，吸氣式高超聲速飛行器的研究工作逐漸進入到工程預發展階段［4］。內外流一體化飛行器姿態控制精度要求很高以確保進氣道啟動，其操穩特性分析評估也更重要，需要準確預測動導數。X－51“乘波者”高超聲速飛行器第2次飛行試驗，由于超燃沖壓發動機的進氣道未能啟動而失敗。HTV－2首飛試驗失敗，在BTT（Bank to Turn）方式實現偏航過程中飛行器沿縱軸偏轉，在橫滾速度達到極限后超出可控范圍。美國工程審查委員會（ERB）分析認為：對飛行過程中的若干空氣動力學關鍵參數認識有限，在缺少主動控制的條件下，HTV－2將進入彈道螺旋飛行（典型的橫側不穩定問題）。

目前國內外對動導數辨識方面的工作主要還是針對傳統的以火箭發動機為動力的彈箭類飛行器，對包含內流的吸氣式飛行器動態特性研究較少。因此高超聲速內外流一體化飛行器的研制亟需開展動態特性模擬技術研究。其核心是三方向（俯仰／偏航／滾轉）的直接阻尼導數模擬方法研究；同時還迫切需要開展加速度導數、交叉導數、交叉耦合導數的數值算法研究，為縱橫向耦合運動特性研究提供技術支撐。動導數預測及穩定性預示將為飛行器控制系統設計、高超聲速飛行器動不穩定發生的邊界分析及相應的動態穩定性判據研究提供關鍵氣動參數。

動導數計算方法分為小擾動線化理論、牛頓理論與氣動力工程模型相結合的動導數工程近似方法、模擬動態實驗的數值自由振蕩法、數值強迫振蕩法。工程近似方法的最大特點在于快捷，但依賴于經驗性，考慮氣流分離、再附和尾流等效應較為困難，對于包含內流的一體化復雜外形流動難以適應。因此考慮了流動非線性的模擬動態實驗的全數值計算是動導數研究發展的重要方向。

本文在Etkin非定常氣動力模型基礎上，給出了小振幅強迫振動下的俯仰、偏航和滾轉三方向直接阻尼導數的強迫簡諧分析方法，并發展了包括交叉導數、交叉耦合導數在內的多種動導數辨識方法。在采用Finner標模驗證的基礎上，開展了高超聲速內外流一體化飛行器的動態特性分析。

1 數值方法

在貼體坐標系ξ－η－ζ下，對完全氣體、忽略質量

力下的三維無量綱Navier－Stokes方程形式如下：

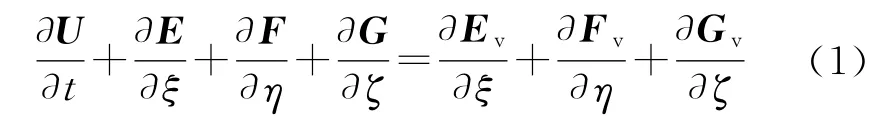
式中：U為守恒變量；E，F，G為無粘通量；Ev，Fv，Gv為粘性通量。

本文在空間上采用二階精度的Roe格式。Roe格式是基于Godunov方法的基本思路發展起來的，是通量差分分裂（FDS）格式的一種，由于其優秀的間斷分辨率和較小的數值耗散性，目前得到廣泛的應用。采用引入“雙時間步”（dual－time－step）方法的LU－SGS隱式格式離散流體運動方程時間項。動網格生成采用剛性網格生成方法。遠場入流邊界采用適用于動態邊界條件下的一維Riemann不變量的無反射邊界條件。對于定常／非定常超音速出流，邊界點上的值由內流場計算結果外推得到。對于壁面邊界，采用速度無滑移、絕熱壁條件。奇性軸采用外插后周向平均處理。

2 動導數計算方法

在飛行器姿態控制系統設計及軌道（彈道）設計中，所需要的動態穩定性參數有數十個之多。表1列出了一些重要的動態阻尼導數［5］。表中：Cl，Cm，Cn分別為滾轉、俯仰、偏航力矩系數；α，β分別為攻角和側滑角；p，q，r分別為滾動軸、俯仰軸、偏航軸的角速度分量。目前國內外公開文獻主要是研究俯仰、偏航或滾轉三方向的直接阻尼導數，而對交叉導數、交叉耦合導數的數值計算較少涉及。本文采用小振幅強迫簡諧分析法給出了多種導數的數值辨識方法。

表1 動態阻尼導數

飛行器做單自由度的俯仰運動，如果其質心速度不變，則確定運動的獨立狀態變量只有攻角α和俯仰角速度q。對俯仰力矩系數Cm，根據Etkin假定［6］，俯仰力矩系數可寫成：

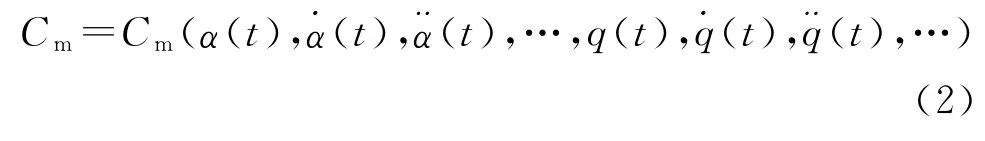
給定強迫振動：α（t）＝θ＝α0＋αmsinkt，其中，α為瞬時攻角，θ為俯仰角，α0為基準狀態的攻角，αm為攻角振幅，k為減縮頻率。在k不很大且忽略高階導數的影響時，當非定常振動過程達到諧振解，通過數值積分可以求出俯仰阻尼導數為

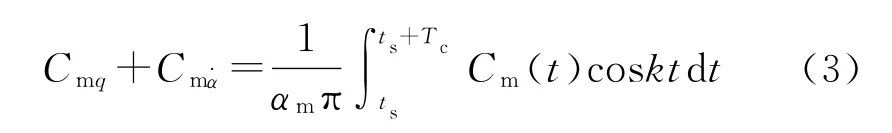
式中：ts為積分起始時間，Tc為振動周期。

類似地，通過給定不同的擾動方式可以推導出其他類型的動態穩定性參數的計算公式。其中強迫滾轉運動的形式為φ＝φmsinkt，φ為滾轉角，φm為滾轉角振幅；強迫偏航運動的形式為ψ＝ψmsinkt，ψ為偏航角，ψm為偏航角振幅。

3 驗證算例

本文采用Finner標模作為驗證算例，Finner標模是外形為“十”字翼的導彈，其動態特性有標準實驗數據和基于準定常歐拉方程的求解結果。圖1給出了“十”字翼導彈的外形尺寸［7］。導彈全長L為10倍的彈體直徑。本文采用塊間完全對接的多塊結構化網格，對稱面網格與分區情況見圖2。網格總量為200萬。近壁第一層網格到壁面的距離為1×10－4L。

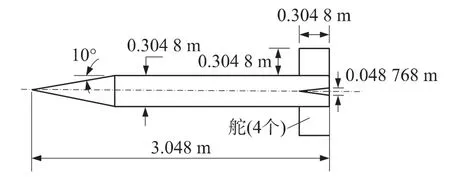
圖1 “十”字翼導彈外形尺寸

圖2 對稱面網格與分區圖

3.1 俯仰阻尼導數辨識

給定強迫俯仰振動形式α（t）＝θ＝α0＋αmsinkt，其中初始攻角α0＝1.5°，振幅αm＝1.5°，減縮頻率k＝0.05，質心位置Xcg／L＝0.5。

圖3給出了俯仰阻尼導數的計算結果與實驗數據［8］和基于準定常歐拉方程結果［9］的比較。從中可以看出，本文預測的俯仰阻尼導數比文獻中采用準定常歐拉方程的求解結果更加接近風洞實驗的數據。

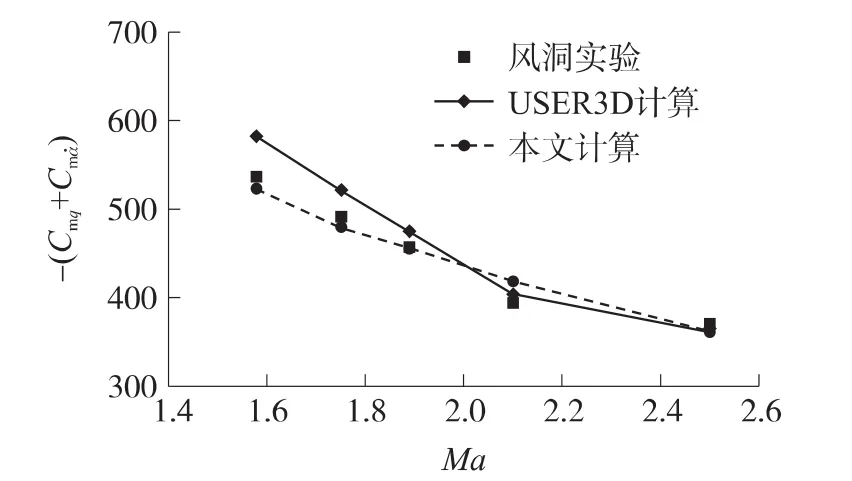
圖3 俯仰阻尼導數計算結果

3.2 滾轉阻尼導數辨識

給定強迫滾轉振動形式φ＝φmsinkt，取φm＝2.5°，k＝0.05，Xcg／L＝0.5。

圖4將強迫滾轉辨識出的動導數與文獻［10－11］中的實驗數據進行了比較。滾轉阻尼導數的實驗精度一般不高，主要由于實驗中存在支架、洞壁干擾等不確定因素，這使對同一模型在不同風洞中的實驗結果也存在一定的差異。本文計算得到的滾轉阻尼導數介于2個實驗結果之間，驗證了方法和程序的可靠性。

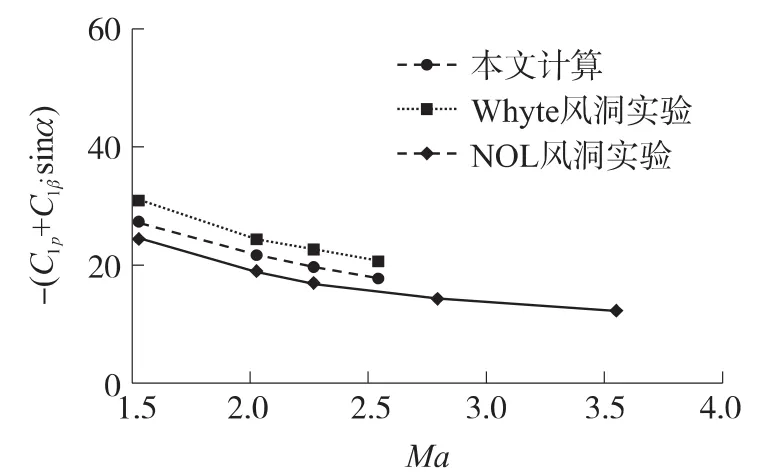
圖4 滾轉阻尼導數計算結果

4 動態特性分析

高超聲速巡航導彈X－51是美國空軍研究實驗室（AFRL）聯合波音公司（負責機身）和普惠公司（負責發動機）研制的一架超燃沖壓發動機驗證機－乘波器（SED－WR）飛行試驗平臺。本文以內外流一體化飛行器X－51為背景，利用公開的圖像數據資料進行反向建模，生成的類X－51三維實體外形見圖5，其進氣道內部結構見圖6。通過開展小振幅強迫簡諧運動的非定常流場數值模擬，對進氣道冷流狀態下的類X－51動態穩定性參數進行數值辨識。

圖5 類X－51三維實體外形

圖6 進氣道內部結構

4.1 直接阻尼導數辨識

計算采用塊間完全對接的多塊結構化網格，網格總量為460萬，共劃分為62塊。不同位置的結構化網格與拓撲結構見圖7和圖8。計算條件為：馬赫數6.5，高度27km。俯仰／偏航／滾轉3個方向的強迫簡諧運動的振幅均為1°，k＝0.1，無量綱時間步長Δt＝0.005。圖9給出了攻角為0°時的強迫俯仰振動一個周期內不同時刻的壓力等值線，其中ti＝ts＋（i－1）Tc／4，i＝1，2，3，4。頭部斜激波、膨脹波以及尾翼激波在圖中清楚地反映出來，內部流動已經建立。同時可以看出強迫振動的振幅很小導致各時刻流場狀態差別不大。在攻角0°～6°范圍之間本文給出了3個方向強迫振動的力矩系數曲線，如圖10～圖12所示，圖中，Cmm，Cml，Cmn分別為俯仰、滾轉、偏航力矩系數。

圖7 對稱面網格與分區圖

圖8 舵面附近的結構化網格

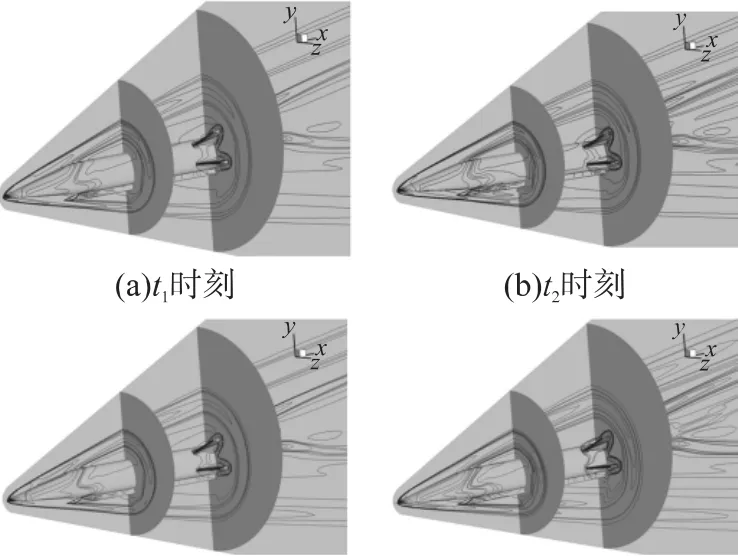
圖9 一個周期內不同時刻的壓力等值線

圖10 （a）、圖11（a）和圖12（a）分別給出了俯仰、滾轉和偏航運動對應力矩系數的遲滯環曲線。這是非定常運動時物體上漩渦運動和物面運動之間存在的時間延遲現象在氣動力系數上的反映。遲滯環形狀飽滿，非定常滯后效應比較明顯。在計算啟動后一個振蕩周期內即進入遲滯環，遲滯環重復性較好。不同攻角下的強迫振蕩遲滯環的轉動方式相互一致。從與3個遲滯環相對應的時間歷程曲線圖10（b）、圖11（c）和圖12（d）可以看到，非定常氣動力矩收斂情況很好，從第2個周期開始已經完全達到諧振。3個振動方向上的俯仰力矩系數、滾轉力矩系數、偏航力矩系數隨時間按正弦規律變化。

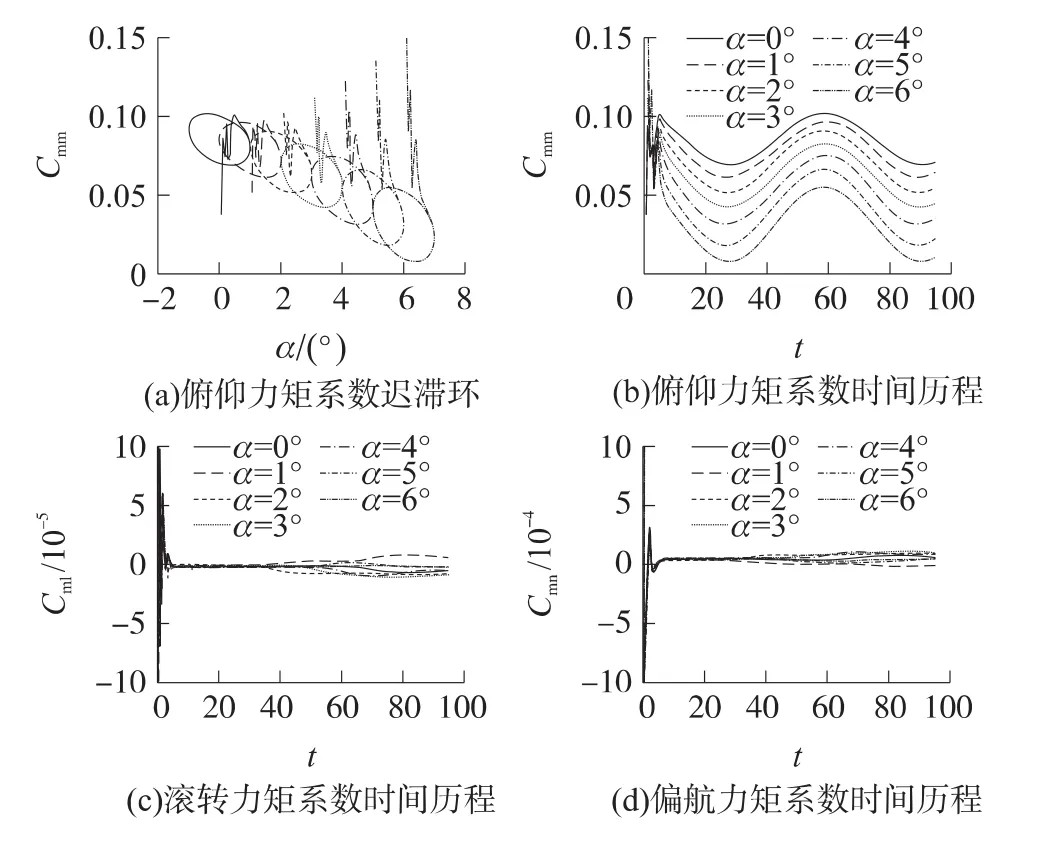
圖10 強迫俯仰振動力矩系數曲線

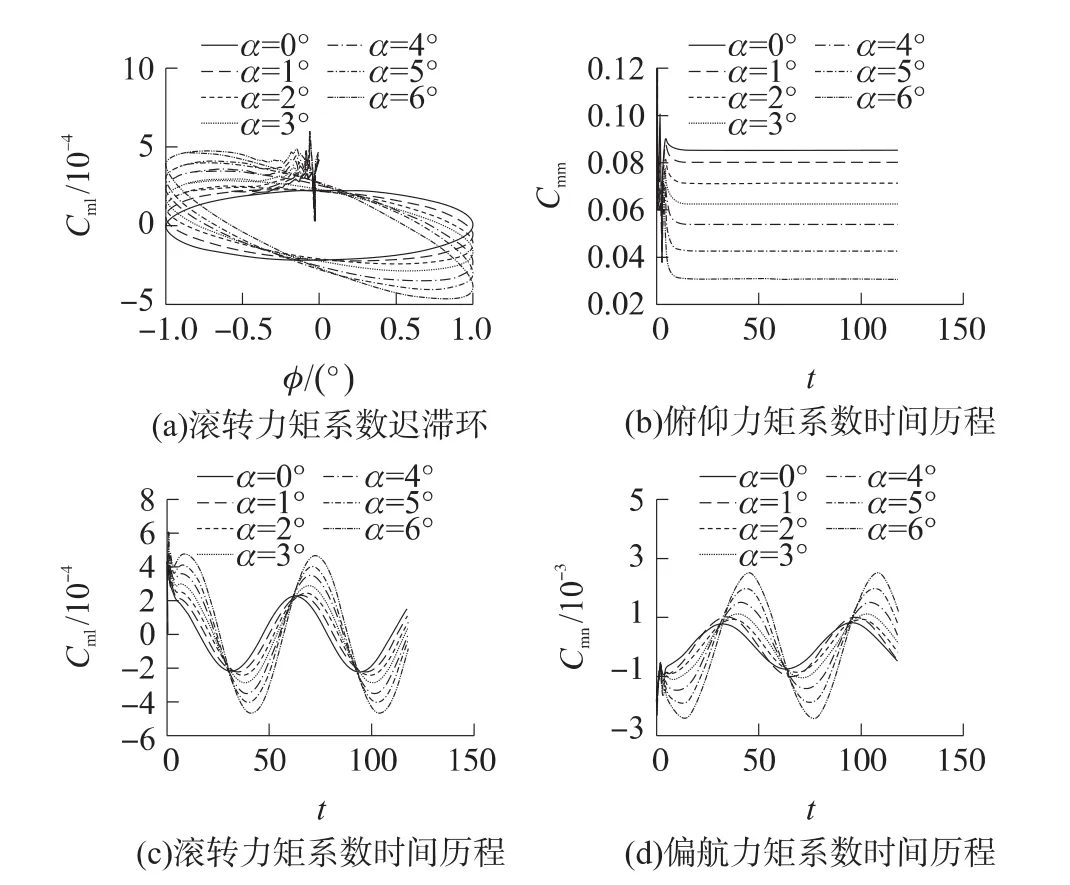
圖11 強迫滾轉振動力矩系數曲線

通過積分強迫簡諧振動的遲滯環曲線，表2給出了俯仰／偏航／滾轉3個方向的直接阻尼導數辨識結果。各方向下的直接阻尼導數均為負值，說明飛行器在俯仰／偏航／滾轉方向受到擾動后處于動穩定狀態。俯仰阻尼導數和偏航阻尼導數量級一致，但滾轉阻尼導數要小1～2個量級。

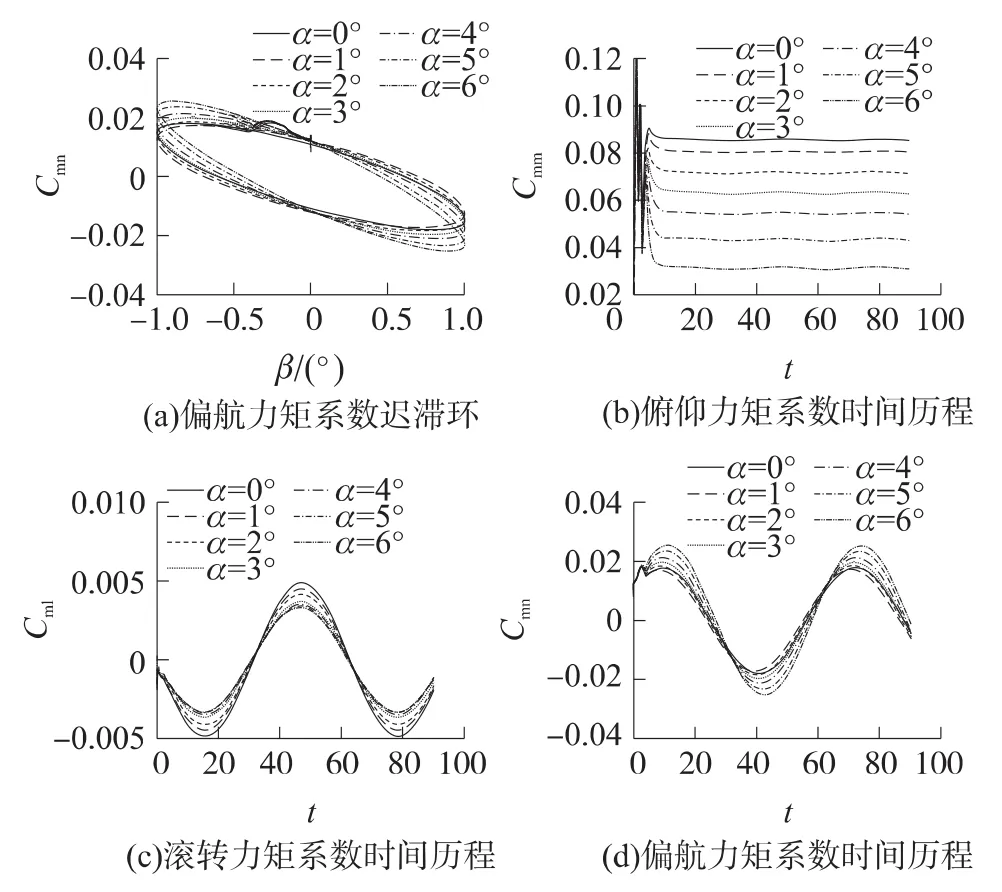
圖12 強迫偏航振動力矩系數曲線

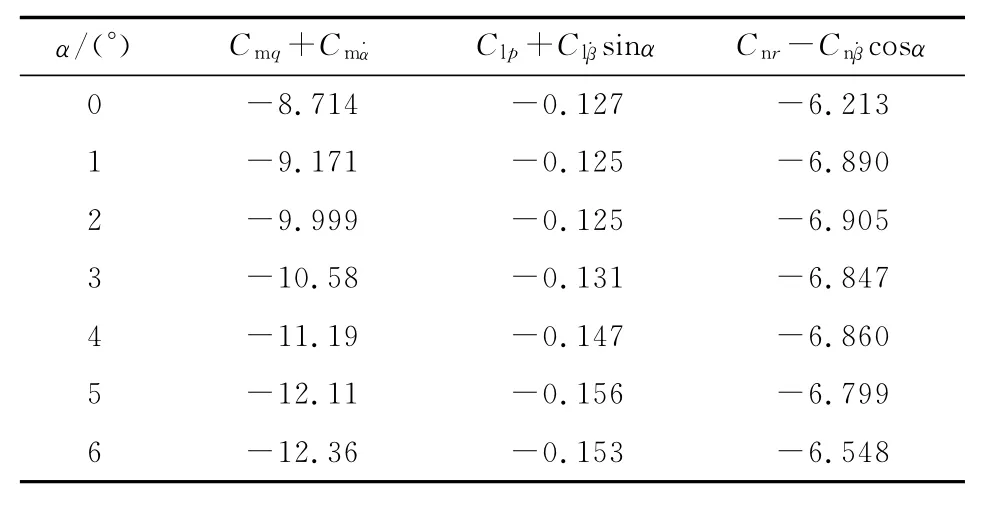
表2 直接阻尼導數辨識結果

4.2 交叉阻尼導數辨識

圖11（d）和圖12（c）的偏航和滾轉力矩系數隨時間變化能夠達到諧振，周期性變化明顯，說明滾轉方向和偏航方向的交叉性較強。但圖10（c）和圖11（b）中的力矩系數基本為一個常數，受周期性簡諧運動的影響不大，說明俯仰方向和滾轉方向的交叉耦合性很弱。類似地，圖10（d）和圖12（b）顯示出俯仰方向和偏航方向的交叉耦合性同樣很弱。綜合上述規律，在本狀態下飛行器偏航與滾轉橫向之間的影響明顯，但縱橫向交叉耦合性不強，故本文對交叉導數開展了數值辨識工作，其結果列于表3。

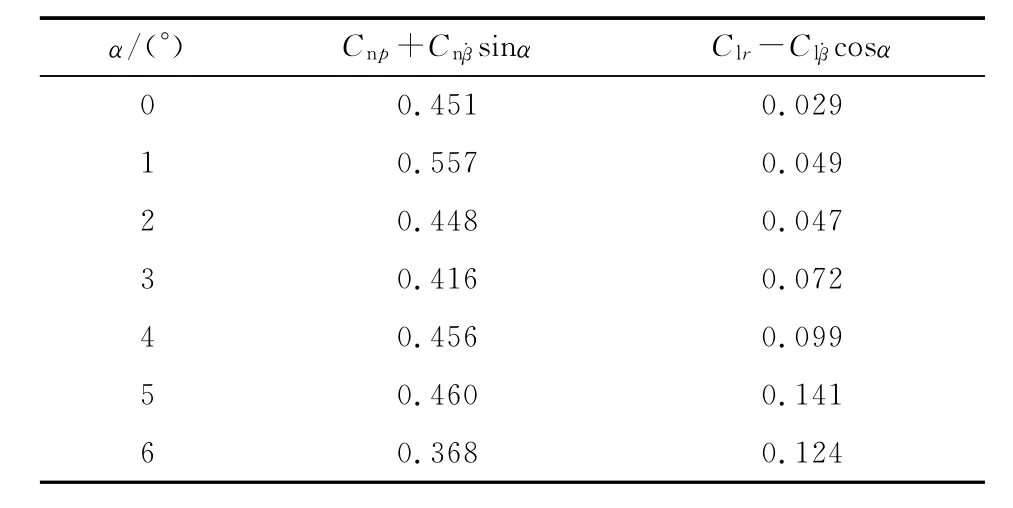
表3 交叉阻尼導數辨識結果

從辨識結果來看，強迫滾轉運動時滾轉阻尼導數在各計算狀態下均為負值，而滾轉－偏航力矩交叉導數均為正值，二者量級相差不大，說明飛行器在滾轉時是動穩定的，但可能引起偏航方向的動不穩定問題，需要控制系統對其姿態進行控制。強迫偏航運動與此類似，偏航阻尼導數在各計算狀態下均為負，而偏航－滾轉力矩交叉導數均為正，但其量級比偏航阻尼導數小2個量級。計算時涉及表面摩阻等復雜的計算問題，增加了計算難度，因此交叉導數的計算還需做深入研究。

4.3 強迫振蕩計算參數選取比較

強迫振動法辨識動態穩定性參數的精度依賴于3個重要的計算參數：時間步長、子迭代步數、減縮頻率。時間步長和子迭代步數這2個參數的組合實際上決定了雙時間步方法計算非定常流動的收斂程度。頻率相似問題是影響強迫振動法辨識動導數精度的重要影響因素。本文選取了幾組不同的參數值，分別考察時間步長、子迭代步數、減縮頻率對包含內流的高超聲速飛行器動導數辨識的影響。

減小時間步長、加大子迭代步數都可以提高非定常流動的收斂程度，從而提高動態穩定性參數的辨識精度，但計算量也會大幅增加。因此有必要先進行強迫振蕩的試算，確定保證準確度的適宜計算時間步長和子迭代步數。本文無量綱時間步長Δt取0.005，子迭代步數n為5步，在保證計算精度的前提下有較好的計算效率。表4給出了更小的時間步長和更大的子迭代步數時的動導數辨識結果，可以看到計算結果基本一致。

表4 不同時間步長和子迭代步數下的動導數辨識結果

減縮頻率實際上是強迫振動頻率快慢的反映，其大小會影響動導數的量值乃至符號。減縮頻率的選取必須像馬赫數、攻角一樣考慮到與實驗的相似性。本文以強迫滾轉運動為例，考察了不同減縮頻率對動導數辨識的影響。圖13顯示出遲滯環隨減縮頻率增加由內而外形成嵌套。減縮頻率越小，遲滯環曲線越狹長，非定常滯后效應越弱，動導數辨識難度高，非定常流場的計算量增大。但考慮到與實際情況的相似性，k不應取得過大，否則影響計算精度。表5給出了不同k值的滾轉阻尼導數和滾轉－偏航交叉導數，可以看出減縮頻率對動導數辨識結果的影響，隨著k的增大，橫向之間的影響加強。

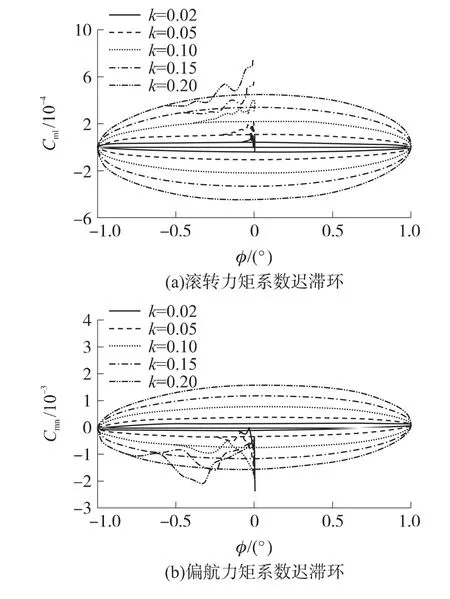
圖13 強迫滾轉振動不同減縮頻率下的遲滯環曲線

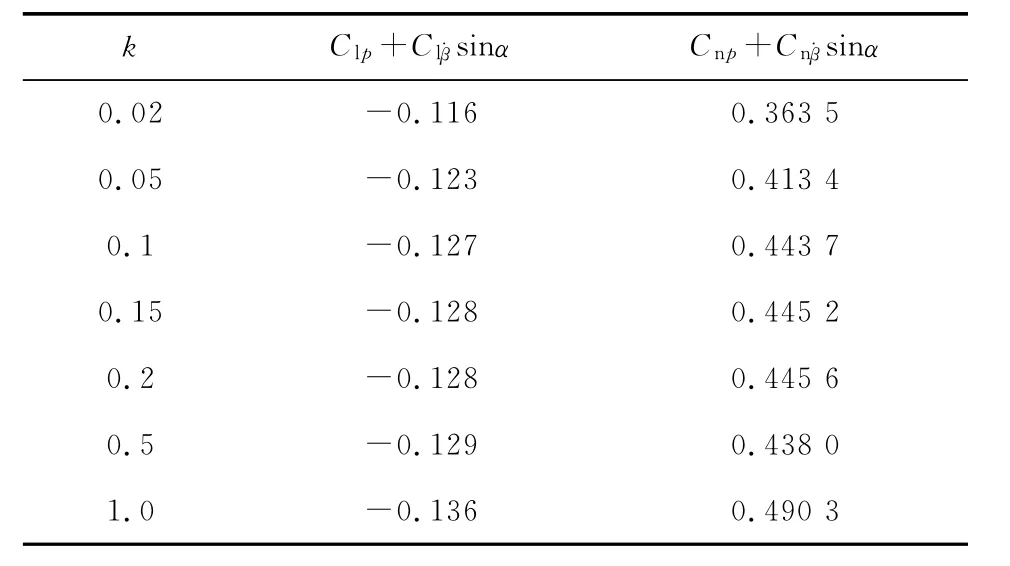
表5 不同減縮頻率下的動導數辨識結果

5 結論

本文基于三維非定常N－S方程，采用小振幅強迫簡諧分析法開展了高超聲速內外流一體化飛行器動態氣動參數的計算研究。本文給出的動導數辨識技術不僅適用于傳統的以火箭發動機為動力的彈箭類飛行器，對包含內流的吸氣式高超聲速飛行器適用性良好，各攻角下的非定常滯后效應明顯，遲滯環重復性較強。辨識得到的高超聲速飛行器3個方向的直接阻尼導數均為負值。對橫側向動穩定性、縱橫向耦合動穩定性問題的分析顯示，其縱橫向耦合性不強，但橫向之間的交叉影響明顯，各交叉導數均為正值，但可能引起偏航／滾轉方向的動不穩定問題，需要控制系統對其姿態進行控制。

［1］劉偉.細長機翼搖滾機理的非線性動力學分析及數值模擬方法研究［D］.長沙：國防科學技術大學，2004.LIU Wei.Nonlinear dynamics analysis for mechanism of slender wing rock and study of numerical simulation method［D］.Changsha：National University of Defense Technology，2004.（in Chinese）

［2］PEEBLES C.The X－43Aflight research program：lessons learned on the road to Mach 10［M］.Washington，D.C.：AIAA Inc.，2007.

［3］WALKER S，RODGERS F.Falcon hypersonic technology overview，AIAA－2005－3253［R］.2005.

［4］楊超，許赟，謝長川.高超聲速飛行器氣動彈性力學研究綜述［J］.航空學報，2010，31（1）：1－11.YANG Chao，XU Yun，XIE Chang－chuan.Review of studies on aeroelasticity of hypersonic vehicles［J］.Acta Aeronautica et Astronautica Sinica，2010，31（1）：1－11.（in Chinese）

［5］童秉綱，陳強.關于非定常空氣動力學［J］.力學進展，1983，13（4）：377－394.TONG Bing－gang，CHEN Qiang.Some remarks on unsteady aerodynamics［J］.Advances in Mechanics，1983，13（4）：377－394.（in Chinese）

［6］劉偉，楊小亮，趙云飛.高超聲速飛行器加速度導數數值模擬［J］.空氣動力學學報，2010，28（4）：426－429.LIU Wei，YANG Xiao－liang，ZHAO Yun－fei.Numerical simulation of acceleration derivative of hypersonic aircraft［J］.Acta Aerodynamica Sinica，2010，28（4）：426－429.（in Chinese）

［7］MIKHAIL A G.Roll damping for projectiles including wraparound，offset，and arbitrary number of fins［J］.Journal of Spacecraft and Rockets，1995，32（6）：929－937.

［8］SHANTZ I，GROVES R T.Dynamic and static stability measurements of the basic finner at supersonic speeds，NAVORD Report 4516［R］.1960.

［9］OKTAY E.CFD predictions of dynamic derivatives for missiles，AIAA 2002－0276［R］.2002.

［10］REGAN F J.Roll damping moment measurements for the basic finner at subsonic and supersonic speeds，NAVORD Report 6652［R］.1964.

［11］WHYTE R H.Spinner－a computer program for predicting the aerodynamic coefficients of spin stabilized projectiles，Genera1 Electric Class 2Reports［R］.1969.