一種改進的自適應滑模變結構導引律

高 峰，唐勝景，師 嬌，郭 杰

（1.北京理工大學 宇航學院飛行器動力學與控制教育部重點實驗室，北京100081；2.中國運載火箭技術研究院，北京100076）

現代戰場立體化的趨勢對武器系統多用途化的需求逐步提高。對于新一代反坦克導彈，不僅要求能夠摧毀地面裝甲目標，還要求其具備一定的低空防御能力，如打擊處于攻擊狀態的武裝直升機。

相比于主戰坦克、裝甲車等地面目標，空中目標的機動性更強；但另一方面，由于飛行的需要，空中目標的防護相對薄弱，只要命中目標，反坦克導彈常用的戰斗部足以對目標造成致命毀傷。一般反坦克導彈的飛行速度與可用過載均低于專用的防空導彈，因此需要根據導彈的具體情況，設計合適的導引律，使其在保證命中精度的同時能夠合理分配彈道的過載。

經典比例導引律是攻擊非機動目標的最優導引律，可以實現非機動目標視線角速度的零化，但在攻擊機動目標時其性能會急劇下降。為提高導彈對高機動目標的攔截能力，研究人員基于不同的出發點提出了一些高精度改進比例導引律［1－3］，雖然可以實現對機動目標的攻擊，但存在著所需導引信息過多，或者形式復雜等問題，且并不適用于速度較低的反坦克導彈。

滑模變結構控制對干擾和攝動具有某種完全自適應的優點［4］，而且滑動模態對攝動的不變性十分有益于控制系統的設計。另外，滑模變結構控制設計比較簡單，便于理解應用，因此在導引律尤其是攔截高機動目標導引律的研究中得到了廣泛的應用與發展［5－10］。

本文以零化彈目視線角速度為出發點，設計了一種自適應滑模變結構導引律，并根據實際研究中出現的具體問題，改進了變開關項的形式，并綜合應用飽和函數，削弱了變結構控制的抖振現象，最終形成一種改進自適應滑模變結構導引律。導引律可以滿足反坦克導彈對空中目標的命中精度需求，同時可以合理分配末制導段的法向過載。

1 彈目相對運動關系

在縱向平面內，導彈與目標的相對運動關系示意圖如圖1所示。圖中，r為導彈相對目標的距離，vM為導彈速度，θM為導彈彈道傾角，q為彈目視線角，vT為目標速度，θT為目標航跡角。規定水平基準線逆時針旋轉到彈目視線上時，q為正，反之為負。

根據圖1所示的運動關系，得到彈目相對運動關系方程組：

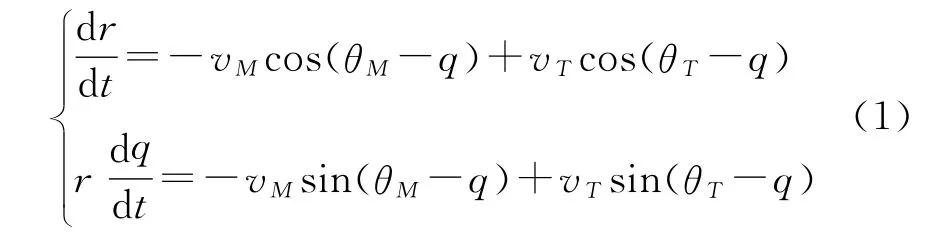
2 導引律初步設計與分析

2.1 導引律推導

對式（1）第二式求微分，并根據第一式進行簡化，可得：

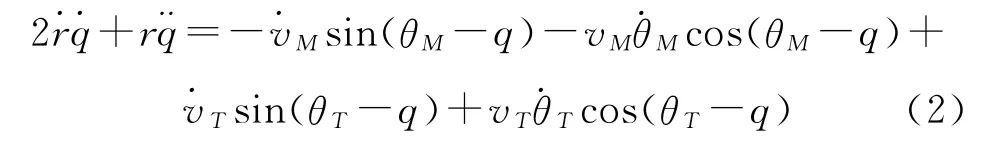
取u＝為控制項，由式（2）可得：

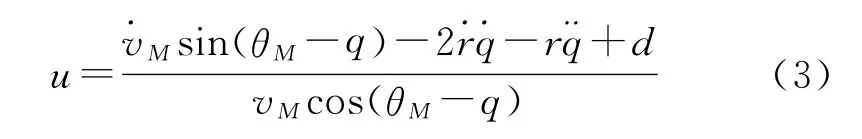
在導引律的設計中，根據準平行接近原理，一般希望在制導過程中使視線角速度趨近于0，即使導彈在目標機動時也可以實現的零化。為達到這個目的，應用滑模變結構理論，選取＝0作為導引律的切換平面，即切換函數設計為

通過變結構控制，使系統在有限時間內到達切換平面內，系統進入滑動模態時，即可使在有限時間內零化，滿足＝0的理想導引要求，在滑動模態附近，漸進實現平行接近導引。

為使系統到達切換面，要求系統的運動必須趨向切換平面，即滿足可達性條件：

可達性條件保證了系統運動可以在有限時間內到達切換平面，但對這段時間內具體的狀態軌跡沒有約束。為改善這段運動的動態品質，可以通過趨近率的設計加以控制。在滑模變結構導引律的研究中，常采用指數趨近率的形式。根據導彈控制系統的時變性，設計一種對時變參數具有自適應能力的指數趨近率，具體形式為

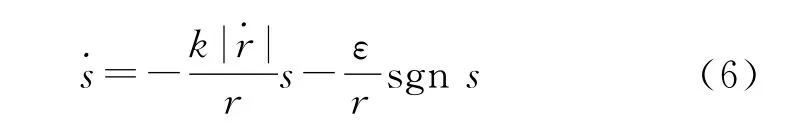
式中：k＞0，ε＞0。

趨近率表達式（6）的自適應性主要體現在切換函數向切換面的運動速率隨彈目距離r的變化而調整。在末制導初始階段，r較大，趨近速率較慢；隨著導彈接近目標，r→0時，趨近速率迅速上升，保證了不會發散，從而提高了命中精度。在式中，當s＝→0時，趨近速率約等于ε／r，可以保證有限時間到達切換面。由于趨近率的自適應性，最終得到的導引律也具有了自適應能力。

將式（4）、式（6）代入式（3），求得控制項：

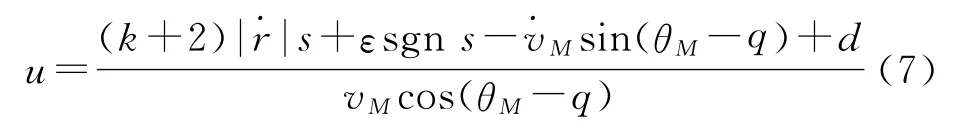
在實際制導過程中，目標的機動信息一般很難準確獲取，通常利用卡爾曼濾波或擴展卡爾曼濾波技術，通過建立目標機動模型，可以實現目標的加速度估計。但這種假設的目標機動模型在工程上可能存在很大的建模誤差，甚至導致糟糕的估計結果。因此，在滑模變結構導引律的研究中，可以將其作為干擾項處理［11］。

將d作為干擾項進行簡化后，式（7）可簡化為

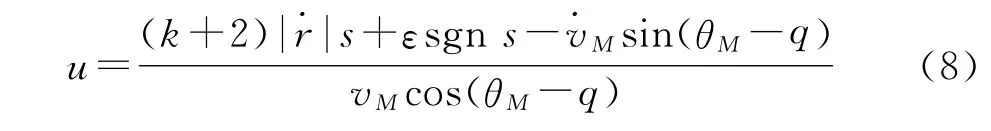
從而可以得到自適應滑模變結構導引律的形式：

2.2 穩定性分析

構造Lyapunov函數：

根據式（3）以及式（8），可得Lyapunov函數的導數：

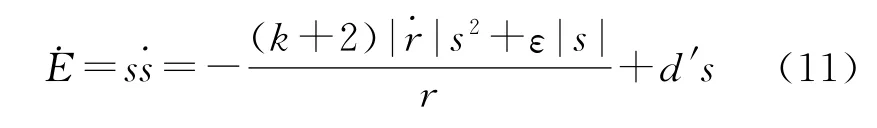
式中：d′為目標機動干擾項的預估值，可根據目標特性離線估計。

根據Lyapunov穩定定理，為使導引律收斂，需要有＜0。因此，根據式（11），需要滿足：

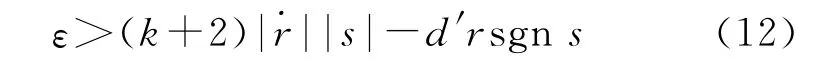
則可保證系統漸進穩定。

2.3 導引律分析

如式（9）所示，設計的自適應滑模變結構導引律可視為由比例導引項、切換偏置項以及加速度補償項等3部分組成。反坦克導彈在末制導段一般進行無動力飛行，切向加速度較小，若忽略導彈攻擊段的切向加速度，則式（9）可簡化為

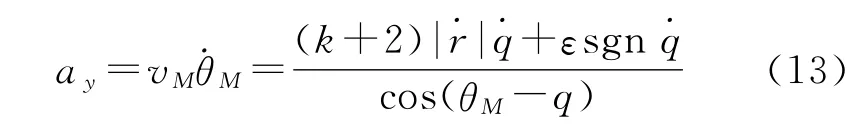
即導引律可視為一種具有時變比例系數和一個切換偏置項的改進比例導引律。該導引律無需估計目標機動信息，僅需目標機動的界限即可。滑模條件滿足時，控制指令中的切換偏置項起到了估計目標加速度的作用。

3 導引律的改進

3.1 抖振的削弱

對于采用滑模變結構控制的系統，在實際控制過程中，開關在時間和空間上的滯后會導致控制的不連續性，產生抖振現象，進而影響控制系統的穩定性，導致導彈命中精度的降低。抖振是變結構控制系統的嚴重缺陷，也是阻礙變結構控制應用的主要障礙［12］。在導引律的研究中，為削弱抖振現象的影響，目前最常用的方法是飽和函數法，另外還有變開關項系數法等。

1）飽和函數法。

飽和函數法的基本思想是將不連續的符號函數連續化，具體可將符號函數取代為

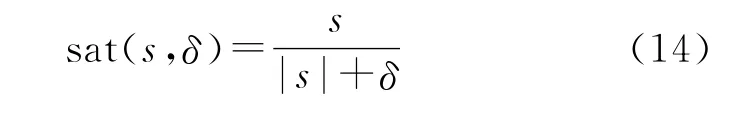
或

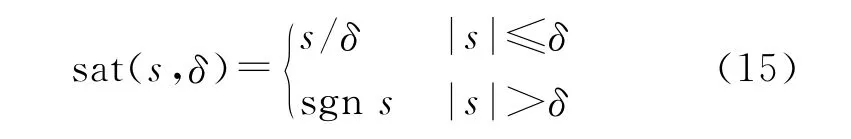
式中：δ＞0，是一個微小量，一般可稱為邊界層厚度，也稱為消顫因子［13］。

以改進后的函數代替符號函數，可使控制在切換面附近具有高增益性。若δ較小，則可保持高度的魯棒性；但實際在控制器上，大幅時間滯后需要較大的δ，且在極端情況下，將導致大幅振動且系統不再是變結構系統。

在飽和函數法的2種形式中，式（14）抑制抖振的效果更好，因此也更為常用。另外還有一種死區法，可視作飽和函數法的一種變形，因其抑制抖振的效果不如飽和函數法，所以并不常用。

2）變開關項系數法。

變開關項系數法可以視作趨近率參數調節方式的一種改進，趨近率表達式中含有符號函數的εsgn稱為開關項，系數ε的取值非常關鍵。根據式（6），若ε選擇較小的值，狀態軌跡接近切換面時的運動速率變小，可有效減小顫振幅度。但若ε選擇過小，會導致到達切換面的時間無窮大，系統不再是滑動模態控制系統。

因此，為兼顧減少到達切換面的時間以及控制抖振幅度的目的，可設定ε為變量，隨著接近切換面，使ε逐漸減小。在文獻［14］中，劉永善等人研究了基于模糊控制技術確定ε變化的形式，可有效削弱抖振。但該方法需要應用彈上傳感器等設備對目標的運動進行預估，并且模糊器的設計也為導引律的設計增加了難度。

為此，本文采用變開關項系數法時，對ε的形式進行了改進，將ε設計為隨r逐漸減小的變量，即隨著導彈飛向目標，ε也隨之減小。為簡單起見，ε的形式設計為r的一次函數，即

式中：a＞0，b＞0，其取值需要根據ε的取值范圍及r的變化范圍進行。在接近目標時，r逐漸接近于零，因此可首先確定b的取值，其作用是保證系統在末制導的大部分時間內處于滑模控制系統；然后根據末制導開始時r的最大值和ε的上限進行a的取值，在保證系統可以較快進入滑模面的同時盡量減小抖振幅度。根據趨近率表達式中ε的作用可知，a和b的取值越大，系統進入滑模面的速度越快，同時出現抖振的可能性或抖振幅度也會增大。

3.2 導引律的改進

研究中發現，分別采用飽和函數或變開關項系數進行抖振的削弱處理，難以有效地削弱抖振現象。

如圖2～圖3所示，分別采用飽和函數法和變開關項系數法時，雖然末制導段的彈目視線角速度進入滑模面的速度較快，但均出現了不同程度的抖振現象。其中，采用變開關項系數法時，盡管對的抑制效果更好，但抖振現象也更為嚴重。而且飽和函數中消顫因子δ取值越小，或是變開關項系數中參數a和b的取值越大，抖振現象越嚴重；反之，對的抑制效果會下降，當抖振現象完全消除時，甚至無法進入滑模面。

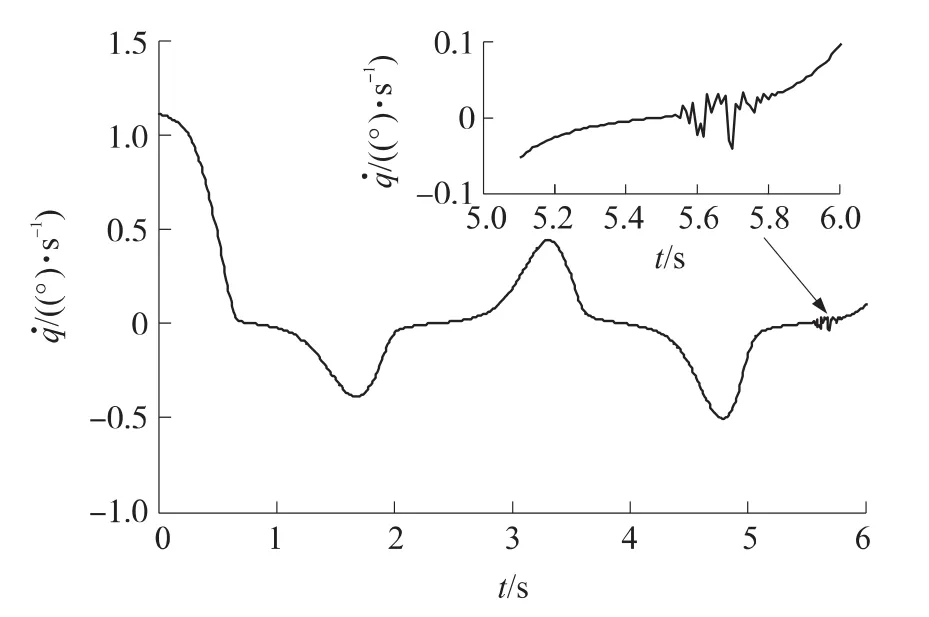
圖2 采用飽和函數法時的彈目視線角速度曲線

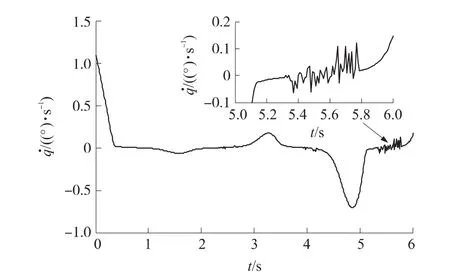
圖3 采用變開關項系數法時的彈目視線角速度曲線

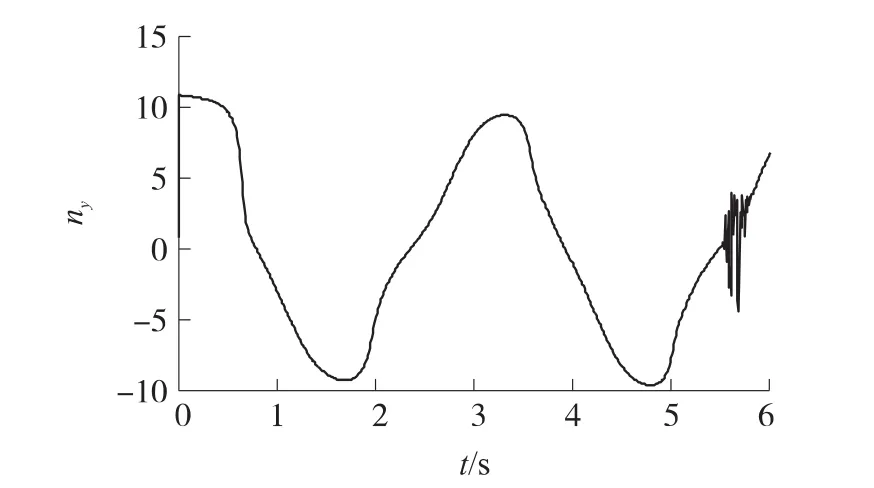
圖4 采用飽和函數法時的法向過載曲線

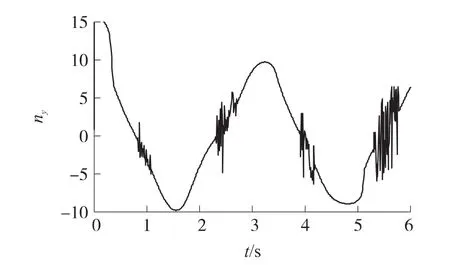
圖5 采用變開關項系數法時的法向過載曲線

在本文研究中，嘗試綜合采用飽和函數法和變開關項系數法進行消顫處理，取得了較好的效果。首先，用飽和函數替換導引律表達式中的符號函數，然后采用本文設計的一次函數形式的變開關項系數，將式（14）和式（16）代入式（9），最終得到改進的自適應滑模變結構導引律：

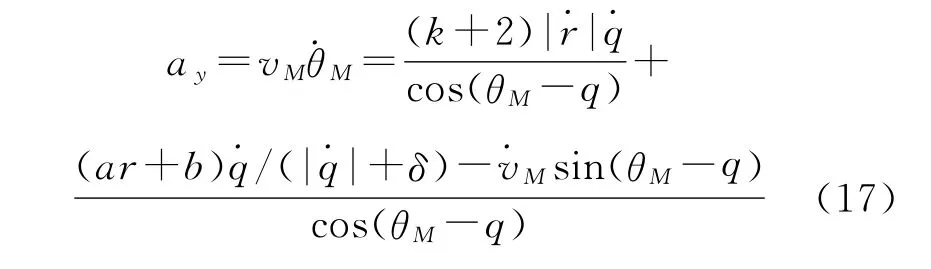
若忽略導彈攻擊段加速度，則式（17）可變為

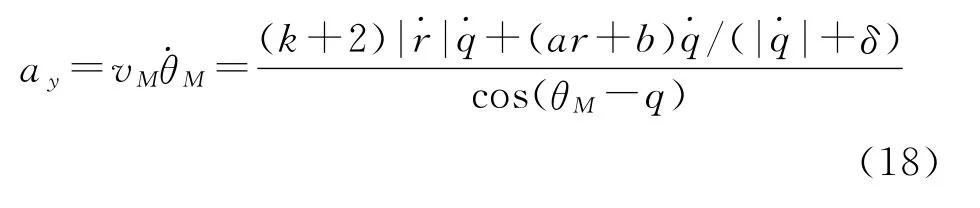
4 仿真分析

基于導引彈道仿真對設計的導引律進行仿真分析，仿真參數設置如下：導彈平飛高度h＝150m，速度為vM＝180m／s；目標初始位置（2 000，300）（m）；轉入末制導時刻彈目水平距離rx＝1 000m，并以此時刻作為仿真開始時間，即t＝0；同一時刻目標開始作蛇形機動，目標運動參數為vT＝50m／s＝10g（cos2t）／vTs－1；導引頭盲區距離為70 m，導彈進入盲區時給予視線角速度信號零值，以此為依據計算脫靶量。仿真中比例導引律（PNG）的比例系數取4；改進自適應滑模變結構導引律（IAVSG）中的參數取值為k＝2，δ＝0.001，a＝0.1，b＝50。仿真得到彈道曲線以及各類參數變化曲線如圖6～圖9所示。

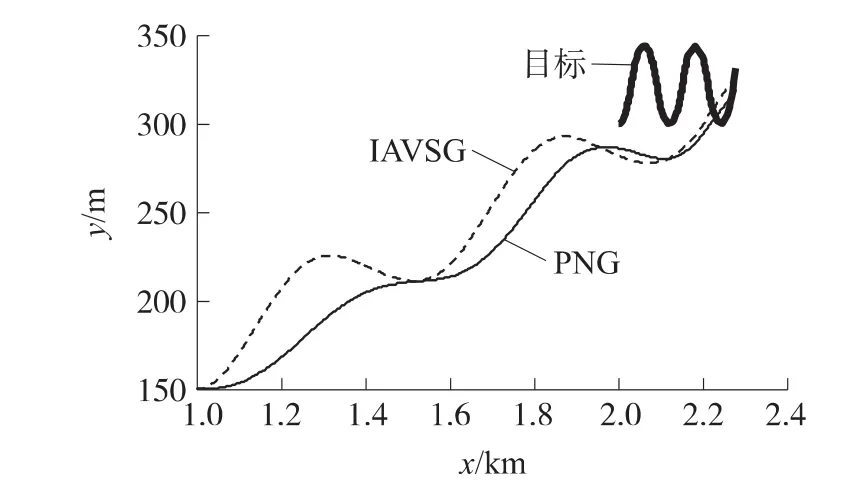
圖6 彈道曲線比較

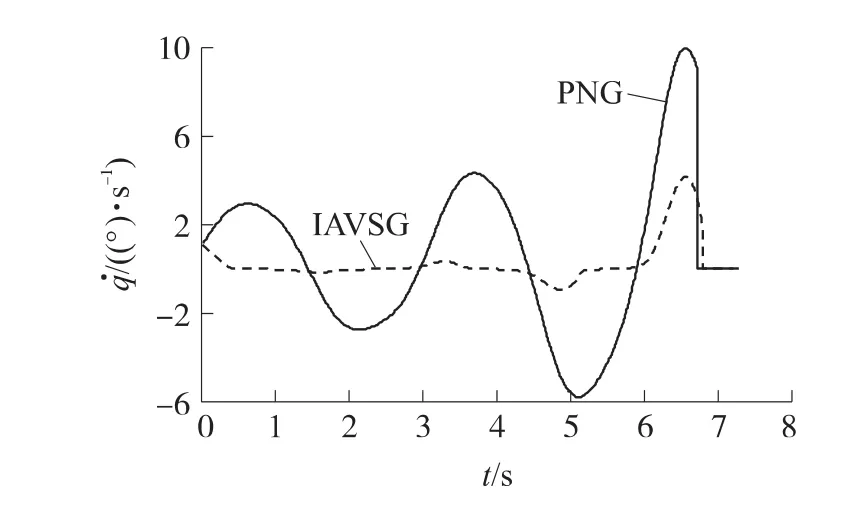
圖7 彈目視線角速度曲線比較

圖8 法向過載曲線比較

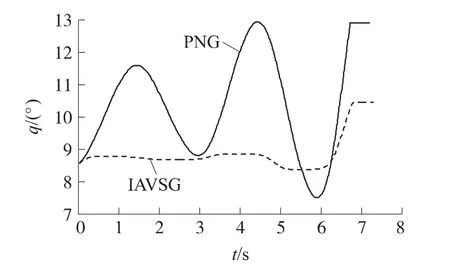
圖9 彈目視線角曲線比較

如圖6所示，IAVSG的彈道曲線機動幅度比PNG大，而且距目標越遠時這種對比越明顯，說明IAVSG為抑制的變化在末制導開始階段導彈就需要隨目標的機動進行較大幅度的機動。

如圖7所示，在末制導開始后，采用IAVSG的很快進入滑模面，在最后階段由于彈目距離過小才離開了滑模面。與圖2、圖3相比，進入滑模面的速度較快，雖然對的抑制效果稍差，卻完全消除了的抖振現象。而采用PNG時變化很大，尤其在接近目標時甚至接近10（°）／s。

抑制的代價就是在追擊過程中一直需要導彈進行較大幅度的機動，因此法向過載會保持在較大的范圍內變化，如圖8所示。但在接近目標時，IAVSG的法向過載要小于PNG，因此可以視為IAVSG可以更合理地分配整個末制導段的法向過載。與圖4、圖5相比，采用IAVSG的法向過載曲線也完全消除了振蕩現象。

圖9所示為彈目視線角q的變化曲線，由于受到了抑制，因此采用IAVSG時q的變化明顯要比采用PNG時小很多。

仿真得到PNG和IAVSG的脫靶量分別為2.473m和0.449m，說明在攻擊機動目標時IAVSG的精度要遠高于PNG。同時IAVSG也完全消除了變結構控制導致的抖振現象，有益于保持控制系統的穩定性。

5 結束語

本文提出的改進自適應滑模變結構導引律通過設計形式簡單的變開關項系數并綜合采用飽和函數法，兼顧了保證系統趨近速率和控制抖振的需求。該導引律具備了遠優于比例導引律的精度，并實現了對末制導段導彈法向過載較為合理的分配，可以滿足反坦克導彈對低空目標的作戰需求。同時本文提出的變開關項系數的形式及消除抖振的方法對變結構導引律的研究也有一定的參考價值。

［1］程鳳舟，陳士櫓.攔截彈頭的修正比例導引律［J］.空軍工程大學學報，2003，4（4）：15－18.CHENG Feng－zhou，CHEN Shi－lu.An amendable proportional navigation law for intercepting warhead［J］.Journal of Air Force Engineering University，2003，4 （4）：15 － 18.（in Chinese）

［2］郭鵬飛，任章.一種攻擊大機動目標的組合導引律［J］.宇航學報，2005，26（1）：104－106，111.GUO Peng－fei，REN Zhang.An integrated guidance law for target escapes with high acceleration［J］.Journal of Astronautics，2005，26（1）：104－106，111.（in Chinese）

［3］王輝，章虹虹.高精度偏置比例導引末制導律研究［J］.航天控制，2009，27（6）：19－22，32.WANG Hui，ZHANG Hong－hong.The development of highprecision biased proportional navigation terminal guidance control［J］.Aerospace Control，2009，27（6）：19－22，32.（in Chinese）

［4］HUNG Y W，GAN H J C.Variable structure control a survey［J］.IEEE Transactions on Industrial Electronics，1993，40（1）：2－22.

［5］BRIERLEY S D，LONGCHAM R.Application of sliding node control to air－air interception problem［J］.IEEE Transactions on Aerospace and Electronic Systems，1990，26（2）：306－325.

［6］RAVINDRA B K，SARMA I G，SWAMY K N.Switch bias proportional navigation for homing guidance against highly maneuvering targets［J］.Journal of Guidance，Control and Dynamics，1994，17（6）：1 357－1 363.

［7］ZHOU Di，MU Chun－di，XU Wen－li.Adaptive sliding－mode guidance of a homing missile［J］.Journal of Guidance，Control，and Dynamics，1999，22（4）：589－594.

［8］郭建國，周鳳岐，周軍.基于零脫靶量設計的變結構末制導律［J］.宇航學報，2005，26（2）：152－155，216.GUO Jian－guo，ZHOU Feng－qi，ZHOU Jun.Variable structure terminal guidance law based on zero miss－distance［J］.Journal of Astronautics，2005，26（2）：152－155，216.（in Chinese）

［9］楊軍.紅外尋的制導空空導彈變結構比例導引律研究［J］.西北工業大學學報，1998，16（1）：38－41.YANG Jun.A variable structure PN law suitable for high performance IR homing air to air missile［J］.Journal of Northwestern Polytechnical University，1998，16（1）：38－41.（in Chinese）

［10］宋建梅，張天橋.帶末端落角約束的變結構導引律［J］.彈道學報，2001，13（1）：16－19.SONG Jian－mei，ZHANG Tian－qiao.The passive homing missile’s variable structure proportional navigation with terminal impact angular constraint［J］.Journal of Ballistics，2001，13（1）：16－19.（in Chinese）

［11］任義元，袁建平，方群.空空導彈變結構末制導律研究［J］.計算機仿真，2009，26（10）：25－29.REN Yi－yuan，YUAN Jian－ping，FANG Qun.A study of terminal variable structure guidance law of air－to－air missile［J］.Computer Simulation，2009，26（10）：25－29.（in Chinese）

［12］顧文錦，趙紅超，楊智勇.變結構控制在導彈制導中的應用綜述［J］.飛行力學，2005，23（1）：1－4.GU Wen－jin，ZHAO Hong－chao，YANG Zhi－yong.Application of variable structure control in missiles guidance［J］.Flight Dynamics，2005，23（1）：1－4.（in Chinese）

［13］佘文學，周軍，周鳳岐.一種考慮自動駕駛儀動態特性的自適應變結構制導律［J］.宇航學報，2003，24（3）：245－249.SHE Wen－xue，ZHOU Jun，ZHOU Feng－qi.An adaptive structure guidance law considering missile’s dynamics of autopilot［J］.Journal of Astronautics，2003，24（3）：245－249.（in Chinese）

［14］劉永善，劉藻珍，李蘭忖.攻擊機動目標的被動尋的模糊變結構 制 導 律 研 究 ［J］.系 統 工 程 與 電 子 技 術，2007，29（2）：254－258.LIU Yong－shan，LIU Zao－zhen，LI Lan－cun.Research on fuzzy variable structure guidance law for passive homing missiles against maneuvering targets［J］.Systems Engineering and Electronics，2007，29（2）：254－258.（in Chinese）