中繼網絡中基于能量效率的動態用戶接入算法

李 欣 王 浩 孟 超 劉 楠 尤肖虎

(東南大學移動通信國家重點實驗室,南京 210096)

中繼網絡中如何合理配置網絡資源、提高網絡的能量效率是當前通信領域的一個研究熱點[1].Madan等[2]討論了基于最小化系統射頻和信道狀態信息量化能耗準則的用戶協作中繼選擇問題. Zhou等[3]提出了一種基于最小化每包能耗和最大化網絡生存時間的最優中繼選擇機制.在負載較輕時,小區基站本身就可以為用戶提供足夠的網絡資源,以保障所有用戶的通信質量,此時從提高能量效率的角度考慮中繼是否應該關閉是值得探索的問題[4].Marsan等[5]提出了一種同構網絡中基于時變負載模型的靜態站點休眠模型,該模型基于時變負載模型的特性,動態調整站點的休眠和工作狀態,以達到節省站點電路能耗、提高能量效率的目的.Gong等[6]進一步利用時變負載模型的特性,將站點休眠問題建模為一個動態優化問題,并提出了一種基于能量效率最優的站點休眠算法.然而,文獻[2-6]僅從部分系統能量效率的角度研究了中繼網絡的能量效率問題,沒有全面考慮系統能量效率,得出的結論很可能是片面且不準確的.

在中繼網絡的能量效率問題中,應綜合考慮系統中電路端和射頻端的能量效率.Zhou等[7]研究了一維中繼網絡中基于系統能量效率的中繼部署和中繼休眠概率的聯合優化問題;雖然綜合考慮了網絡中電路端和射頻端的能量效率,但該模型只能反映中繼位置固定場景下中繼的休眠概率,不能得到特定場景下中繼工作狀態的最優解. Li等[8]研究了中繼網絡中基于能耗最小的用戶接入方法.

本文從最大化系統能量效率的角度,研究了在負載受限并保證用戶速率要求前提下中繼網絡中的用戶接入問題.首先,將該問題建模為一個整數規劃問題;鑒于它是一個類似NP-hard的多維背包問題[9],提出了一種高效、低復雜度的啟發式算法.最后,利用仿真實驗驗證所提算法的性能.結果表明,本文算法能顯著提高系統的能量效率、降低系統的計算復雜度,且其性能接近最優解.

1 系統模型

考慮一個多用戶的中繼網絡,其中的用戶具有不同的速率需求.該網絡包含1個宏基站(BS)、M個中繼、M+1個站點和K個用戶.令和表示所有站點和用戶集合.圖1為系統模型示意圖.圖中,宏基站的覆蓋半徑為RBS,中繼i的覆蓋半徑為Ri.宏基站位于坐標原點,中繼i(1≤i≤M)和用戶k(1≤k≤K)之間的距離為di,k(0≤di,k≤Ri),宏基站和中繼i的距離為dBS,i(0≤dBS,i≤RBS-Ri),宏基站和用戶k的距離為dBS,k(0≤dBS,k≤RBS).網絡中,如果中繼處于工作狀態,則在中繼覆蓋范圍內的用戶既可由宏基站直接為其提供服務,也可通過中繼采用解碼轉發(decode and forward relaying,DFR)的方式為其服務;如果中繼處于休眠狀態,用戶則只能由其相鄰的其他工作站點為其提供服務.本文中，假設宏基站和各個中繼間的干擾已通過某種干擾管理機制去除,站點間共享所有必需的信息.

圖1 系統模型示意圖

1.1 傳播模型

根據3GPP LTE[1]的規定,系統可以分配給每個用戶的最小時頻資源塊(TFRB)是一個包含了12個子載波(頻率為180 kHz)并且持續1個時隙(1 ms)的資源組合.又令NBS和Ni分別表示宏基站和中繼i上每秒可用的TFRB個數.

通過導頻檢測每個用戶可以得到的可測站點的信噪比.用戶k在中繼i中某個TFRB上的接收信噪比Si,k可表示為

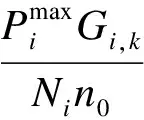
(1)

Qi,k=Wlog2(1+Si,k)

(2)

式中，W為TFRB的大小.

如果用i代替式(1)和(2)中的k,用BS代替i,則式(1)和(2)也可表示中繼i在宏基站中某個TFRB上的信噪比SBS,i和可達速率QBS,i.

1.2 負載模型

網絡必須嚴格保證每個用戶的速率需求.令中繼覆蓋范圍內用戶k的速率需求為rk.用戶k由宏基站直接服務時給宏基站帶來的負載為

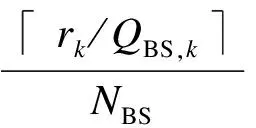
(3)

式中,?rk/QBS,k?表示宏基站分配給用戶k的TFRB個數.

當用戶k通過中繼i采用DFR方式進行通信時,用戶k給系統帶來的負載可分為2個部分.一部分是宏基站將用戶k的數據傳送給中繼i時給宏基站造成的負載ρBS,i,k,即

(4)

另一部分是中繼i將用戶k所需的數據傳送給用戶k時,用戶k給中繼i造成的負載ρi,k,即

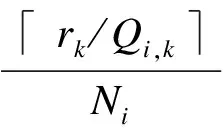
(5)

1.3 能耗模型

(6)

(7)

(8)

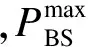
當用戶k通過中繼i采用DFR方式進行通信時,系統要為用戶k消耗的射頻端輸入能耗為

(9)

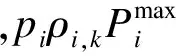
2 問題建模

為了構建基于能量效率的用戶動態接入模型,引入布爾變量xi,k來表示中繼i和用戶k之間的接入關系,即

(10)

如果用BS代替式(10)中的i,則式(10)可表示宏基站和用戶k之間的接入關系.

為了描述中繼的工作狀態,引入指示變量αi表示中繼i的工作模式，即

(11)

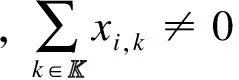
定義網絡中的總輸入能量效率E為

E=

(12)

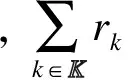
中繼網絡中用戶動態接入的目標是在滿足所有用戶速率需求的前提下最大化系統能量效率.因此,該問題可描述為

maxE

(13)

(14)

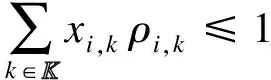
(15)

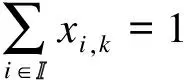
(16)

xi,k∈{0,1} ?i∈，?k∈

(17)

由式(14)可知,用戶接入方案必須保證宏基站的負載不能超過負載限制.式(15)表示用戶接入方案必須滿足各個中繼都不超過負載限制的條件.式(16)表示每個用戶只能接入一個站點.

式(13)～(17)所描述的問題是一個整數優化問題,該問題類似于多維背包問題[9].除了利用窮搜法(exhaustive search,ES)逐個遍歷xi,k的所有組合之外,目前還沒有更有效的方法找到最優解.然而,窮搜法的計算復雜度非常高,隨著用戶數和站點個數的增加呈指數增加.例如,系統中有2個中繼和50個用戶,則窮搜法的復雜度為O((1+M)K)=O((1+2)50)≈7.2×1023.

3 實用算法

3.1 SNRB算法

文獻[11]提出了一種基于信噪比 (signal to noise based,SNRB)的用戶接入算法(簡稱為SNRB算法).該算法中,用戶按照最大信噪比來選擇接入站點.然而,SNRB算法并沒有從能量效率的角度考慮用戶接入問題.例如,如圖1所示,由于中繼2到用戶1的信噪比較宏基站到用戶1的信噪比高,在SNRB算法中用戶1接入中繼2;但是,在保證相同速率需求的前提下,用戶1接入中繼2會消耗部分射頻能耗,故應將其接入宏基站以具有更高的能量效率.相反地,在SNRB算法中,用戶2接入宏基站,若將其接入中繼2中則可提高能量效率,因為宏基站到用戶2的路徑損耗較大.此外,在中繼負載較低時,SNRB算法并沒有采用可以提高能量效率的中繼休眠機制.

3.2 基于能量效率的用戶接入算法

本文提出了一種高效、低復雜度的基于能量效率的用戶接入算法 (user association for energy efficiency maximization,UAEEM).令i為中繼i覆蓋范圍內的用戶集合為用戶k從當前接入站點m到站點n射頻端的能量效率變化情況,其計算公式為

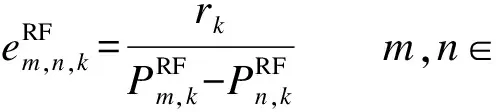
(18)

基于以上定義,UAEEM算法具體描述如下.

算法1UAEEM算法

輸入:當前用戶接入狀態.

輸出:用戶接入狀態和系統能量效率.

③ 在滿足系統負載限制的前提下,按能量效率降低最少的準則,計算中繼i*休眠時將服務用戶切換至相鄰工作站的系統能量效率.如果該能量效率大于步驟②計算得到的系統能量效率,則將i*休眠,并將其用戶切換到相應站點.

④ 重復步驟①～步驟③,直到所有中繼被檢查完畢.

在第1次運行步驟①時,復雜度為M,第2次運行時復雜度為M-1,最后1次運行時復雜度為1,因此步驟①的總復雜度為(M+1)M/2.在步驟②中,每個用戶的最大判決空間為M.在第1次運行步驟②時,要從KM個判決空間中找出第1個用戶,第2次運行時,從(K-1)M中找出第2個用戶.以此類推,最后一次運行時,從M個空間中找出最后1個用戶,因此步驟②的最大復雜度為K·(M+1)M/2.假設系統中所有K個用戶都被檢查了1遍,則步驟③的最大復雜度為KM.因此,該算法將式(13)～(17)描述的問題的總復雜度從O((1+M)K)降低到O(M(KM+3K+M+1)/2).

4 仿真實驗

4.1 仿真設置

本文的路徑損耗計算采用3GPP LTE標準中的大尺度衰落模型[8].宏基站到用戶k的路徑損耗按131.1+42.8lgdBS,k計算,宏基站到中繼i的路徑損耗按125.2+36.3lgdBS,i計算,中繼i到用戶k的路徑損耗按145.4+37.5lgdi,k計算.

本文中能耗模型的參數設置參照EARTH項目中的能耗模型(見表1)[10]. 表1中,Pmax為站點的射頻端最大發射功率;p為站點的功放效率;P0為站點空載時的最小射頻能耗;PS為站點休眠時所需的最小系統能耗.

表1 EARTH能耗模型參數設置

4.2 實驗結果

在中繼覆蓋范圍不重疊和重疊2種場景下,對MBSO算法、SNRB算法、UAEEM算法和ES算法的性能進行比較. 任意多中繼場景都可以由2個中繼覆蓋范圍不重疊或者重疊的場景組成,因此,為簡單起見,假設中繼網絡中有2個中繼.假設在中繼覆蓋范圍不重疊和重疊的場景中,這2個中繼之間的距離分別為600和300 m.隨機選取1 000次仿真實驗結果,取平均值,即可得到這4種算法的平均性能.圖2給出了UAEEM算法和窮搜算法的能量效率比值的累積分布值圖.為檢驗不同用戶初始接入狀態對UAEEM算法的影響,用UAEEM-MBSO和UAEEM-SNRB分別表示UAEEM算法中的用戶初始接入狀態為采用MBSO和SNRB算法得到的用戶初始接入狀態.圖2中,橫坐標e表示采用UAEEM算法和ES算法得到的能量效率比值；縱坐標c表示能量效率比值的累積分布值.由于計算機的計算能量有限,選取用戶數為20,用戶平均速率需求為320 kbit/s.由圖2可知,UAEEM算法無論在哪種初始狀態下都能很好地逼近窮搜算法.此外,中繼覆蓋范圍重疊場景下該算法的性能有所下降,這是因為中繼覆蓋范圍重疊會造成可行解范圍擴大,UAEEM算法落入局部最優解的可能性變大.

圖2 UAEEM算法和窮搜算法的能量效率比

圖3給出了4種算法的能量效率隨用戶平均速率需求變化的情況.該場景下的用戶數為50個,用戶平均速率需求為320 kbit/s.由圖3(a)可知,隨著系統中用戶速率需求的增加,UAEEM算法和SNRB算法的能量效率明顯提高,而MBSO算法則沒有變化.究其原因在于,MBSO算法中中繼一直處于休眠狀態,其能量效率模型是一個線性模型;而在UAEEM算法和SNRB算法中,中繼發揮了提高射頻端能量效率的作用.在用戶平均速率需求較低時,SNRB算法中的中繼在射頻端的能量效率提高不足以彌補工作帶來的電路端能量效率損失,故其能量效率最差. 對于綜合考慮射頻端和電路能量效率的UAEEM算法而言,在用戶速率需求較低時它能讓中繼休眠,速率需求較高時則能更有效地將用戶接入相應站點,故其能量效率總是最優的.由圖3(b)可知,中繼覆蓋范圍重疊場景下,當用戶平均速率需求較高時SNRB算法的性能有所提高;這是因為SNRB算法中某些用戶可切換的站點增加,不僅可以切換到宏基站,還可能切換到具有更高能量效率的相鄰中繼.

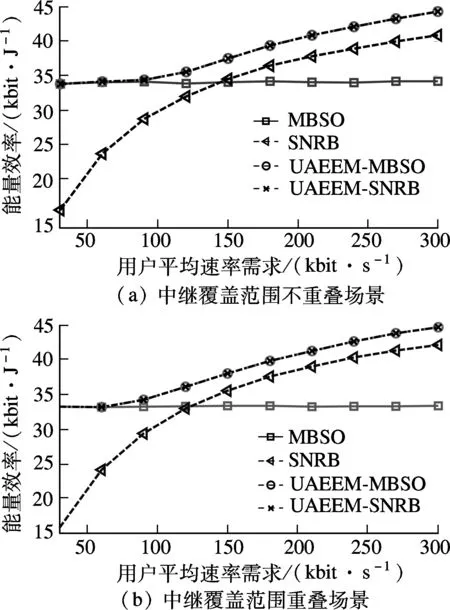
圖3 能量效率與用戶平均速率需求的關系

初始用戶接入狀態的不同并不影響UAEEM算法的結果.分別運行SNRB算法和UAEEM-MBSO算法10次，并將運行后得到的10次獨立用戶接入狀態分布快照進行疊加，所得的用戶接入狀態分布圖見圖4.每次快照的用戶數為50,用戶平均速率需求為320 kbit/s.由圖可知,UAEEM算法可將離宏基站較近的用戶接入宏基站,將離宏基站較遠的用戶接入相應的中繼中,從而更有效地利用系統資源提高能量效率.

圖4 用戶接入狀態分布圖

5 結語

本文研究了中繼網絡中基于能量效率的用戶動態接入問題.首先,將用戶數據需求嚴格受限下基于能量效率最優的用戶動態接入問題建模為一個整數優化問題,并分析其最優解復雜度;然后,提出了一種高效、低復雜度的UAEEM算法,該算法根據用戶接入不同站點的能量效率來判斷用戶歸屬.最后,進行仿真實驗.實驗結果表明,該算法能顯著提高系統的能量效率,且其性能接近最優解.

)

[1] 3GPP. TR 36.814v1.5.0 further advancements for E-UTRA physical layer aspects(release 9)[S/OL]. (2009)[2012-11-25].http://www.3gpp.org/ftp/Specs/archive/36_series/36.814/.

[2] Madan R,Metha N,Molisch A,et al. Energy-efficient cooperative relaying over fading channels with simple relay selection[J].IEEETransactionWirelessCommunication,2008,7(8): 3013-3025.

[3] Zhou Z,Zhou S,Cui J H,et al. Energy efficient cooperative communication based on power control and selective single relay in wireless sensor networks [J].IEEETransactionWirelessCommunications,2008,7(8): 3066-3078.

[4] Fantini R,Sabella D,Caretti M. An E3F based assessment of energy efficiency of relay nodes in lte-advanced networks [C]//Proceedingsofthe22ndInternationalSymposiumonPersonalIndoorandMobileRadioCommunications. Toronto,Canada,2011: 182-186.

[5] Marsan M,Chiaraviglio L,Ciullo D,et al. Optimal energy savings in cellular access networks [C]//Proceedingsof2009IEEEInternationalConferenceonCommunicationsWorkshop. Dresden,Germany,2009: 1-5.

[6] Gong J,Zhou S,Niu Z. A dynamic programming approach for base station sleeping in cellular networks [J].IEICETransactiononCommunications,2012,E95-B(2): 551-562.

[7] Zhou S,Goldsmith A,Niu Z. On optimal relay placement and sleep control to improve energy efficiency in cellular networks [C]//Proceedingsof2011IEEEInternationalConferenceonCommunications. Kyoto,Japan,2011: 1-6.

[8] Li X,Wang H,Liu N,et al. Dynamic user association for energy minimization in macro-relay network [C]//Proceedingsof2012IEEEWirelessCommunicationsandSignalProcessing. Huangshan,China,2012: 187-196.

[9] Martello S,Toth P.Knapsackproblems:algorithmsandcomputerimplementation[M]. London,UK: Chichester,1990.

[10] Auer G,Blume O,Giannini V,et al. Energy efficiency analysis of the reference systems,areas of improvements and target breakdown [EB/OL].(2012-01-31)[2012-11-20]. https://bscw.ict-earth.eu/pub/bscw.cgi/d71252/EARTH_WP2_D2.3_v2.pdf.

[11] Hu H,Liu H. Range extension without capacity penalty in cellular networks with digital fixed relays[C]//Proceedingsof2004IEEEGlobalTelecommunicationConference. Dallas,Texas,USA,2004: 3053-3257.