DH36鋼拉伸塑性流動特性及本構關系＊

孟衛華，郭偉國，王建軍，孔德栓

（西北工業大學航空學院，陜西 西安710072）

在某個溫度范圍中金屬塑性流動應力隨溫度增加而增大，峰值在溫度軸上呈現似鐘形，被稱為第三型應變時效現象［1］，其機理可歸于溶質原子氣團與位錯相互作用的結果［2－4］，在形式上與靜態應變時效和Portevin－Lechatelier型動態應變時效有區別。N.S.Nemat等［5］對壓縮加載下DH36鋼塑性流動行為進行研究表明第三型應變時效現象導致塑性流動本構關系建立困難，本構模型中也不包含“第三型應變時效現象”部分的應力預測。為了更深入理解DH36鋼的塑性流動行為，本文中對拉伸加載下DH36鋼的拉伸塑性流動特性進行實驗研究，驗證在拉伸加載下第三型應變時效現象的存在，并通過端口形貌圖對變形前后試樣的微觀結構進行觀測，探討時效產生的原因，最后基于文獻［5］中模型框架，發展包含第三型應變時效的物理概念統一本構模型，并與實驗結果進行比較，驗證該模型能夠較好的預測DH36鋼的塑性拉伸流動應力。

1 實驗過程及結果

在應變率為0.001和0.1s－1下，采用CSS4410型萬能材料實驗機進行拉伸加載實驗。在293～800K溫度下，高溫實驗由自主設計的加熱爐和溫度反饋儀控制得到，每個溫度下保溫5min后再對試樣加載，使試樣溫度誤差控制在±5K。

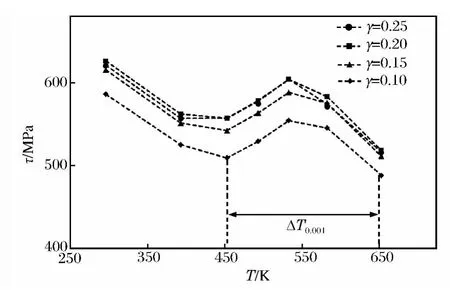
圖1 0.001s－1應變率下流動應力與溫度的關系Fig.1 Flow stress varied with temperature at the strain rate of 0.001s－1

圖1所示為不同應變率下DH36鋼流動應力與溫度關系。由圖1可知在應變率0.001s－1加載條件下，當溫度從293K升高到450K時，流動應力迅速下降；但當溫度從450K到660K（圖1中所示的ΔT0.001時效區），流動應力先逐漸增加到峰值，對應溫度TSA約550K，然后逐漸下降。

當應變率提高到0.1s－1時，與應變率0.001s－1加載下類似，流動應力隨應變率增加而增加，如圖2所示。應力峰值τSA所對應溫度TSA移至更高溫度約620K，時效溫度區移到更高溫度范圍480～730K（圖2中所示的ΔT0.1時效區）。這種流動應力在溫度軸上所出現的鐘形現象，被稱為第三型應變時效現象［1］。

圖2 0.1s－1應變率下流動應力與溫度的關系Fig.2 Flow stress varied with temperature at the strain rate of 0.1s－1

2 微觀斷口分析

將變形試樣沿加載軸方向剖開，經研磨拋光，并用3mL硝酸和97mL的酒精溶液作為腐蝕液對試樣腐蝕，采用IEISS SUPRATM55電子掃描顯微鏡對拉伸變形試樣以及斷口進行微觀分析。

圖3 不同溫度下DH36鋼斷口形貌圖Fig.3 SEM fractorgraphy of DH36steel at different temperatures

圖3中給出了DH36鋼在應變率為0.1s－1、不同溫度下的拉伸斷口形貌照片。由圖3可看出，在溫度為293K時，試樣斷面比較平齊，基本是細小的韌窩區，斷口為準解理斷裂特征；在溫度為523K時，斷面出現大小不同且較為明顯韌窩，韌窩周圍有小的解理面，即以韌性斷裂為主，以準解理和韌窩混合斷裂為特征；在溫度為653K時，出現典型的韌窩形貌，大韌窩包含著若干小韌窩，個別韌窩區存在微小的孔洞。綜上可以發現，隨著溫度升高，斷面韌窩數量增多，韌窩變大。

圖4所示為變形試樣金相照片，在293、453和523K溫度下，微觀照片上僅有很少孔洞在晶界或晶內出現。在653K時，晶界處和晶體內出現了大量的孔洞，孔洞的形成和擴展是微孔聚集斷裂的典型標志，圖中大量微小孔洞在晶界或晶內分布，意味著裂紋可在晶界或在晶體內部形成，而孔洞擴展聚合可最終導致斷裂。從523 K時的金相圖（圖4（c））發現：晶界和晶粒中有大量第二相析出，第二相的析出可提高合金的中溫強度［6］。均勻細小的第二相顆粒在產生強化作用的同時并不損害鋼材的塑性。因此，第三型應變時效的發生可能與合金晶界和晶粒中大量的第二相析出強化作用有關。

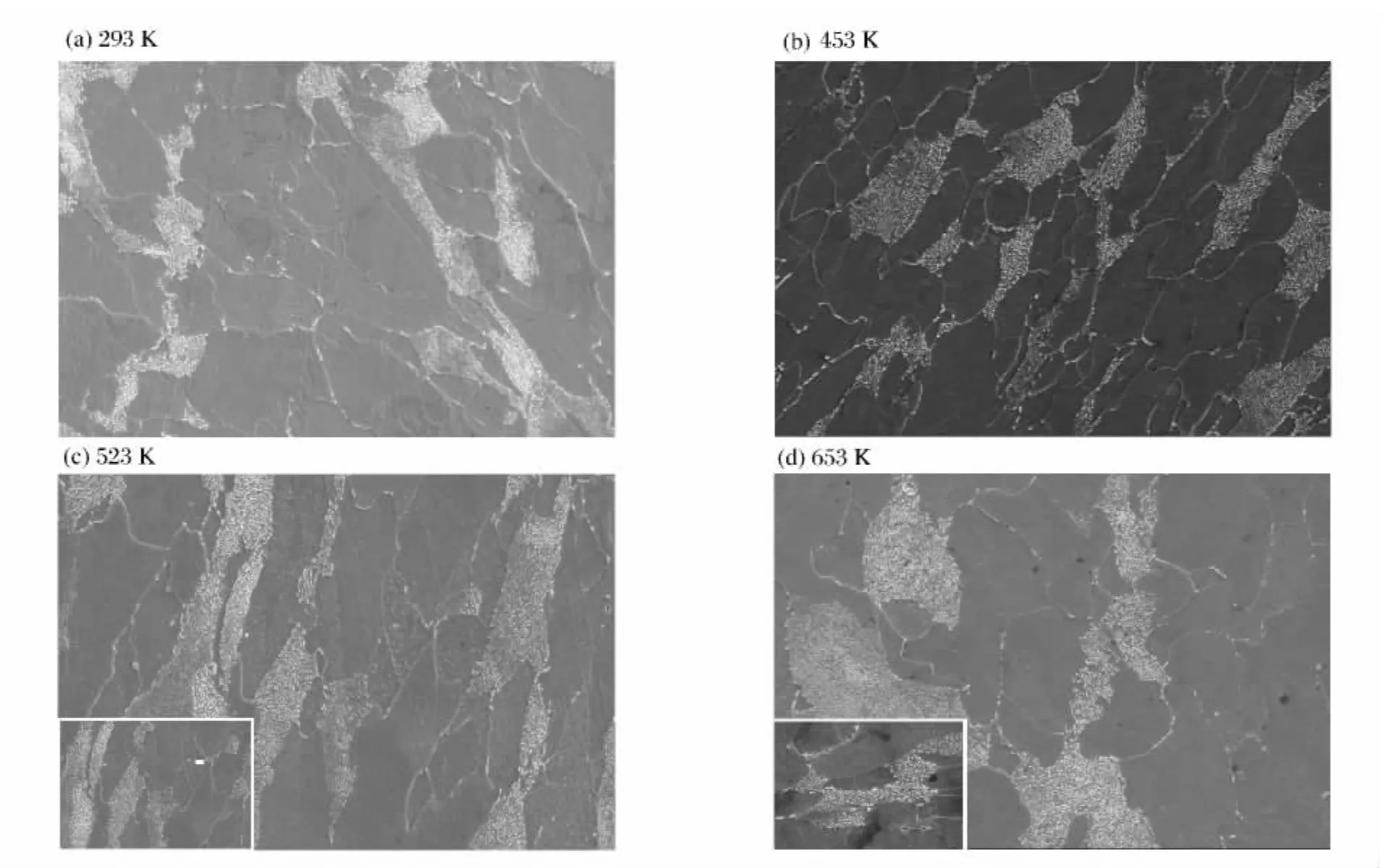
圖4 不同溫度下DH36鋼變形試樣金相照片Fig.4 The Metallograph of DH36steel at different temperatures

3 統一本構關系

N.S.Nemat等［5］已對金屬塑性流動的熱激活應力τ＊（γ，γ，T）與溫度T 和應變率γ之間建立了完善的物理概念本構關系，但此本構關系不能描述第三型應變時效。若考慮動態應變時效現象［5，7］，可認為流動應力由3個部分疊加而成，分別為：熱激活部分τ＊（γ，γ，T）、非熱部分τ（α）（γ）和第三型應變時效部分τSA（γ，γ，T），即：

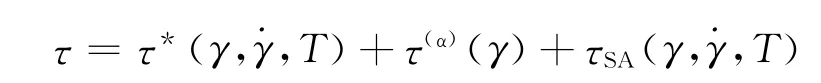
圖5（a）所示為由非熱部分τα（γ）的實驗散點擬合出的本構關系曲線，圖5（b）所示為由熱激活部分τ＊（γ，γ，T）的實驗散點擬合出的本構關系曲線，圖5（c）所示為第三型應變時效部分τSA（γ，γ，T）的實驗散點擬合出的本構關系曲線，圖5（d）為3個部分累加得到的DH36鋼在0.1s－1應變率下的流動應力。

根據圖1～2和圖5（c）可知DH36鋼在拉伸條件下的第三型應變時效部分流動應力與溫度、應變率的變化規律以及在時效區表現出來的力學行為具有以TSA溫度為中心的近似對稱性，因此可尋找具有對稱性（近似對稱性）的方程來描述此第三型應變時效部分流動應力

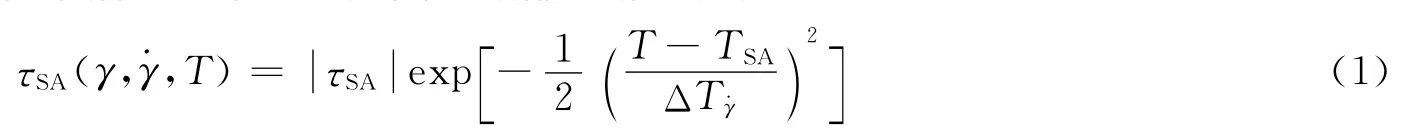
綜合熱激活部分τ＊（γ，γ，T）、非熱部分τ（α）（γ）以及第三型應變時效部分流動應力τSA得到如下塑性流動本構方程

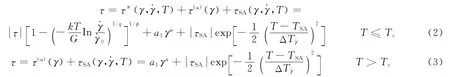
式中：T＝T0＋T（η），T0為參考溫度，一般取室溫，T（η）為塑性變形導致的溫升，準靜態：T（η）≈0，高應變率為閾值剪切應力，表示超過此應力，溶質原子氣團不需要熱激活錯位就可以越過障礙運動；k為Boltzmann常數，G為吉布斯自由能；0＜p≤1和1＜q≤2是對短程障礙構型的描述；系數a1、指數n描述非熱流動應力特性；DH36鋼密度ρ＝7.8g／cm3，質量定容熱容cV≈0.5J／（g·K）。

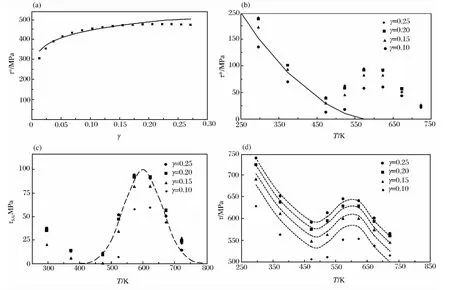
圖5 DH36鋼在應變率0.1s－1下的流動應力實驗結果Fig.5 Experimental results of flow stress for DH36steel at the strain rate of 0.1s－1

依據式（2）～（3）對DH36鋼在0.1s－1應變率下進行塑性流動應力預測，本構模型與實驗結果在0.1s－1應變率下吻合較好，如圖5（d）所示。

為獲得DH36鋼在0.001和0.1s－1應變率下的統一本構方程，根據DH36鋼在此應變率范圍內動態應變時效與溫度、應變率和應變的變化規律，并結合式（1），通過計算分析，最終確定式（1）中TSA和ΔTγ的具體關系分別為：

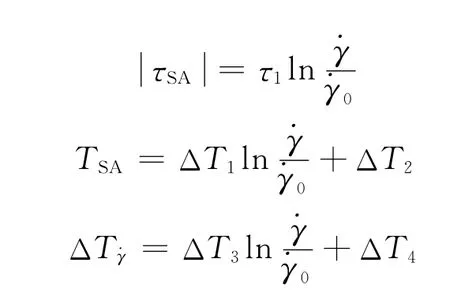
式中：τ1描述的是第三型應變時效流動應力特性，ΔT1、ΔT2、ΔT3和ΔT4分別描述的是不同應變率下第三型應變時效的峰值應力對應的溫度和時效溫度區域的寬度。

通過對統一本構模型和DH36鋼試驗數據進行最小二乘法擬合可得本構模型的各個參數1 000MPa，k／G＝6.6×10－5K－1，γ0＝2×1010s－1，p＝2／3，q＝2，a1＝680MPa，n＝0.12，τ1＝－3.5MPa，ΔT1＝13K，ΔT2＝940K，ΔT3＝2K，ΔT4＝110K。

綜上可得，非熱部分τ（α）（γ）的具體表達式為：

熱激活部分為：

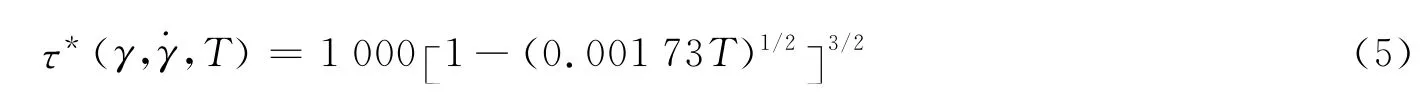
根據表現出來的力學行為具有近似對稱性，確定第三型應變時效部分為：

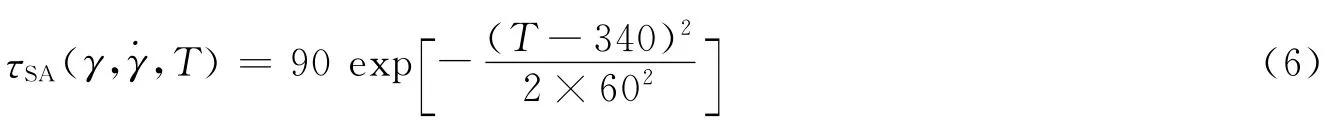
圖6中給出了DH36鋼在不同溫度下統一本構模型預測結果與拉伸加載實驗結果的對比，可知統一本構模型預測結果與實驗結果吻合較好。

圖6 DH36鋼的統一本構模型預測與實驗結果對比Fig.6 Comparison between unified constitutive model predictions and experimental results for DH36steel

4 結 論

通過對DH36鋼在應變率0.001和0.1s－1下、溫度從293～800K的拉伸塑性流動應力進行實驗，得出的主要結論為如下：

（1）在293～800K溫度范圍，0.001和0.1s－1應變率下，第三型應變時效現象出現，隨應變率的增加，時效發生的溫度區域右移，移向更高溫度；

（2）第三型應變時效的發生可能與DH36鋼在中溫區晶界和晶體內大量的第二相析出產生的強化作用有關聯；

（3）建立的包含第三型應變時效的統一本構模型可以較好預測DH36鋼塑性流動應力。

［1］Guo Wei－guo.Dynamic strain aging during the plastic flow of metals［J］.Key Engineering Materials，2007，340／341：823－828.

［2］Kubin L P，Estrin Y，Perrier C.On static strain ageing［J］.Acta Metallurgica et Materialia，1992，40（5）：1037－1044.

［3］Klose F B，Ziegenbein A，Weidenmuller J，et al.Portevin－Lechatelier effect in strain and stress controlled tensile tests［J］.Computational Materials Science，2003，26：80－86.

［4］錢匡武，李效琦，蕭林鋼，等.金屬和合金中的動態應變時效現象［J］.福州大學學報：自然科學版，2001，29：8－23.Qian Kuang－wu，Li Xiao－qi，Xiao Lin－gang，et al.Dynamic strain aging phenomenon in metals and alloys［J］.Journal of Fuzhou University：Natural Science，2001，29：8－23.

［5］Nemat N S，Guo Wei－guo.Thermomechanical response of DH36structural steel over a wide range of strain rates and temperatures［J］.Mechanics of Materials，2003，35（11）：1023－1047.

［6］張偉.第二相方向性析出和晶粒細化提高FeMnSiCrNi基合金記憶效應的研究［D］.成都：四川大學，2007.

［7］孟衛華，郭偉國，蘇靜，等.DH36鋼的塑性流動統一本構關系研究［J］.力學學報，2011，43（5）：954－962.Meng Wei－hua，Guo Wei－guo，Su Jing，et al.Study of plastic flow unified constitutive relation for steel DH36［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43（5）：954－962.